Multinomial distribution နိဒါန်း

ရလဒ်တစ်ခုစီသည် ပုံသေ ဖြစ်နိုင်ခြေရှိသည့် k မတူညီသောရလဒ်များအတွက် တိကျသောရေတွက်မှုအရေအတွက်တစ်ခုရရှိရန် ဖြစ်နိုင်ခြေကို ဖော်ပြသည်။

_{ကျပန်း} variable _{_} ကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင် _{လျှင်} –

ဖြစ်နိုင်ခြေ = n * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

ရွှေ-

• n- ဖြစ်ရပ်စုစုပေါင်း
• x ₁ : ရလဒ် 1 ဖြစ်ပေါ်သည့် အကြိမ်အရေအတွက်
• p ₁ : ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် ရလဒ် 1 သည် ဖြစ်နိုင်ခြေရှိသည်။

ဥပမာအားဖြင့်၊ အိုးထဲတွင် အနီရောင် စကျင်ကျောက် ၅ လုံး၊ အစိမ်းရောင် စကျင်ကျောက် ၃ လုံးနှင့် အပြာရောင် စကျင်ကျောက် ၂ လုံး ရှိသည် ဆိုပါစို့။ အကယ်၍ ကျွန်ုပ်တို့သည် ဂူထဲမှ စကျင်ကျောက် ၅ ခုကို ကျပန်းဆွဲထုတ်ပြီး အစားထိုးပါက၊ အနီရောင် စကျင်ကျောက် ၂ လုံး၊ အစိမ်းရောင် စကျင်ကျောက် ၂ လုံး နှင့် အပြာရောင် စကျင်ကျောက် ၁ လုံး ရရှိရန် ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

ဤမေးခွန်းကိုဖြေဆိုရန်၊ ကျွန်ုပ်တို့သည် အောက်ဖော်ပြပါ ကန့်သတ်ချက်များဖြင့် အမျိုးမျိုးသော ဖြန့်ဖြူးမှုကို အသုံးပြုနိုင်ပါသည်။

• n : ၅
• x ₁ (# အနီရောင် စကျင်ကျောက်များ) = 2၊ x ₂ (# အစိမ်းရောင် စကျင်ကျောက်များ) = 2၊ x ₃ (# အပြာရောင် စကျင်ကျောက်များ) = 1
• p ₁ (အနီရောင် prob.) = 0.5၊ p ₂ (အစိမ်းရောင် prob.) = 0.3၊ p ₃ (အပြာရောင် prob.) = 0.2

ဤဂဏန်းများကို ဖော်မြူလာထဲသို့ ပေါင်းထည့်ခြင်းဖြင့် ဖြစ်နိုင်ခြေသည်-

ဖြစ်နိုင်ခြေ = 5 * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0.135 ။

Multinomial Distribution Practice ပြဿနာများ

အမည်ပေါင်းများစွာ ဖြန့်ဖြူးခြင်းဆိုင်ရာ သင်၏အသိပညာကို စမ်းသပ်ရန် အောက်ပါအလေ့အကျင့်ပြဿနာများကို အသုံးပြုပါ။

မှတ်ချက်- ဤမေးခွန်းများအတွက် အဖြေများကို တွက်ချက်ရန် Multinomial Distribution Calculator ကို အသုံးပြုပါမည်။

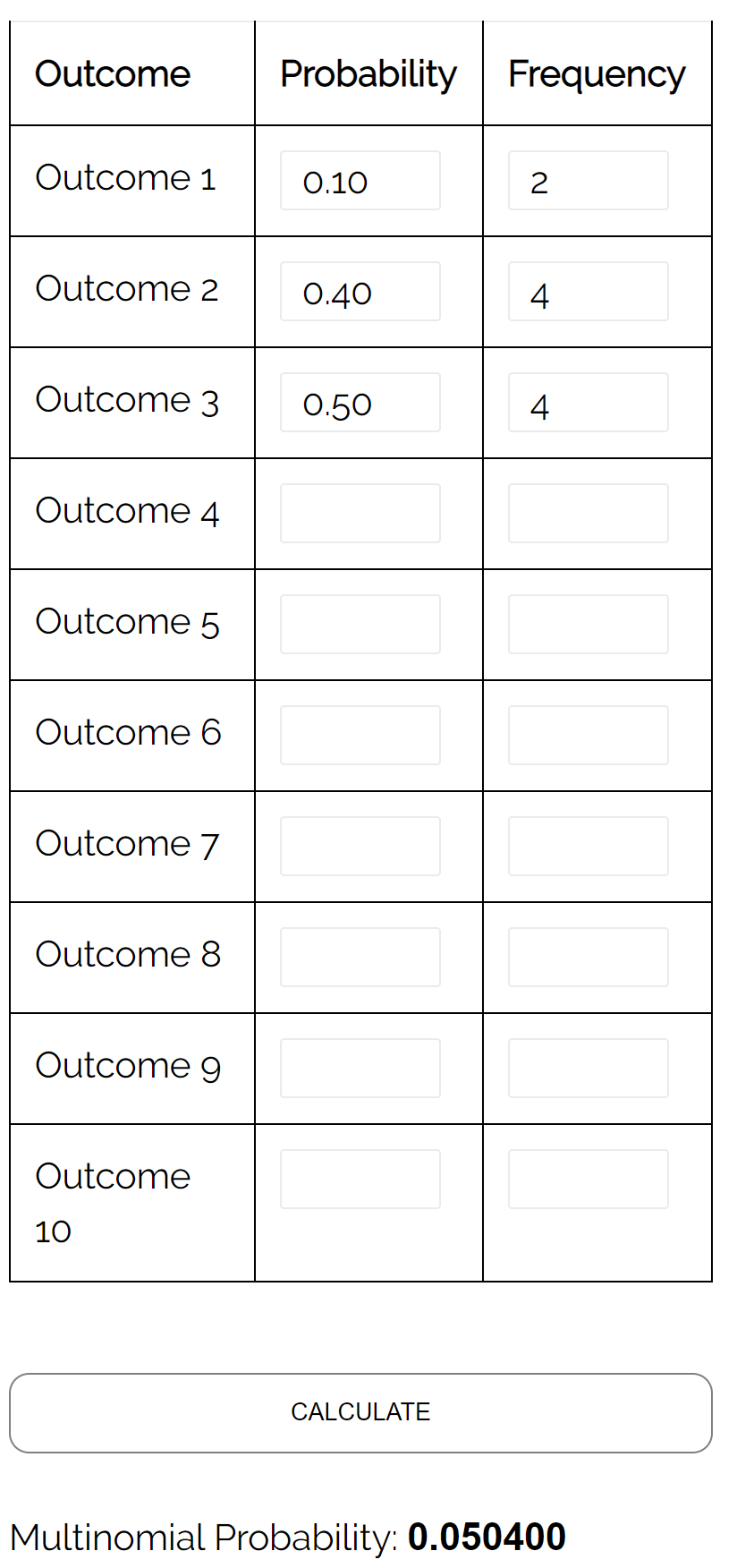
ပြဿနာ ၁

မေးခွန်း- မြို့တော်ဝန်အတွက် သုံးမျိုး ရွေးကောက်ပွဲတွင် ကိုယ်စားလှယ်လောင်း A က ဆန္ဒမဲ ၁၀ ရာခိုင်နှုန်း၊ ကိုယ်စားလှယ်လောင်း B က ဆန္ဒမဲ ၄၀ ရာခိုင်နှုန်း ရရှိပြီး ကိုယ်စားလှယ် C က မဲ ၅၀ ရာခိုင်နှုန်း ရရှိသည်။ အကယ်၍ ကျွန်ုပ်တို့သည် မဲဆန္ဒရှင် ၁၀ ဦး၏ ကျပန်းနမူနာကို ရွေးချယ်ပါက၊ ကိုယ်စားလှယ်လောင်း A ကို ၂ ဦးက မဲပေးခဲ့ပြီး ကိုယ်စားလှယ်လောင်း B အတွက် ၄ ဦးက မဲပေးခဲ့ပြီး ကိုယ်စားလှယ်လောင်း C အတွက် ၄ ဦးက မဲပေးခဲ့ခြင်း ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

အဖြေ- အောက်ဖော်ပြပါ ထည့်သွင်းမှုများဖြင့် Multinomial Distribution Calculator ကို အသုံးပြုခြင်းဖြင့် ဖြစ်နိုင်ခြေမှာ 0.0504 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့ရှိရပါသည်။

ပြဿနာ ၂

မေးခွန်း- ကြွက်တွင်းတစ်ခုတွင် အဝါရောင်စကျင်ကျောက် ၆ လုံး၊ အနီရောင်စကျင်ကျောက် ၂ လုံးနှင့် ပန်းရောင်စကျင်ကျောက် ၂ လုံးပါရှိသည်ဆိုပါစို့။ အကယ်၍ ကျွန်ုပ်တို့သည် အိုးထဲမှ ဘောလုံး ၄ လုံးကို ကျပန်း အစားထိုး၍ အစားထိုးပါက၊ ဘောလုံး ၄ လုံးစလုံး အဝါရောင်ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။

အဖြေ- အောက်ဖော်ပြပါ ထည့်သွင်းမှုများဖြင့် Multinomial Distribution Calculator ကို အသုံးပြုခြင်းဖြင့် ဖြစ်နိုင်ခြေမှာ 0.1296 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့ရှိရပါသည်။

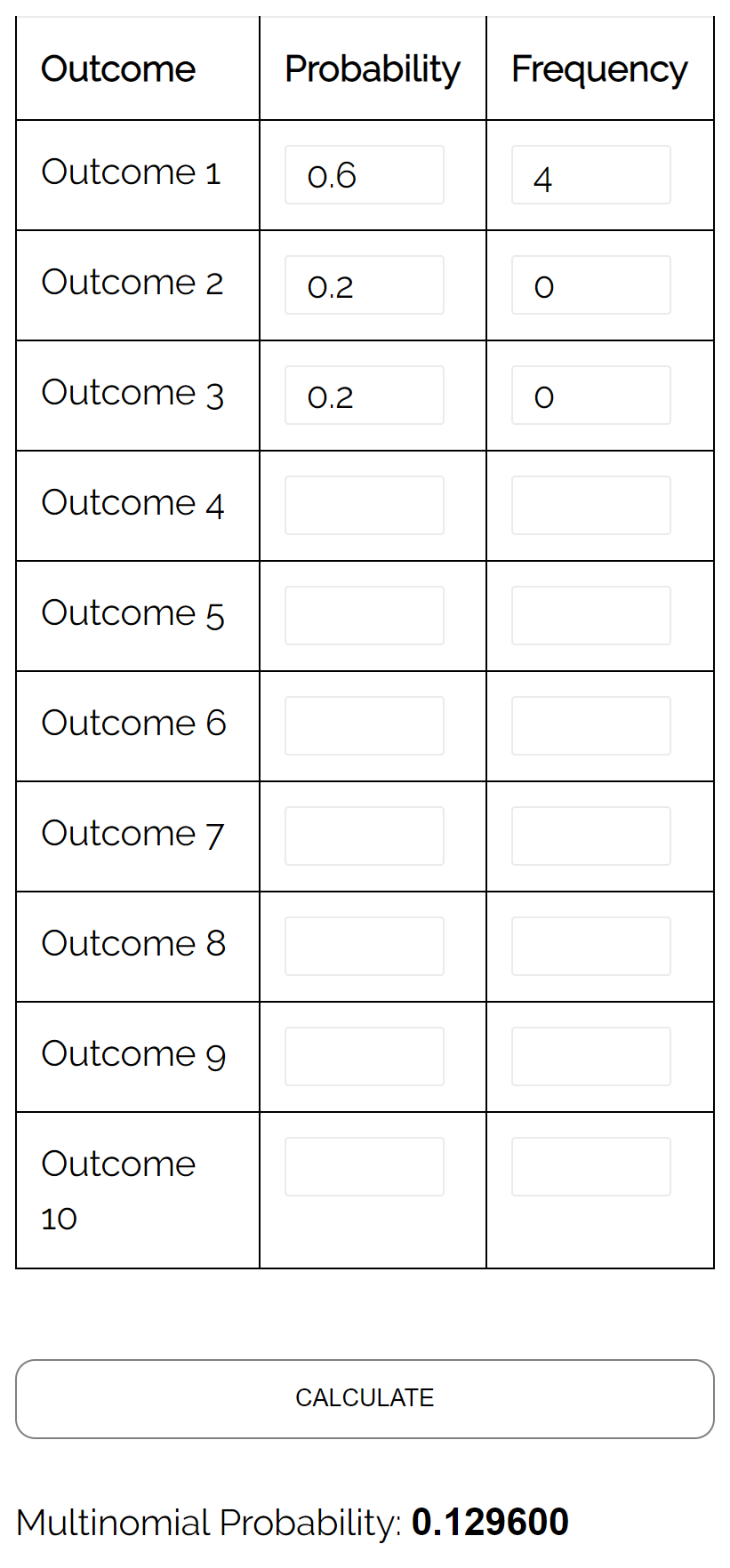
ပြဿနာ ၃

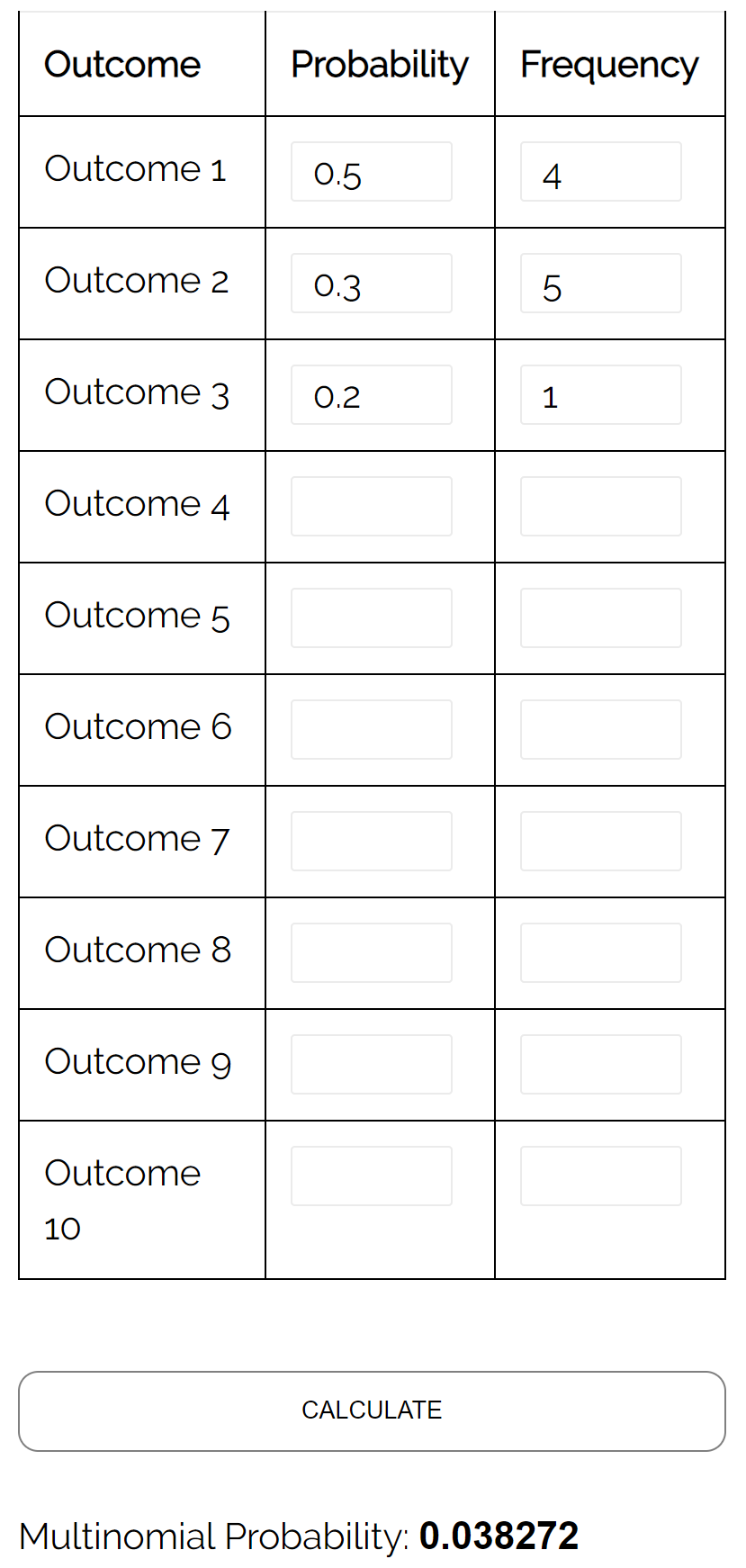
မေးခွန်း- ကျောင်းသားနှစ်ယောက် တစ်ယောက်ကိုတစ်ယောက် စစ်တုရင်ကစားနေတယ်ဆိုပါစို့။ ပေးထားသည့်ဂိမ်းတစ်ခုတွင် ကျောင်းသား A နိုင်နိုင်ခြေ ဖြစ်နိုင်ခြေမှာ 0.5 ဖြစ်ပြီး ကျောင်းသား B က ပေးထားသည့်ဂိမ်းတစ်ခု အနိုင်ရနိုင်ခြေမှာ 0.3 ဖြစ်ပြီး ပေးထားသည့်ဂိမ်းတွင် သရေဖြစ်နိုင်ခြေမှာ 0၊ 2 ဖြစ်သည်။ အကယ်၍ ၎င်းတို့သည် ဂိမ်း 10 ခု ကစားပါက အဘယ်နည်း။ ကစားသမား A က 4 ကြိမ် ၊ ကစားသမား B က 5 ကြိမ် ၊ သူတို့ 1 ကြိမ် သရေဖြစ်နိုင်ခြေ ?

အဖြေ- အောက်ဖော်ပြပါ ထည့်သွင်းမှုများဖြင့် Multinomial Distribution Calculator ကို အသုံးပြုခြင်းဖြင့် ဖြစ်နိုင်ခြေသည် 0.038272 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့ရှိရပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ကိန်းဂဏန်းစာရင်းအင်းဆိုင်ရာ အခြားသော ဘုံဖြန့်ဝေမှုများကို နိဒါန်းပေးသည်-

သာမာန်ဖြန့်ဖြူးမှုမိတ်ဆက်
binomial ဖြန့်ဖြူးခြင်းအကြောင်း နိဒါန်း
Poisson ဖြန့်ဖြူးမှုမိတ်ဆက်
ဂျီဩမေတြီ ဖြန့်ဖြူးမှု မိတ်ဆက်