ကွဲလွဲမှု မက်ထရစ်

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် coariance matrix သည် အဘယ်အရာနှင့် ၎င်း၏ဖော်မြူလာဖြစ်သည်ကို ရှင်းပြထားသည်။ ခိုင်မာသောဥပမာတစ်ခုနှင့် ကွာဟမှုမက်ထရစ်များ၏ ဂုဏ်သတ္တိများဖြင့် ကာဗာမထရစ်ကို မည်သို့ဖန်တီးရမည်ကို သင်တွေ့ရှိလိမ့်မည်။

ကွဲလွဲမှုမက်ထရစ်ဆိုတာ ဘာလဲ။

covariance matrix သည် လေ့လာထားသော variable များ၏ ကွဲလွဲချက်များနှင့် ကွဲလွဲမှုများဖြစ်ပြီး ဒြပ်စင်များဖြစ်သော square matrix တစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ covariance matrix ၏အဓိကထောင့်ဖြတ်၏ဒြပ်စင်များသည် variable တစ်ခုစီ၏ကွဲလွဲမှုဖြစ်ပြီး ကျန်ဒြပ်စင်များသည် variable များကြားရှိကွဲလွဲမှုများဖြစ်သည်။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ covariance matrix ကို နှစ်ခု သို့မဟုတ် ထို့ထက်မကသောကျပန်းကိန်းရှင်များကြားဆက်ဆံရေးကိုခွဲခြမ်းစိတ်ဖြာရန်အသုံးပြုသည်။ covariance matrix သည် များစွာသော variables များကြားဆက်စပ်မှုကို လျင်မြန်စွာအဓိပ္ပာယ်ပြန်ဆိုနိုင်စေသောကြောင့်၊ variables များ၏ တူညီမှုအားလုံး၏တန်ဖိုးများကို တစ်ချိန်တည်းတွင်မြင်နိုင်သောကြောင့်၊ covariance matrix သည် အလွန်အသုံးဝင်ပါသည်။

မျဥ်းမထရစ်အတွက် သင်္ကေတသည် ဂရိအက္ခရာ sigma (Σ) ၏ မြို့တော်ဖြစ်သည်။

ကွဲလွဲမှု မက်ထရစ်ကို ဘယ်လို တွက်မလဲ။

ကိန်းဂဏန်းကိန်းရှင်များစွာ၏ ကွဲလွဲမှုမက်ထရစ်ကို တွက်ချက် ရန်၊ အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

ကိန်းရှင်အားလုံး၏ ကွဲလွဲမှုများကို တွက်ချက်ပါ။
ကိန်းရှင်တစ်စုံစီ၏ ကွဲလွဲမှုကို တွက်ချက်ပါ။
ကွဲလွဲမှု မက်ထရစ်ကို ပုံဖော်ပါ-

variable ၏ကွဲလွဲမှုကို i သည် matrix ၏ အဓိကထောင့်ဖြတ်ပေါ်တွင် ထားရှိရမည်ဖြစ်ပြီး i,i အနေအထားတွင် ပိုမိုတိကျသည်။
ကိန်းရှင် i နှင့် j အကြား ကွဲလွဲမှုကို matrix ၏ i၊j တွင် ထည့်သွင်းရပါမည်။

ထို့ကြောင့် covariance matrix အတွက်ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည် ။

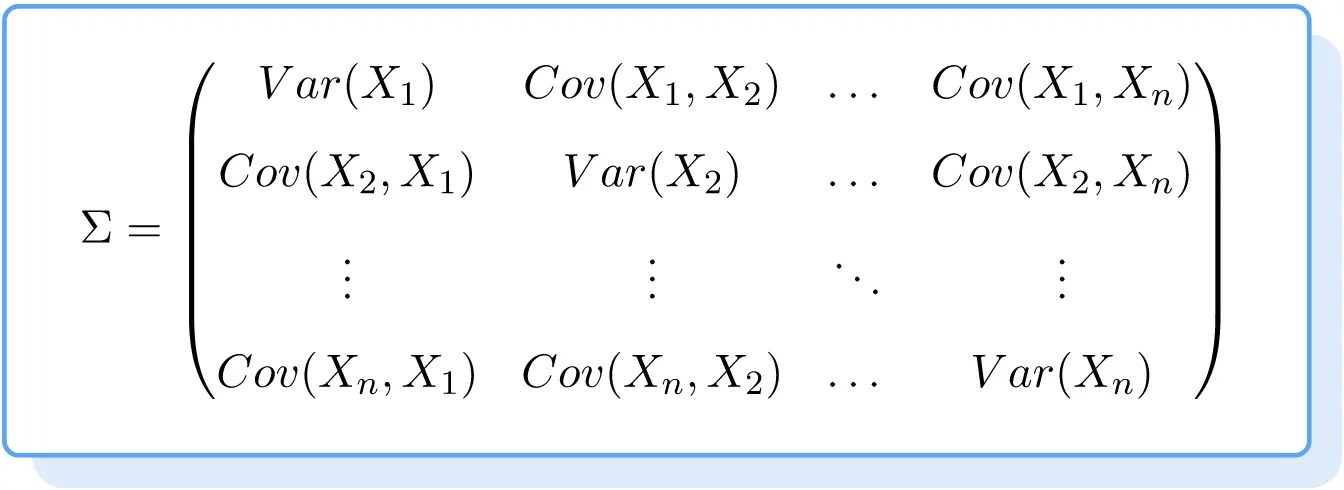
Covariance Matrix ဥပမာ

covariance matrix ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ကြည့်ပြီးနောက်၊ အောက်တွင် အဆင့်ဆင့်သော လေ့ကျင့်ခန်းတစ်ခုဖြစ်ပြီး ဤ matrix အမျိုးအစားကို မည်သို့ဖန်တီးထားသည်ကို သင်ကြည့်ရှုနိုင်ပါသည်။

ကိန်းရှင်များ X၊ Y နှင့် Z တို့၏ ကွဲလွဲမှု matrix ကို တွက်ချက်ပြီး တန်ဖိုးများမှာ-

X: 4၊ 7၊ 12၊ 5၊ 7
နှင့်- ၉၊ ၁၅၊ ၁၉၊ ၆၊ ၈
Z: 7၊ 2၊ 4၊ 6၊ 3

ပထမဦးစွာ ကျွန်ုပ်တို့လုပ်ဆောင်ရန်မှာ ကိန်းရှင်အားလုံး၏ ကွဲလွဲမှုများကို ဆုံးဖြတ်ရန်ဖြစ်သည်-

$Var(X)=7,6$

$Var(Y)=23,44$

$Var(Z)=3,44$

➤ ကွာဟချက်ဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ဒုတိယ၊ ကိန်းရှင်အတွဲတစ်ခုစီကြား ကွဲလွဲမှုကို ကျွန်ုပ်တို့ တွေ့ရှိသည်-

$Cov(X,Y)=11,2$

$Cov(X,Z)=-2,6$

$Cov(Y,Z)=-4,36$

➤ ကွဲပြားမှုဂဏန်းတွက်စက်ကို ကြည့်ပါ။

ကွဲလွဲမှုနှင့် ကွဲလွဲမှုအားလုံးကို ကျွန်ုပ်တို့တွက်ချက်ပြီးသည်နှင့် ကျန်အရာအားလုံးသည် ကွဲပြားမှုမက်ထရစ်ကို ပြုလုပ်ရန်ဖြစ်သည်။ ဒါကိုလုပ်ဖို့၊ ကျွန်ုပ်တို့သည် matrix ၏ ပင်မထောင့်ဖြတ်တွင် ကွဲလွဲမှုတန်ဖိုးများကို ၎င်းတို့၏ သက်ဆိုင်ရာ အနေအထားတွင် ထားရှိသည်-

$\Sigma=\begin{pmatrix}Var(X)&Cov(X,Y)&Cov(X,Z)\\[1.5ex]Cov(Y,X)&Var(Y)&Cov(Y,Z)\\[1.5ex]Cov(Z,X)&Cov(Z,Y)&Var(Z)\end{pmatrix}$

$\Sigma=\begin{pmatrix}7,6&11,2&-2,6\\[1.5ex]11,2&23,44&-4,36\\[1.5ex]-2,6&-4,36&3,44\end{pmatrix}$

သင်တွေ့မြင်ရသည့်အတိုင်း၊ matrix တစ်ခုတွင် ကွဲလွဲမှုများနှင့် ကွဲလွဲမှုများကို ကိုယ်စားပြုခြင်းဖြင့် variable များကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် အလွန်လွယ်ကူပါသည်။ အကြီးမားဆုံးကွဲလွဲမှုရှိသော ကိန်းရှင်သည် Y (23.44) ဖြစ်ပြီး အခြားတစ်ဖက်တွင် ကိန်းရှင် X နှင့် Y တို့သည် တိုက်ရိုက်ဆက်နွယ်မှုရှိပြီး ကိန်းရှင်များ X နှင့် Z (ထို့ကြောင့် Y နှင့် Z) တို့သည် ပြောင်းပြန်ဆက်နွယ်မှုရှိသည်။

ကိန်းရှင်နှစ်ခုကြားရှိ ကွဲလွဲချက်သည် ကိန်းရှင်များ၏ အစီအစဥ်ပေါ်တွင် မမူတည်သောကြောင့် ကာဗာရီယံမက်ထရစ်သည် အမြဲတမ်း အချိုးညီကြောင်း သတိပြုပါ။ ဥပမာအားဖြင့်,

$Cov(X,Y)$

ညီမျှသည်။

$Cov(Y,X).$

ထို့အပြင်၊ covariance matrix သည် အမြဲတမ်း square matrix ဖြစ်ပြီး ၎င်း၏အတိုင်းအတာသည် variable အရေအတွက်နှင့် ညီမျှမည်ဖြစ်သည်။ ဤအခြေအနေတွင် ကျွန်ုပ်တို့တွင် variable သုံးခုရှိသောကြောင့် ၎င်းသည် 3×3 matrix ဖြစ်သည်၊ သို့သော် ကျွန်ုပ်တို့တွင် variable နှစ်ခုသာရှိလျှင် coariance matrix သည် 2×2 ဖြစ်လိမ့်မည်။

ကွဲပြားမှု matrix ၏ ဂုဏ်သတ္တိများ

covariance matrix တွင် အောက်ပါလက္ခဏာများရှိသည်။

covariance matrix သည် variable အရေအတွက်၏ အစီအစဥ်၏ square matrix ဖြစ်သည်။
covariance matrix သည် symmetric ဖြစ်ပြီး ဆိုလိုသည်မှာ matrix ၏ အဓိကထောင့်ဖြတ်သည် symmetry ၏ ဝင်ရိုးတစ်ခုဖြစ်သည်။
covariance matrix သည် အမြဲတမ်း positive semi-definite ဖြစ်သည်။
ကွဲပြားမှုမက်ထရစ်၏ အဆုံးအဖြတ်သည် သုညနှင့် ညီမျှသည် သို့မဟုတ် ကြီးသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။