Spss တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုအား မည်သို့လုပ်ဆောင်ရမည်နည်း။

variable နှစ်ခုသည် linear ဆက်ဆံရေးတစ်ခုရှိသောအခါ၊ ၎င်းတို့၏ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန် ရိုးရှင်းသော linear regression ကို မကြာခဏအသုံးပြုနိုင်သည် ။

သို့သော်၊ ကိန်းရှင်နှစ်ခုသည် လိုင်းမဟုတ်သော ဆက်နွယ်မှုရှိနေသောအခါ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုသည် ကောင်းစွာအလုပ်မလုပ်နိုင်ပါ။ ဤအခြေအနေမျိုးတွင်၊ သင်သည် quadratic regression ကို သုံး၍ ကြိုးစားနိုင်သည်။

ဤသင်ခန်းစာသည် SPSS တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- SPSS ရှိ Quadratic Regression

အလုပ်လုပ်တဲ့နာရီအရေအတွက်နဲ့ ပျော်ရွှင်မှုကြားက ဆက်နွယ်မှုကို နားလည်ချင်တယ်ဆိုပါစို့။ ကျွန်ုပ်တို့တွင် တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်နှင့် ပတ်သက်သည့် အောက်ပါဒေတာနှင့် လူ 16 ဦးအတွက် ပျော်ရွှင်မှုအဆင့် (0 မှ 100 အထိ) အစီရင်ခံတင်ပြသည်-

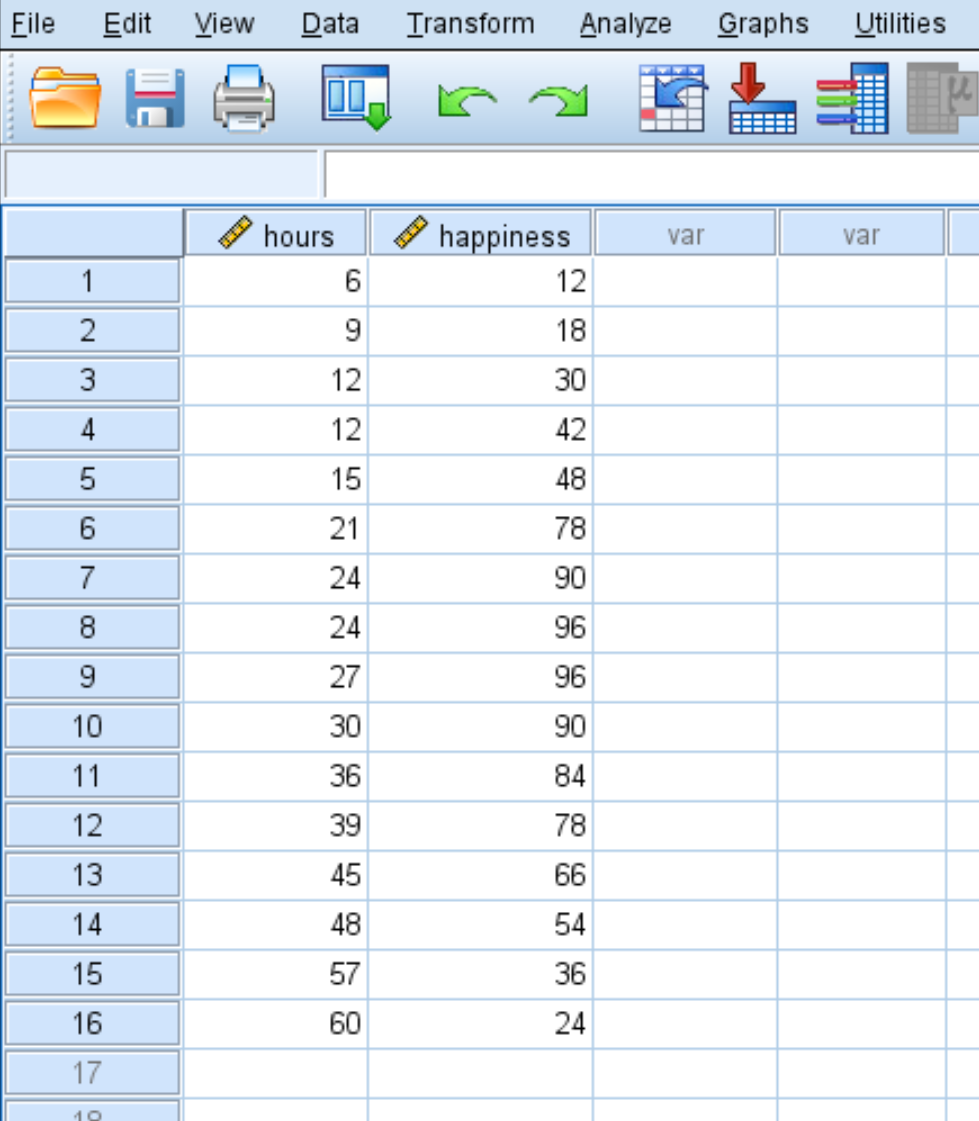
SPSS တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။

အဆင့် 1- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

quadratic regression ကိုမလုပ်ဆောင်မီ၊ ကိန်းရှင်နှစ်ခုသည် quadratic ဆက်နွယ်မှုရှိမရှိစစ်ဆေးရန် အလုပ်ချိန်နှင့် ပျော်ရွှင်မှုကြားဆက်ဆံရေးကို မြင်သာစေရန် အပိုင်းအစတစ်ခုကို ဖန်တီးကြပါစို့။

Charts tab ကိုနှိပ်ပါ၊ ထို့နောက် Chart Builder ကိုနှိပ်ပါ ။

ပေါ်လာသည့်ဝင်းဒိုးအသစ်တွင်၊ ရွေးချယ်ရန် စာရင်းမှ Scatter/Dot ကို ရွေးချယ်ပါ။ ထို့နောက် Simple Scatter ဟုအမည်တပ်ထားသောဇယားကို ပင်မတည်းဖြတ်ဝင်းဒိုးသို့ ဆွဲယူပါ။ ပြောင်းလဲနိုင်သော နာရီများကို x-ဝင်ရိုးပေါ်တွင် ဆွဲယူကာ y-ဝင်ရိုးပေါ်ရှိ ပျော်ရွှင်မှု ။ ထို့နောက် OK ကိုနှိပ်ပါ။

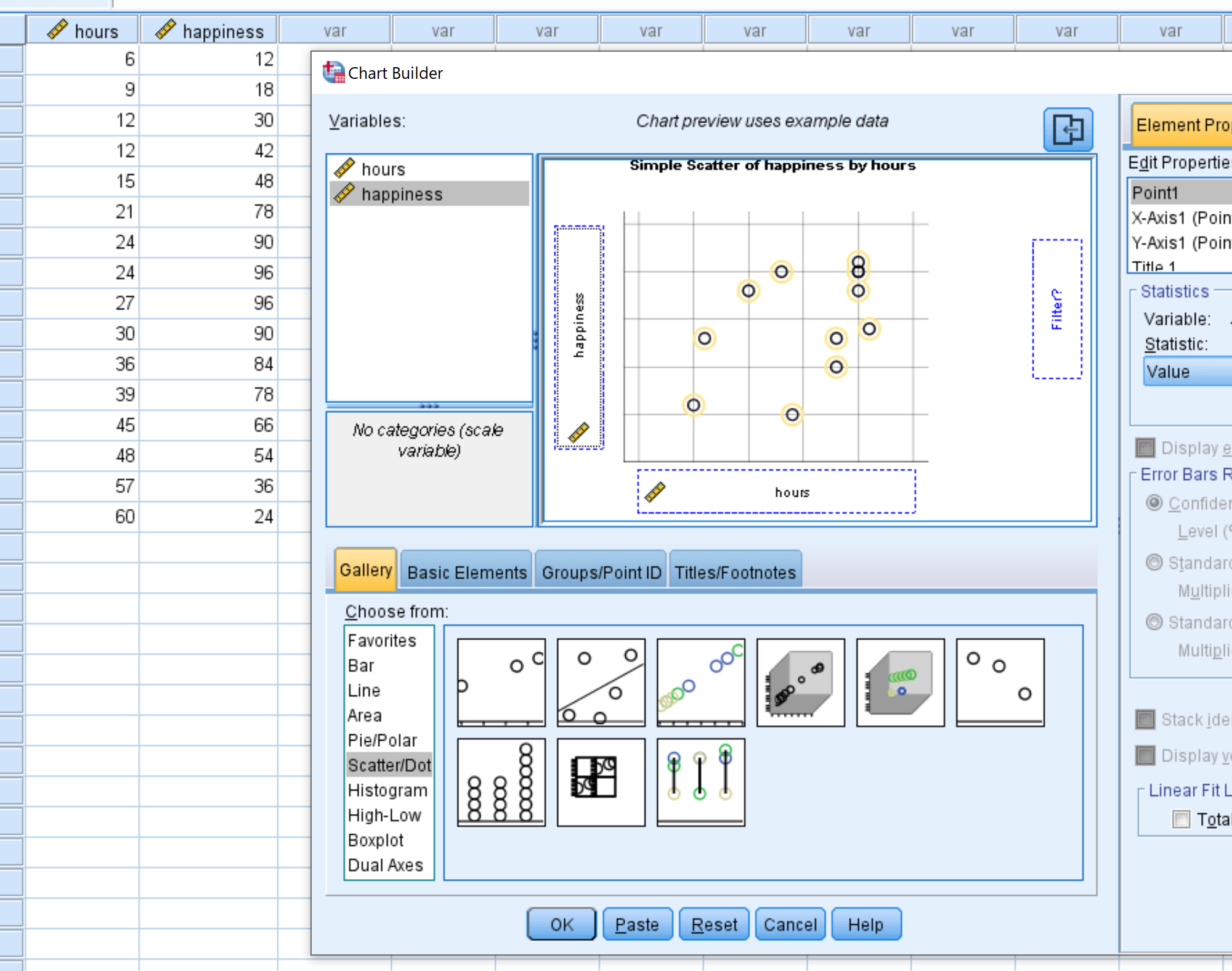
အောက်ဖော်ပြပါ ဖြန့်ကျက်ကွက်ပေါ်လာပါမည်-

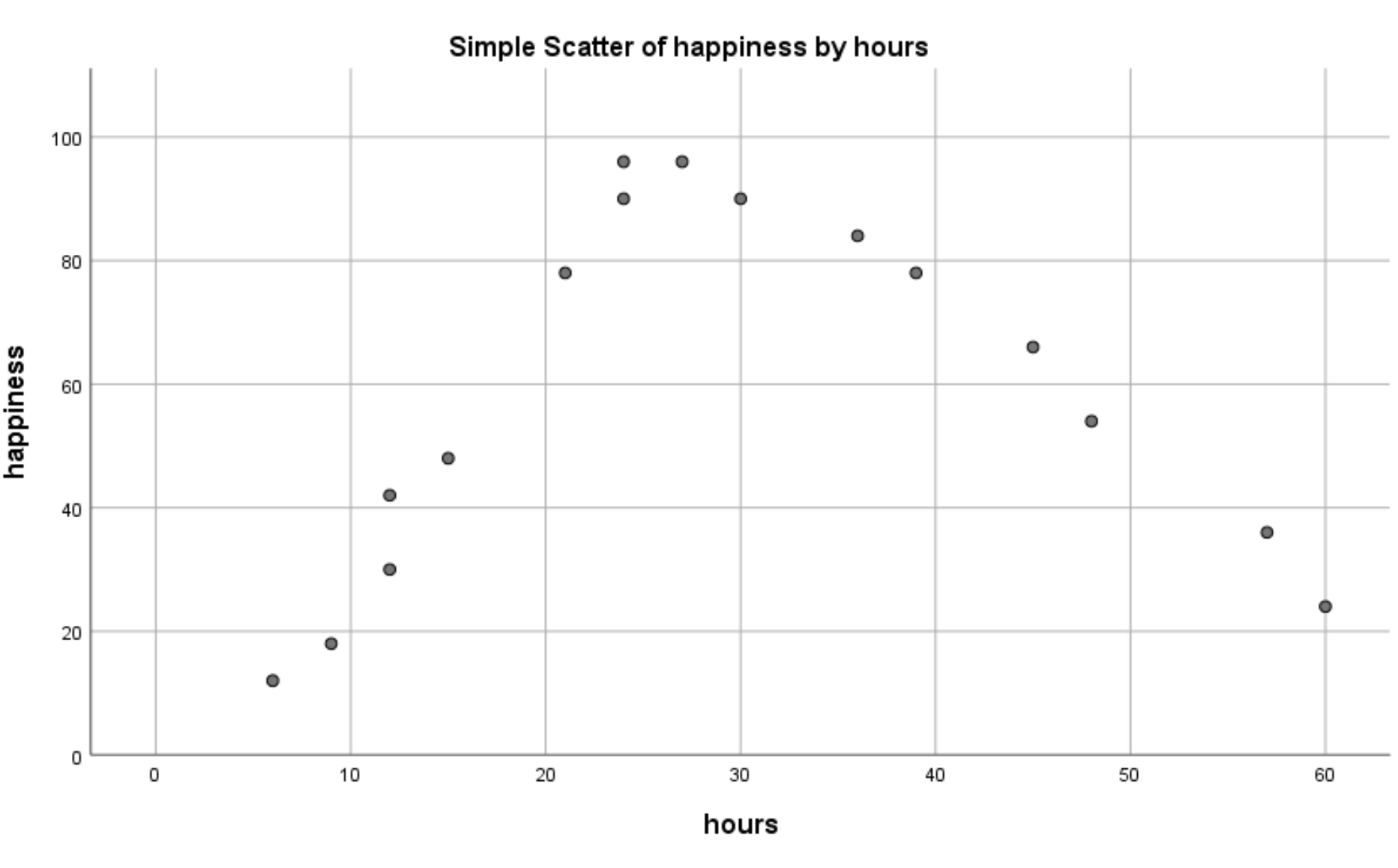
အလုပ်ချိန်နှင့် ပျော်ရွှင်မှုကြားတွင် တစ်ပြေးညီမဟုတ်သော ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့ ရှင်းရှင်းလင်းလင်း သိမြင်နိုင်ပါသည်။ ၎င်းသည် လေးပုံတပုံ ဆုတ်ယုတ်မှုအား ဤအခြေအနေတွင် အသုံးပြုရန် သင့်လျော်သော နည်းလမ်းတစ်ခုဖြစ်ကြောင်း ကျွန်ုပ်တို့အား ပြောပြသည်။

အဆင့် 2- ကိန်းရှင်အသစ်တစ်ခုကို ဖန်တီးပါ။

quadratic regression မလုပ်ဆောင်မီ၊ ကျွန်ုပ်တို့သည် နာရီ ² အတွက် ကြိုတင်ခန့်မှန်းကိန်းရှင်တစ်ခုကို ဖန်တီးရန် လိုအပ်ပါသည်။

Transformation tab ကိုနှိပ်ပါ၊ ထို့နောက် Calculate Variable ကိုနှိပ်ပါ ။

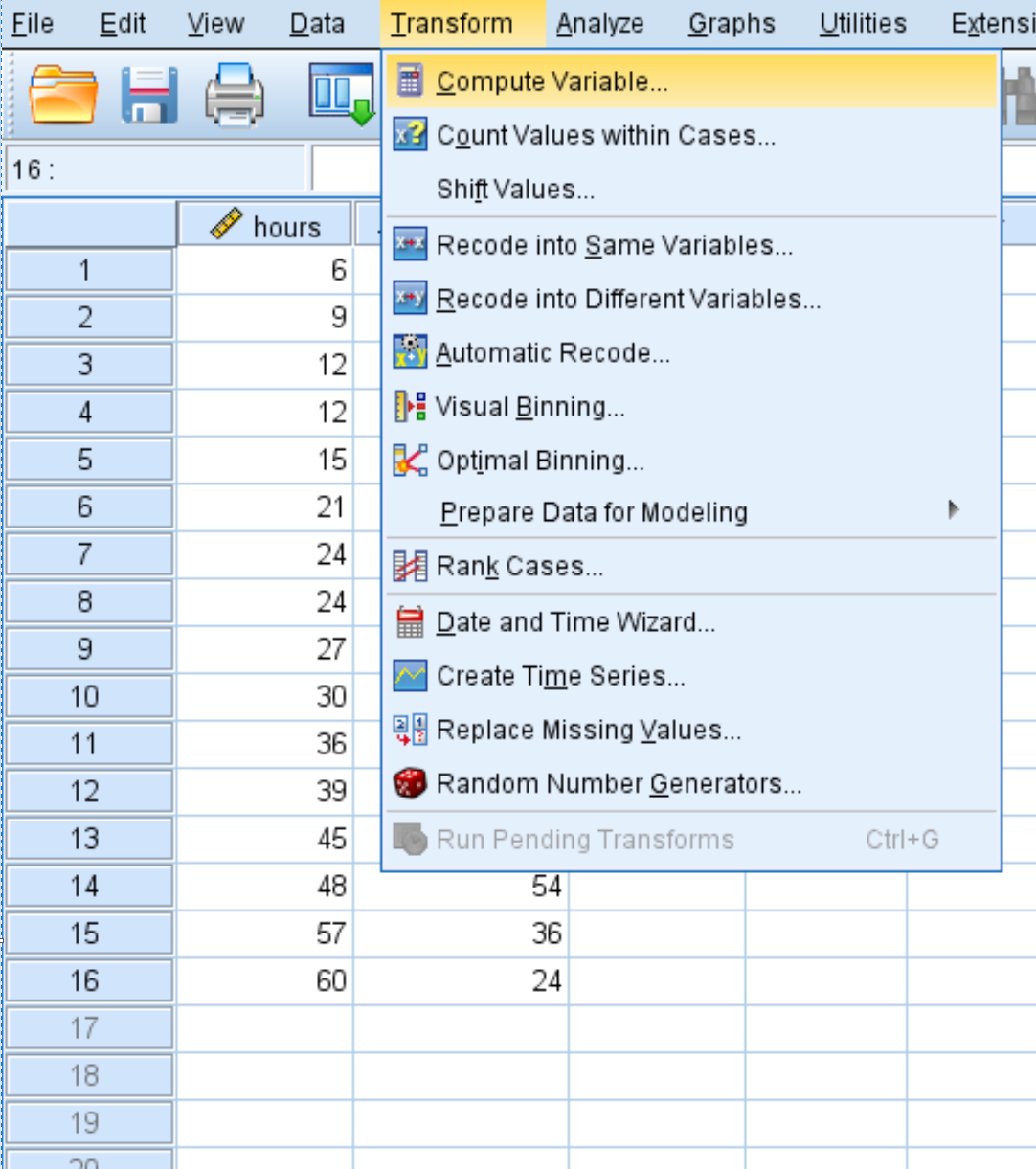
ပေါ်လာသည့်ဝင်းဒိုးအသစ်တွင်၊ ပစ်မှတ်ပြောင်းလဲနိုင်သော နာရီ 2 ကို အမည်ပေးပြီး နာရီ* နာရီ အဖြစ် သတ်မှတ်ပါ။

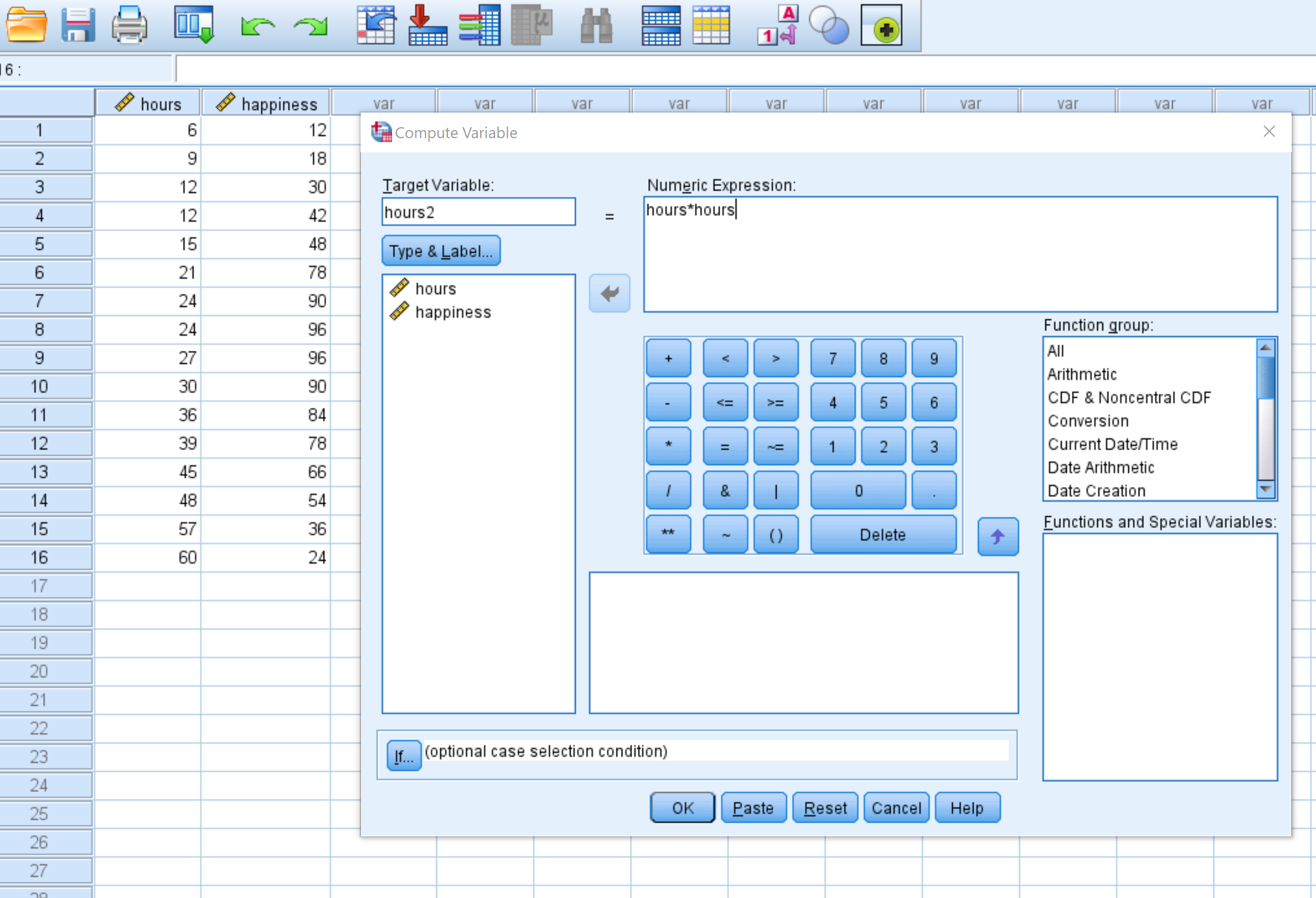
OK ကို နှိပ်လိုက်သည်နှင့် နာရီ 2 ကိန်းရှင်သည် ကော်လံအသစ်တစ်ခုတွင် ပေါ်လာလိမ့်မည်-

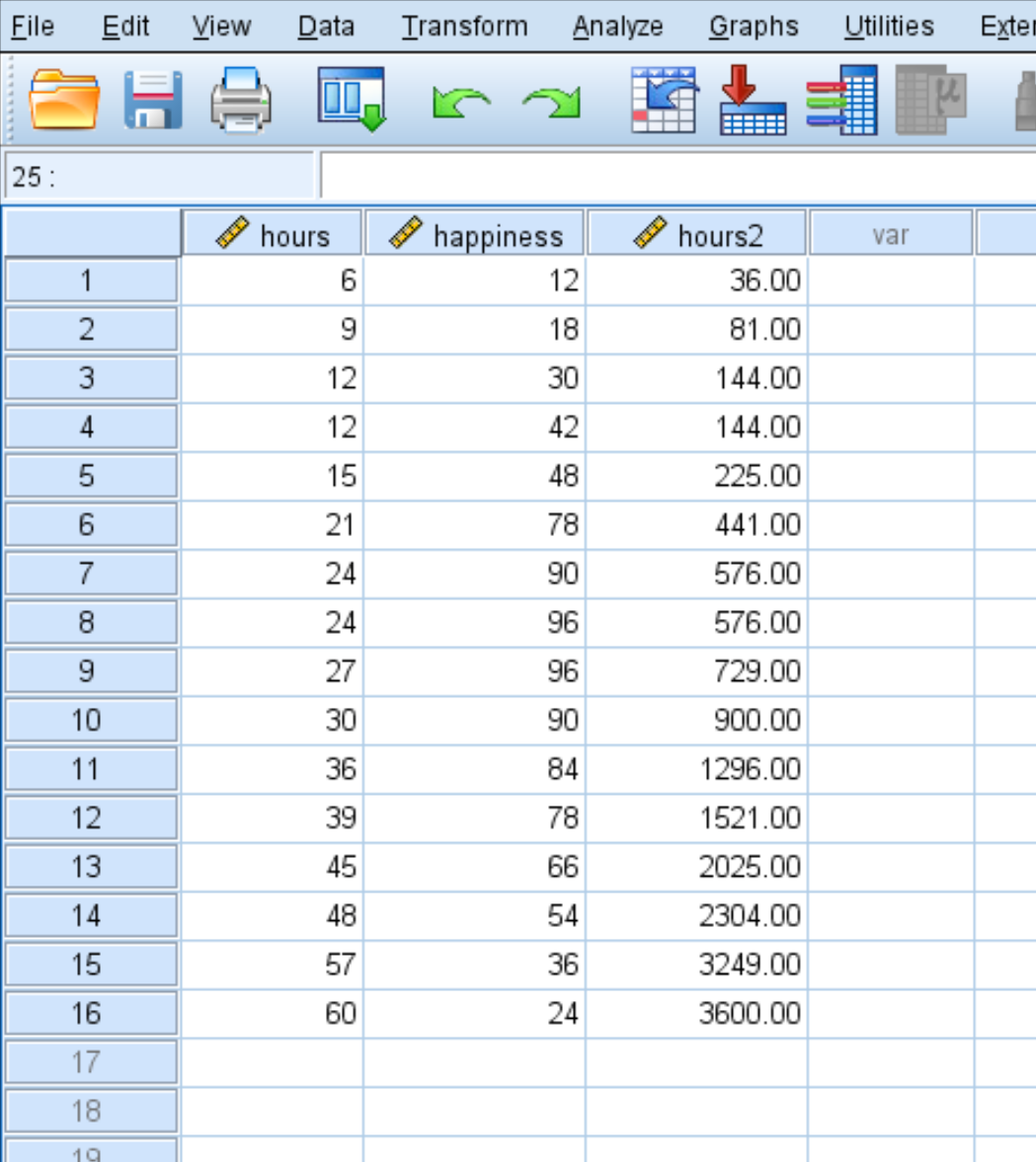
အဆင့် 3- လေးထောင့်ပုံစံ ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် လေးထောင့်ပုံသဏ္ဍန်ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါမည်။ Analyze tab ကိုနှိပ်ပါ၊ ထို့နောက် Regression ၊ ထို့နောက် Linear :

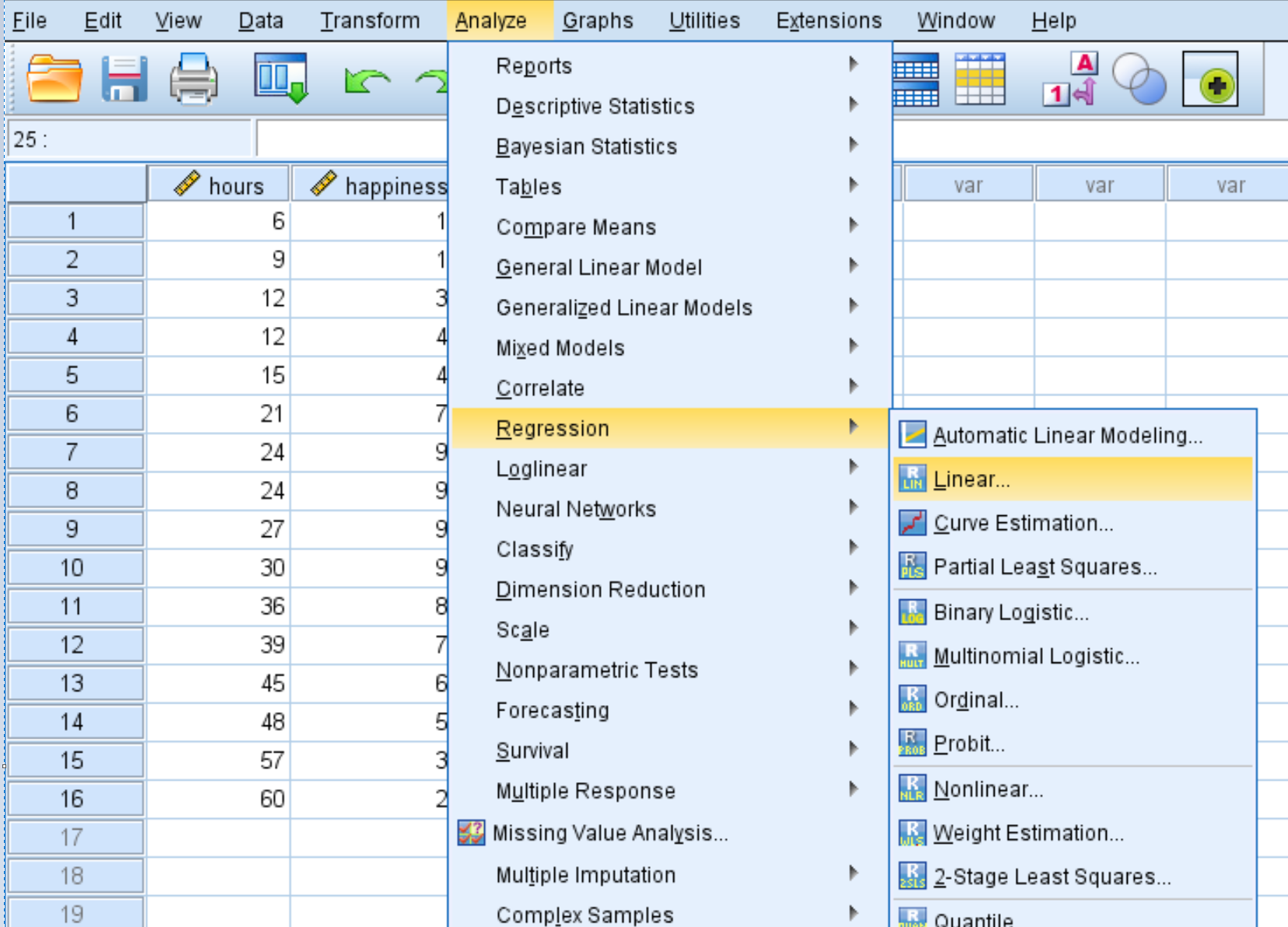
ပေါ်လာသည့် ဝင်းဒိုးအသစ်တွင်၊ မှီခိုမှုဟု အမည်တပ်ထားသည့် အကွက်ထဲသို့ ပျော်ရွှင်မှုကို ဆွဲယူပါ။ Independent(များ) ဟု အညွှန်းတပ်ထားသော အကွက်ထဲသို့ နာရီ နှင့် နာရီ 2 ကို ဆွဲထည့်ပါ။ ထို့နောက် OK ကိုနှိပ်ပါ။

အဆင့် 4: ရလဒ်များကို ဘာသာပြန်ပါ။

OK ကို နှိပ်လိုက်သည်နှင့်၊ လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှု ရလဒ်များသည် ဝင်းဒိုးအသစ်တွင် ပေါ်လာမည်ဖြစ်သည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော ပထမဇယားကို Model Summary ဟုခေါ်သည် ။

ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• R Square- ဤသည်မှာ ရှင်းလင်းချက် ကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ ပျော်ရွှင်မှုကွဲပြားမှု၏ 90.9% ကို နာရီ နှင့် နာရီ ² variable များဖြင့် ရှင်းပြနိုင်သည်။
• စံ။ ခန့်မှန်းချက်အမှား- စံအမှား သည် သတိပြုမိသောတန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြားရှိ ပျမ်းမျှအကွာအဝေးဖြစ်သည်။ ဤဥပမာတွင်၊ လေ့လာတွေ့ရှိထားသောတန်ဖိုးများသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ပျမ်းမျှယူနစ် 9,519 ဖြင့် သွေဖည်သွားပါသည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော နောက်ဇယားကို ANOVA ဟုခေါ်သည်။

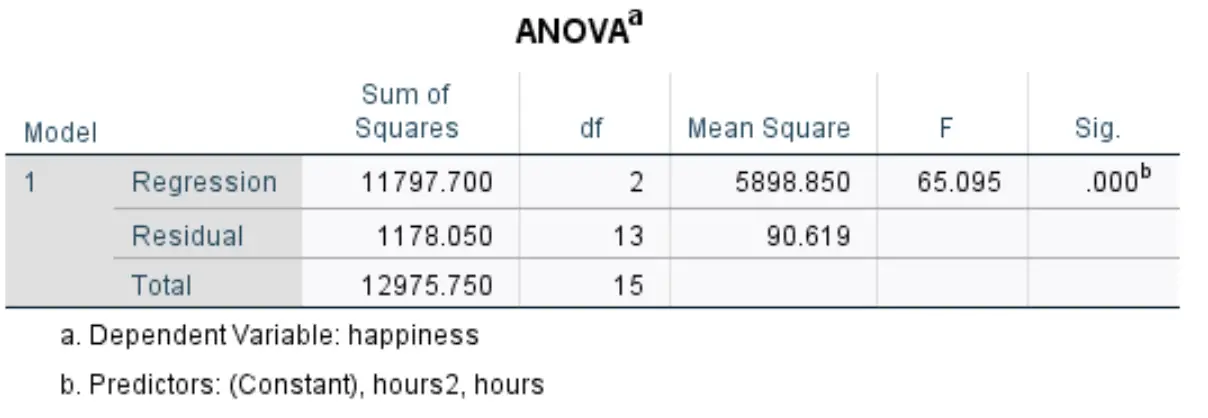
ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• F- ဤသည်မှာ Mean Square Regression / Mean Square Residual အဖြစ် တွက်ချက်ထားသော ဆုတ်ယုတ်မှုပုံစံအတွက် အလုံးစုံ F ကိန်းဂဏန်းဖြစ်သည်။
• Sig- ဤသည်မှာ အလုံးစုံ F ကိန်းဂဏန်းနှင့်ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။ ၎င်းသည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုလုံးအား ကိန်းဂဏန်းအချက်အလတ်အရ သိသာထင်ရှားမှုရှိ၊ မရှိ ကျွန်ုပ်တို့အား ပြောပြသည်။ ဤကိစ္စတွင်၊ p-value သည် 0.000 နှင့် ညီမျှပြီး၊ နာရီ နှင့် နာရီ ² ပေါင်းစပ်ထားသော ကိန်းရှင်များသည် စာမေးပွဲရလဒ်နှင့် စာရင်းအင်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိသည်ကို ညွှန်ပြပါသည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော အောက်ပါဇယားသည် Coefficients ခေါင်းစဉ်ဖြစ်သည်။

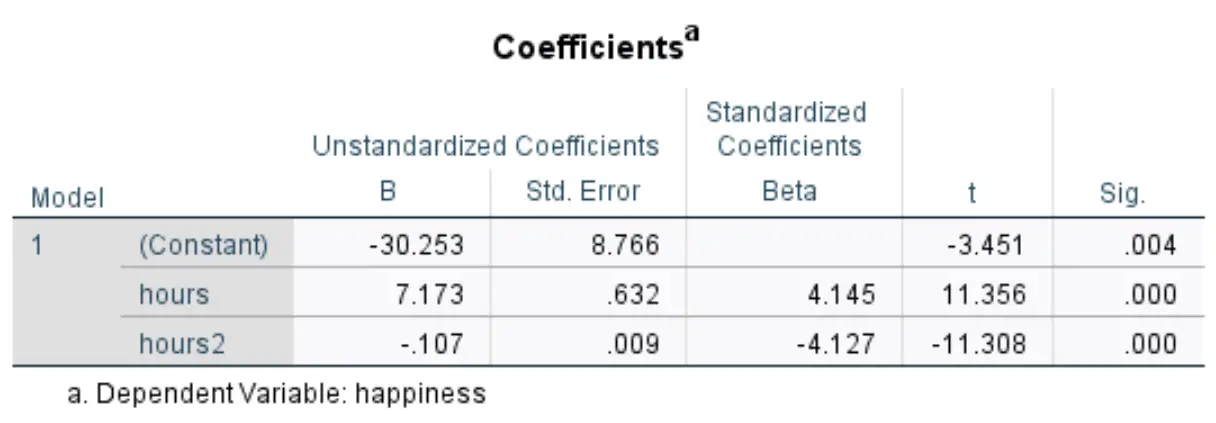
ဤဒေတာအတွဲအတွက် ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းကို ဖွဲ့စည်းရန် Standardized B ကော်လံရှိ တန်ဖိုးများကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

ခန့်မှန်းခြေ ပျော်ရွှင်မှုအဆင့် = -30.253 + 7.173*(နာရီ) – 0.107*(နာရီ ² )

တစ်ပတ်လျှင် အလုပ်လုပ်သည့် နာရီအရေအတွက်ပေါ်မူတည်၍ လူတစ်ဦးချင်းစီ၏ ခန့်မှန်းခြေ ပျော်ရွှင်မှုအဆင့်ကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။ ဥပမာအားဖြင့်၊ တစ်ပတ်လျှင် နာရီ 60 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 14.97 ရှိသင့်သည်-

ခန့်မှန်းပျော်ရွှင်မှုအဆင့် = -30.253 + 7.173*(60) – 0.107*(60 ² ) = 14.97 ။

အပြန်အလှန်အားဖြင့် တစ်ပတ်လျှင် နာရီ 30 အလုပ်လုပ်သူသည် ပျော်ရွှင်မှုအဆင့် 88.65 ရှိသင့်သည်-

ခန့်မှန်းပျော်ရွှင်မှုအဆင့် = -30.253 + 7.173*(30) – 0.107*(30 ² ) = 88.65 ။

အဆင့် 5: ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ လေးပုံတပုံ ဆုတ်ယုတ်မှု၏ ရလဒ်များကို အစီရင်ခံလိုပါသည်။ ဤသည်မှာ ဤအရာကို ပြုလုပ်ပုံ၏ ဥပမာတစ်ခုဖြစ်သည်။

လူတစ်ဦးချင်းစီမှ အလုပ်လုပ်သော နာရီအရေအတွက်နှင့် ၎င်းတို့၏ သက်ဆိုင်ရာ ပျော်ရွှင်မှုအဆင့် (0 မှ 100) အကြား ဆက်နွယ်မှုကို တွက်ချက်ရန် လေးလေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုတစ်ခုကို လုပ်ဆောင်ခဲ့သည်။ ခွဲခြမ်းစိတ်ဖြာမှုတွင် လူ ၁၆ ဦး၏ နမူနာကို အသုံးပြုခဲ့သည်။

ရလဒ်များသည် ရှင်းလင်းချက်ပြကွက်များ နာရီ နှင့် နာရီ ² နှင့် တုံ့ပြန်မှုပြောင်းလဲနိုင်သော ပျော်ရွှင်မှု (F(2, 13) = 65.095, p < 0.000) အကြား ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်ဆံရေးရှိကြောင်း ပြသခဲ့သည်။

ဤရှင်းပြချက်နှစ်ခုသည် ပျော်ရွှင်မှု၌ ကွဲပြားမှု၏ 90.9% ကို ပေါင်းစပ်ထားသည်။

ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

ခန့်မှန်းခြေ ပျော်ရွှင်မှုအဆင့် = -30.253 + 7.173 (နာရီ) – 0.107 ( ² နာရီ)