Bland-altman ဇာတ်ကွက်ဆိုတာ ဘာလဲ။ (အဓိပ္ပါယ် & #038; ဥပမာ)

Bland-Altman ဇာတ်ကွက်ကို မတူညီသော တူရိယာနှစ်ခု သို့မဟုတ် မတူညီသော တိုင်းတာမှုနည်းပညာနှစ်ခုကြားတွင် တိုင်းတာမှုကွာခြားချက်များကို မြင်သာစေရန် အသုံးပြုသည်။

၎င်းကို လက်ရှိအသုံးပြုနေသော တူရိယာ သို့မဟုတ် နည်းပညာတစ်ခုခုနှင့် တိုင်းတာခြင်းအတွက် တူရိယာအသစ် သို့မဟုတ် နည်းပညာ၏ ဆင်တူမှုများကို အကဲဖြတ်ရန် ၎င်းကို မကြာခဏ အသုံးပြုလေ့ရှိသည်။

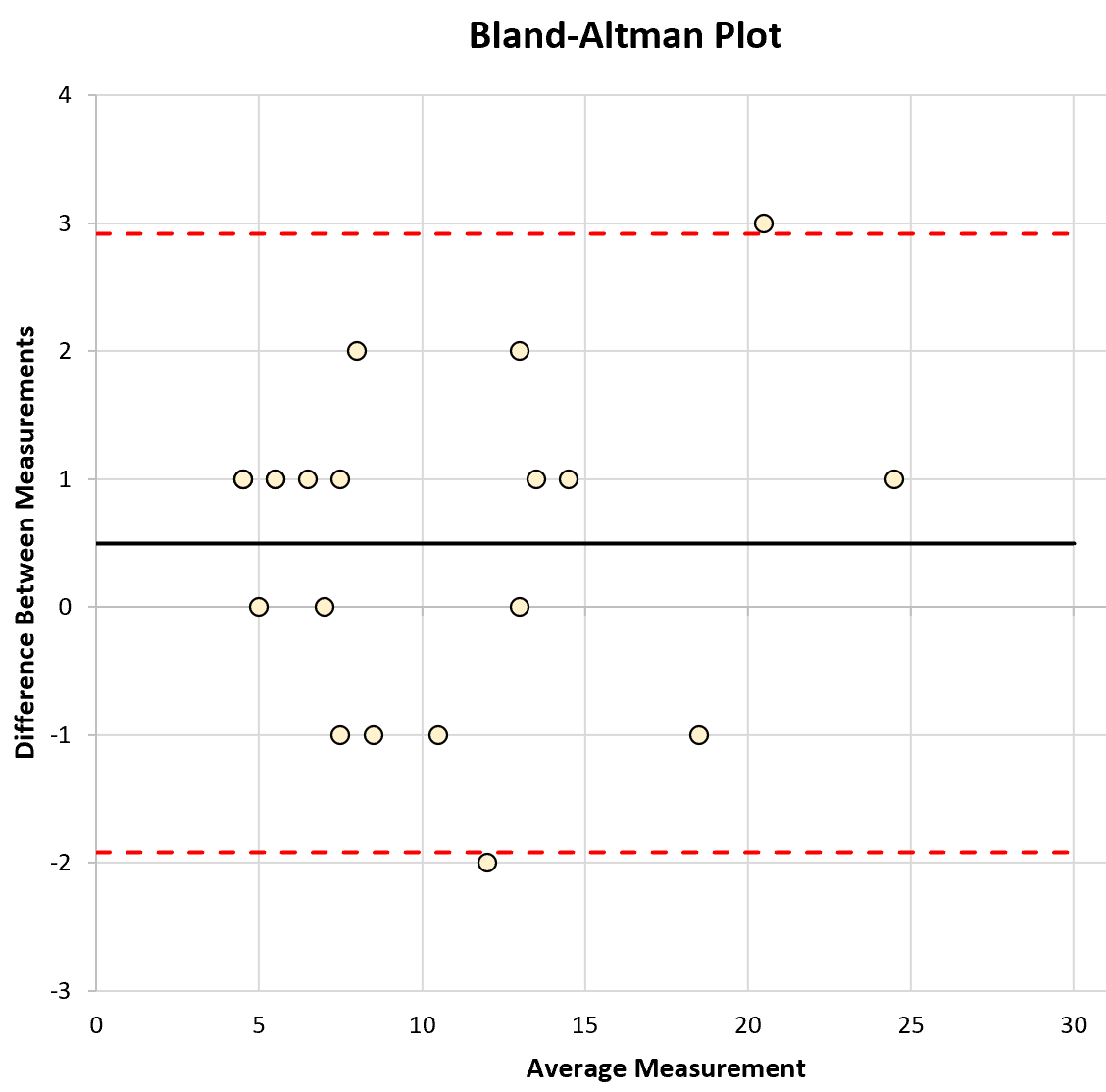
ကွက်၏ x-axis သည် တူရိယာနှစ်ခု၏ ပျမ်းမျှတိုင်းတာမှုကို ပြသပြီး y-axis သည် တူရိယာနှစ်ခုကြားရှိ တိုင်းတာမှုကွာခြားချက်ကို ပြသသည်။

အောက်ဖော်ပြပါ စာကြောင်းသုံးကြောင်းကိုလည်း ဇာတ်ကွက်တွင် ဖော်ပြထားသည်။

• တူရိယာနှစ်ခုကြား တိုင်းတာမှု ပျမ်းမျှကွာခြားချက်
• ပျမ်းမျှခြားနားမှုအတွက် 95% ယုံကြည်မှုကြားကာလ၏ အထက်ကန့်သတ်ချက်
• ပျမ်းမျှခြားနားမှုအတွက် 95% ယုံကြည်မှုကြားကာလ၏ အနိမ့်ဆုံးကန့်သတ်ချက်

ဤဇာတ်ကွက်အမျိုးအစားသည် အရာနှစ်ခုကို ဆုံးဖြတ်ရန်အတွက် အသုံးဝင်သည်-

1. တူရိယာနှစ်ခုကြား တိုင်းတာမှု ပျမ်းမျှကွာခြားချက်ကဘာလဲ။

ဂရပ်အလယ်တွင် ရေးဆွဲထားသော အလျားလိုက်မျဉ်းသည် တူရိယာနှစ်ခုကြားရှိ တိုင်းတာမှုဆိုင်ရာ ပျမ်းမျှကွာခြားချက်ကို ပြသသည်။ ဤတန်ဖိုးကို တူရိယာများအကြား “ဘက်လိုက်မှု” ဟု မကြာခဏ ရည်ညွှန်းသည်။

နောက်ထပ် ဤတန်ဖိုးသည် သုညမှဖြစ်ပြီး၊ တူရိယာများကြား တိုင်းတာမှု ပျမ်းမျှကွာခြားချက် ပိုများလေဖြစ်သည်။

2. တူရိယာနှစ်ခုကြား သဘောတူညီချက်၏ ပုံမှန်အတိုင်းအတာသည် အဘယ်နည်း။

အပေါ်နှင့်အောက် ယုံကြည်မှုကြားကာလမျဥ်းများသည် တူရိယာနှစ်ခုကြားရှိ ပုံမှန်သဘောတူညီချက်၏ အယူအဆတစ်ခုကို ပေးသည်။ ယေဘူယျအားဖြင့်၊ တူရိယာနှစ်ခုကြားရှိ ကွာခြားချက်များ၏ 95% သည် ဤယုံကြည်မှုကန့်သတ်ချက်များအတွင်း ကျရောက်နေသည်။

ယုံကြည်မှုကြားကာလ ပိုကျယ်လေ၊ တူရိယာနှစ်ခုကြားရှိ တိုင်းတာမှုကွာဟချက် ကျယ်ပြန့်လေဖြစ်သည်။

အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် Bland-Altman ဇာတ်ကွက်ကို အစမှနေ၍ မည်သို့ဖန်တီးပြီး အဓိပ္ပာယ်ဖွင့်ရမည်ကို ပြသထားသည်။

မှတ်ချက်- Bland-Altman ဇာတ်ကွက်ကို တစ်ခါတစ်ရံ Tukey ဆိုလိုသည့် ကွဲပြားမှုဇာတ်ကွက်ဟု ခေါ်သည်။ ဤအမည်များကို အပြန်အလှန်အသုံးပြုကြသည်။

အဆင့် 1: ဒေတာစုဆောင်းပါ။

ဇီဝဗေဒပညာရှင်တစ်ဦးသည် ဖားများ၏အလေးချိန်ကို ဂရမ်ဖြင့်တိုင်းတာရန်အတွက် ဆင်တူသည့်တူရိယာနှစ်မျိုးကို သိချင်သည်ဆိုပါစို့။ သူသည် တူညီသောဖား 20 ကိုအလေးချိန်ထိန်းရန် တူရိယာနှစ်ခု (A နှင့် B) ကိုအသုံးပြုသည်။

တူရိယာတစ်ခုစီဖြင့် တိုင်းတာထားသော ဖားများ၏အလေးချိန်ကို အောက်ပါဇယားတွင် ပြထားသည်။

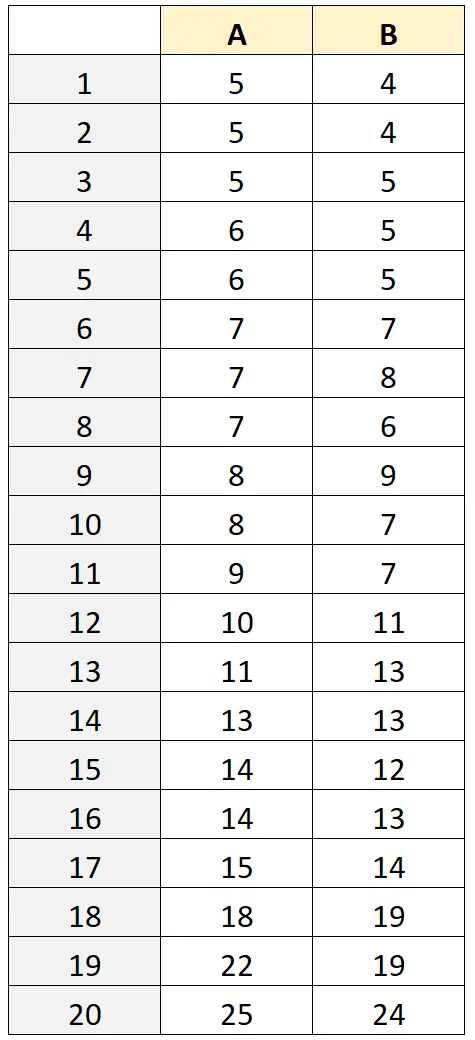
အဆင့် 2- ပျမ်းမျှတိုင်းတာမှုနှင့် တိုင်းတာမှုကွာခြားချက်ကို တွက်ချက်ပါ။

ထို့နောက်၊ ဖားတစ်ခုစီအတွက် ပျမ်းမျှအတိုင်းအတာ ((A+B)/2) နှင့် တိုင်းတာမှုကွာခြားချက် (AB) ကို တွက်ချက်ပါမည်။

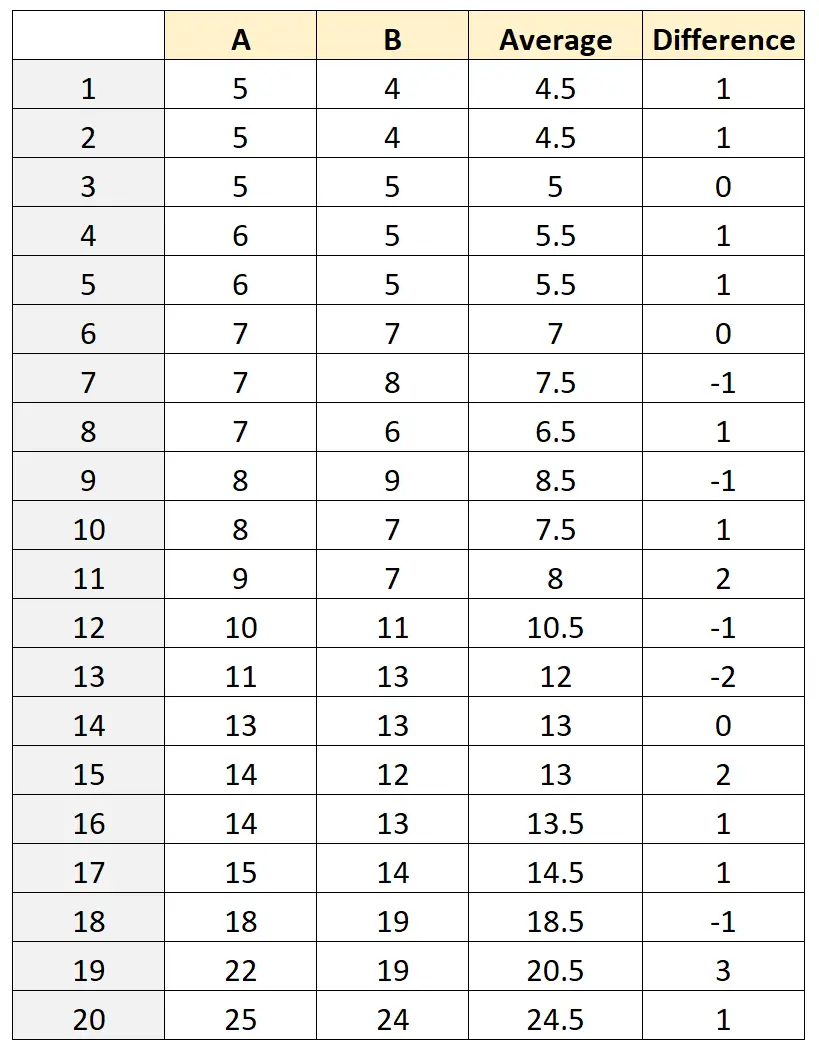
အဆင့် 3- ပျမ်းမျှကွာခြားချက်နှင့် ယုံကြည်မှုကြားကာလကို တွက်ချက်ပါ။

Difference ကော်လံရှိ တန်ဖိုးများ၏ ပျမ်းမျှသည် 0.5 ဖြစ်သွားသည်။

Difference ကော်လံရှိ တန်ဖိုးများ၏ စံသွေဖည်မှုသည် 1.235 ဖြစ်သွားသည်။

ပျမ်းမျှခြားနားမှုအတွက် ယုံကြည်မှုကြားကာလ၏ အထက်နှင့်အောက် ကန့်သတ်ချက်များကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်-

အထက်ကန့်သတ်ချက်- x + 1.96*s = 0.5 + 1.96*1.235 = 2.92

အနိမ့်ဆုံးကန့်သတ်ချက်- x – 1.96*s = 0.5 – 1.96*1.235 = -1.92

ဤတန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံမှာ အောက်ပါအတိုင်းဖြစ်သည်။

• ပျမ်းမျှအားဖြင့် တူရိယာ A သည် တူရိယာ B ထက် ၀.၅ ဂရမ် ပိုအလေးချိန်ရှိသည်။
• တူရိယာနှစ်ခုကြားရှိ အလေးချိန်ကွာခြားချက်၏ 95% သည် -1.92 ဂရမ်နှင့် 2.92 ဂရမ်ကြားဖြစ်သင့်သည်။

ထို့နောက် ဤတန်ဖိုးများကို မြင်ယောင်နိုင်ရန် Bland-Altman ဇာတ်ကွက်ကို ဖန်တီးပါမည်။

အဆင့် 4: Plot ကိုဖန်တီးပါ။

ထို့နောက် x-axis ပေါ်ရှိ တူရိယာနှစ်ခု၏ ပျမ်းမျှတိုင်းတာမှုနှင့် y ဝင်ရိုးပေါ်ရှိ တိုင်းတာမှုအကြား ကွာခြားချက်ကို ပြသသည့် အောက်ပါကွက်ကွက်ကို ဖန်တီးနိုင်သည်။

တိုင်းတာချက်များ (0.5) နှင့် အထက်ယုံကြည်မှုကန့်သတ်ချက် (2.92) နှင့် ယခင်အဆင့်တွင် တွက်ချက်ထားသည့် ယုံကြည်စိတ်ချရမှု ကန့်သတ်ချက် (-1.92) တို့အကြား အလျားလိုက်မျဉ်းကြောင်းကိုလည်း ထည့်နိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

Excel တွင် Bland-Altman Plot ကိုဖန်တီးနည်း
R တွင် Bland-Altman ဇာတ်ကွက်ဖန်တီးနည်း
Python တွင် Bland-Altman Plot ကိုဖန်တီးနည်း