မညီမျှသောနမူနာအရွယ်အစားများဖြင့် anova ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

စာရင်းအင်းနှင့်ပတ်သက်လာလျှင် ကျောင်းသားများ မကြာခဏမေးလေ့ရှိသောမေးခွန်းမှာ-

အုပ်စုတစ်ခုစီ၏နမူနာအရွယ်အစားများ မညီသောအခါ တစ်လမ်းသွား ANOVA လုပ်ဆောင်ရန် ဖြစ်နိုင်ပါသလား။

အတိုကောက် အဖြေ-

ဟုတ်ပါသည်၊ နမူနာအရွယ်အစားများ မညီသောအခါ တစ်ကြောင်း ANOVA လုပ်ဆောင်နိုင်သည်။ တူညီသောနမူနာအရွယ်အစားများသည် ANOVA တွင်ပြုလုပ်ထားသည့် ယူဆချက်တစ်ခုမဟုတ် ပါ။

သို့သော်၊ မညီမျှသောနမူနာအရွယ်အစားများဖြင့် တစ်လမ်းသွား ANOVA ကိုလုပ်ဆောင်ရာတွင် ထည့်သွင်းစဉ်းစားရမည့် အလားအလာပြဿနာနှစ်ခုရှိသည်။

(၁) စာရင်းအင်းဆိုင်ရာ စွမ်းအားကို လျှော့ချပါ။

(၂) ကြံ့ခိုင်မှုအား မညီမျှသောကွဲလွဲမှုသို့ လျော့ကျစေပါသည်။

အောက်ဖော်ပြပါကဏ္ဍများသည် ဤဖြစ်နိုင်ချေပြဿနာနှစ်ခုကို အသေးစိတ်ရှင်းပြထားသည်။

ပြဿနာ # 1- စာရင်းအင်းဆိုင်ရာ ပါဝါကို လျှော့ချထားသည်။

အုပ်စုများကို နှိုင်းယှဉ်ရန် ကိန်းဂဏန်းစမ်းသပ်မှု အမျိုးအစားကို အသုံးပြုသောအခါ၊ အုပ်စုတစ်ခုစီသည် တူညီသောနမူနာအရွယ်အစားရှိသောအခါ စစ်ဆေးမှု၏ ကိန်းဂဏန်းစွမ်းအားသည် အမြင့်ဆုံးဖြစ်သည်။

ကိန်းဂဏန်းဆိုင်ရာ ပါဝါသည် အမှန်တကယ်ရှိသည့်အခါ စမ်းသပ်မှုတစ်ခုမှ အကျိုးသက်ရောက်မှုကို ထောက်လှမ်းနိုင်သည့် ဖြစ်နိုင်ခြေကို ရည်ညွှန်းကြောင်း သတိရပါ။

အုပ်စုများကြားနမူနာအရွယ်အစား ကွာခြားချက်များ ပိုများလေ၊ ANOVA ၏ ကိန်းဂဏန်းဆိုင်ရာ ပါဝါ နည်းပါးလေဖြစ်ကြောင်း ပြသနိုင်သည်။

ထို့ကြောင့် သုတေသီများသည် ယေဘူယျအားဖြင့် စွမ်းအားပိုမြင့်စေရန်အတွက် တူညီသောနမူနာအရွယ်အစားများကို လိုချင်ကြပြီး ထို့ကြောင့် စစ်မှန်သောကွဲပြားမှုများကို ရှာဖွေတွေ့ရှိနိုင်ခြေ ပိုများသည်။

မညီမျှသောနမူနာအရွယ်အစားများဖြင့် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်ရန် သေချာပေါက်ဖြစ်နိုင်သော်လည်း တစ်လမ်းသွား ANOVA ၏ ပါဝါ လျော့နည်းသွားမည်ကို သတိပြုသင့်သည်။

ပြဿနာ # 2- ကြံ့ခိုင်မှု မညီမျှခြင်းသို့ လျော့ကျသွားသည်။

တစ်လမ်းသွား ANOVA ၏ ယူဆချက်တစ်ခုမှာ အုပ်စုတစ်ခုစီကြား ကွဲလွဲမှုမှာ ညီမျှသည်။

ယေဘူယျအားဖြင့်၊ တစ်လမ်းသွား ANOVA သည် တူညီသောကွဲလွဲမှုယူဆချက်အား ချိုးဖောက်ခြင်းအတွက် ခိုင်ခံ့သည်ဟု ယူဆ သော်လည်း အုပ်စုတစ်ခုစီတွင် တူညီသောနမူနာအရွယ်အစားရှိမှသာလျှင် ။

ထို့ကြောင့်၊ သင့်တွင် မညီမျှသောနမူနာအရွယ်အစားများနှင့် အုပ်စုများကြား မညီမျှသောကွဲလွဲမှုများရှိပါက၊ တစ်လမ်းတည်း ANOVA ၏ရလဒ်များကို ယုံကြည်ရန်ခက်ခဲပေမည်။

မညီမျှသောနမူနာအရွယ်အစားများဖြင့် တစ်လမ်းသွား ANOVA ကို အသုံးပြုရန် ဆုံးဖြတ်နည်း

သင့်တွင် မညီမျှသောနမူနာအရွယ်အစားများရှိပြီး အုပ်စုနည်းလမ်းများကြား ကွဲပြားမှုများကို စမ်းသပ်ရန်အတွက် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်လိုပါက၊ မည်သို့ဆက်လက်လုပ်ဆောင်ရမည်ကို ဆုံးဖြတ်ရန် အောက်ပါ flowchart ကို အသုံးပြုနိုင်ပါသည်။

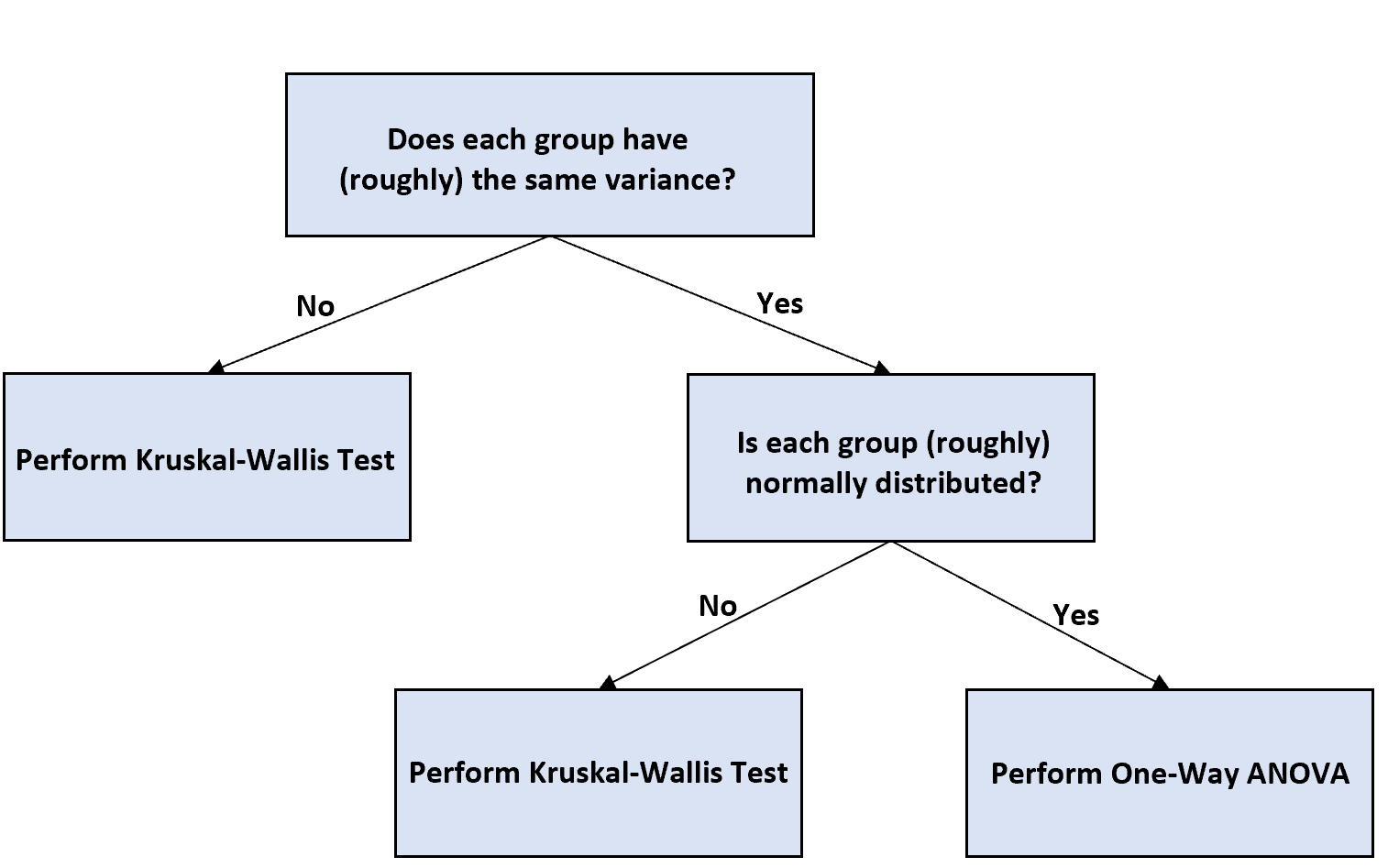
ဤသည်မှာ flowchart ၏ အကျဉ်းချုပ် ရှင်းလင်းချက်ဖြစ်သည် ။

အဆင့် 1- အုပ်စုတစ်ခုစီတွင် တူညီသောကွဲလွဲမှုရှိမရှိ ဆုံးဖြတ်ပါ။

အုပ်စုတစ်ခုစီတွင် ကွဲပြားမှုရှိမရှိ ဆုံးဖြတ်ရန်၊ ချဉ်းကပ်မှု နှစ်ခုထဲမှ တစ်ခုကို အသုံးပြုနိုင်သည်။

• အုပ်စုတစ်ခုစီအတွက် ကွက်လပ်များကို ဖန်တီးပြီး အုပ်စုတစ်ခုစီရှိ တန်ဖိုးများ ဖြန့်ဝေမှုမှာ ခန့်မှန်းခြေအားဖြင့် တူညီမှုရှိမရှိ ကြည့်ရှုပါ။
• Bartlett’s test ကဲ့သို့ တူညီသောကွဲပြားမှုများအတွက် တရားဝင်ကိန်းဂဏန်းစမ်းသပ်မှုပြုလုပ်ပါ။

ကွဲလွဲမှုများ မညီပါက၊ တစ်လမ်းမောင်း ANOVA နှင့် ညီမျှသော စံနှုန်းမဟုတ်သော စံနှုန်းမဟုတ်ဟု ယူဆသည့် Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်ပါ။

ကွာဟချက်များ ညီမျှပါက နောက်တစ်ဆင့်သို့ ဆက်သွားပါ။

အဆင့် 2- အုပ်စုတစ်ခုစီကို ပုံမှန်ဖြန့်ဝေခြင်းရှိမရှိ ဆုံးဖြတ်ပါ။

အုပ်စုတစ်ခုစီရှိ တန်ဖိုးများကို ခန့်မှန်းခြေအားဖြင့် ပုံမှန်ဖြန့်ဝေခြင်း ရှိ၊ မရှိ ဆုံးဖြတ်ရန်၊ ချဉ်းကပ်မှု နှစ်ခုထဲမှ တစ်ခုကို သင်သုံးနိုင်သည်-

• အုပ်စုတစ်ခုစီအတွက် ဟစ်စတိုဂရမ်များ သို့မဟုတ် QQ ကွက်များကို ဖန်တီးပါ။
• Shapiro-Wilk၊ Kolmogorov-Smironov၊ Jarque-Barre၊ သို့မဟုတ် D’Agostino-Pearson ကဲ့သို့သော တရားဝင်စာရင်းအင်းစစ်ဆေးမှုများကို ပြုလုပ်ပါ။

အုပ်စုတစ်ခုစီကို ပုံမှန်ဖြန့်ဝေပါက၊ သင်သည် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်နိုင်ပြီး ရလဒ်များကို သာမန်တစ်လမ်းသွား ANOVA ကဲ့သို့ အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်ပါသည်။

အုပ်စုတစ်ခုစီကို ပုံမှန်ဖြန့်ဝေခြင်းမရှိပါက၊ ၎င်းအစား Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

One-Way ANOVA မိတ်ဆက်
ANOVA ယူဆချက်များကို စစ်ဆေးနည်း
Kruskal-Wallis စမ်းသပ်မှုမိတ်ဆက်
ANOVA တွင် F တန်ဖိုးနှင့် P တန်ဖိုးကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုမည်နည်း။