Anova နှင့် ဆုတ်ယုတ်မှု- ကွာခြားချက်ကား အဘယ်နည်း။

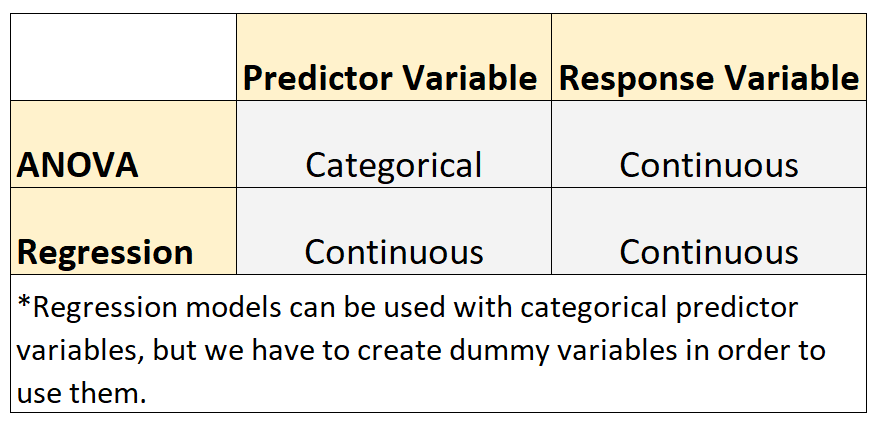
စာရင်းဇယားများတွင် အသုံးများသော မော်ဒယ်နှစ်ခုမှာ ANOVA နှင့် regression မော်ဒယ်များဖြစ်သည်။

ဤမော်ဒယ်နှစ်မျိုးသည် အောက်ဖော်ပြပါ တူညီမှုကို မျှဝေပါသည်။

• မော်ဒယ်တစ်ခုစီရှိ တုံ့ပြန်မှုကိန်းရှင် သည် ဆက်တိုက်ဖြစ်သည်။ စဉ်ဆက်မပြတ် ပြောင်းလဲနိုင်သော ဥပမာများတွင် အလေးချိန်၊ အရပ်၊ အလျား၊ အနံ၊ အချိန်၊ အသက်၊ အစရှိသည်တို့ ပါဝင်သည်။

သို့သော်၊ ဤမော်ဒယ်နှစ်မျိုးသည် အောက်ပါ ကွာခြားချက်ကို မျှဝေပါသည်။

• ကြိုတင်ခန့်မှန်းကိန်းရှင်များသည် အမျိုးအစားခွဲခြားသည့်အခါ ANOVA မော်ဒယ်များကို အသုံးပြုသည်။ အမျိုးအစားခွဲခြားနိုင်သော ကိန်းရှင်နမူနာများတွင် ပညာရေးအဆင့်၊ မျက်လုံးအရောင်၊ အိမ်ထောင်ရေးအခြေအနေ၊ စသည်တို့ပါဝင်သည်။
• ကြိုတင်ခန့်မှန်းကိန်းရှင်များ ဆက်တိုက်ဖြစ်နေသောအခါ ဆုတ်ယုတ်မှုပုံစံများကို အသုံးပြုပါသည်။*

* Regression မော်ဒယ်များကို categorical ကြိုတင်ခန့်မှန်းနိုင်သော ကိန်းရှင်များနှင့်အတူ သုံးနိုင်သော်လည်း ၎င်းတို့ကို အသုံးပြုရန်အတွက် dummy variable များကို ဖန်တီးရန် လိုအပ်ပါသည်။

အောက်ပါဥပမာများသည် ANOVA သို့မဟုတ် ဆုတ်ယုတ်မှုပုံစံများကို လက်တွေ့တွင် မည်သည့်အချိန်တွင် အသုံးပြုရမည်နည်း။

ဥပမာ 1- ဦးစားပေး ANOVA မော်ဒယ်

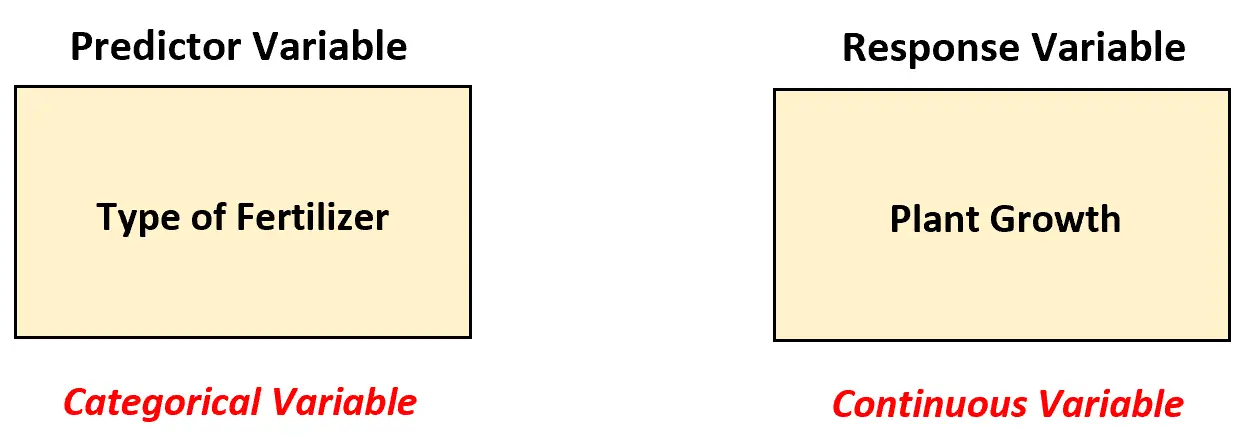
ဇီဝဗေဒပညာရှင်တစ်ဦးသည် တစ်လတာကာလအတွင်း တူညီသော ပျမ်းမျှအပင်ကြီးထွားမှု (လက်မအတွင်း) ကွဲပြားသော ဓာတ်မြေသြဇာ လေးမျိုးအား ဖြစ်ပေါ်စေခြင်း ရှိ၊ မရှိ နားလည်လိုသည်ဆိုပါစို့။ ၎င်းကိုစမ်းသပ်ရန်အတွက် သူမသည် အပင် 20 တွင် ဓာတ်မြေသြဇာတစ်ခုစီကို အသုံးပြုပြီး တစ်လအကြာတွင် အပင်တစ်ပင်ချင်းစီ၏ကြီးထွားမှုကို မှတ်တမ်းတင်သည်။

ဤအခြေအနေတွင်၊ ဇီဝဗေဒပညာရှင်သည် မြေသြဇာများအကြား ကွဲပြားမှုများကို ခွဲခြမ်းစိတ်ဖြာရန် တစ်လမ်းသွား ANOVA မော်ဒယ်ကို အသုံးပြုရမည်ဖြစ်ပြီး ကြိုတင်ခန့်မှန်းနိုင်သော ကိန်းရှင်နှင့် ၎င်းသည် အမျိုးအစားအလိုက် ရှိနေသောကြောင့် ဖြစ်သည်။

တစ်နည်းဆိုရသော်၊ ခန့်မှန်းသူ variable ၏တန်ဖိုးများကို အောက်ပါ “ အမျိုးအစားများ” တွင် ခွဲခြားနိုင်ပါသည်။

• မြေသြဇာ ၁
• မြေသြဇာ ၂
• မြေသြဇာ ၃
• ဓာတ်မြေသြဇာ ၄

တစ်လမ်းသွား ANOVA သည် ဇီဝဗေဒပညာရှင်အား မတူညီသော ဓာတ်မြေသြဇာလေးမျိုးကြားတွင် ပျမ်းမျှအပင်ကြီးထွားမှုနှင့် ညီမျှသည်ရှိမရှိ ဇီဝဗေဒပညာရှင်အား ပြောပြလိမ့်မည်။

ဥပမာ 2- နှစ်သက်သော ဆုတ်ယုတ်မှုပုံစံ

အိမ်ခြံမြေအကျိုးဆောင်တစ်ဦးသည် စတုရန်းပေနှင့် အိမ်ခြံမြေစျေးနှုန်းကြား ဆက်နွယ်မှုကို နားလည်လိုသည်ဆိုကြပါစို့။ ဤဆက်ဆံရေးကို ခွဲခြမ်းစိတ်ဖြာရန်၊ သီးခြားမြို့တစ်ခုရှိ အိမ် ၂၀၀ ၏ စတုရန်းပုံနှင့် ဈေးနှုန်းဆိုင်ရာ အချက်အလက်များကို စုဆောင်းသည်။

ဤအခြေအနေတွင်၊ အိမ်ခြံမြေအေးဂျင့်သည် ခန့်မှန်းသူကိန်းရှင် (စတုရန်းပုံ) သည် ဆက်တိုက်ဖြစ်နေသောကြောင့် ဤကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို ပိုင်းခြားစိတ်ဖြာရန် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုသင့်သည်။

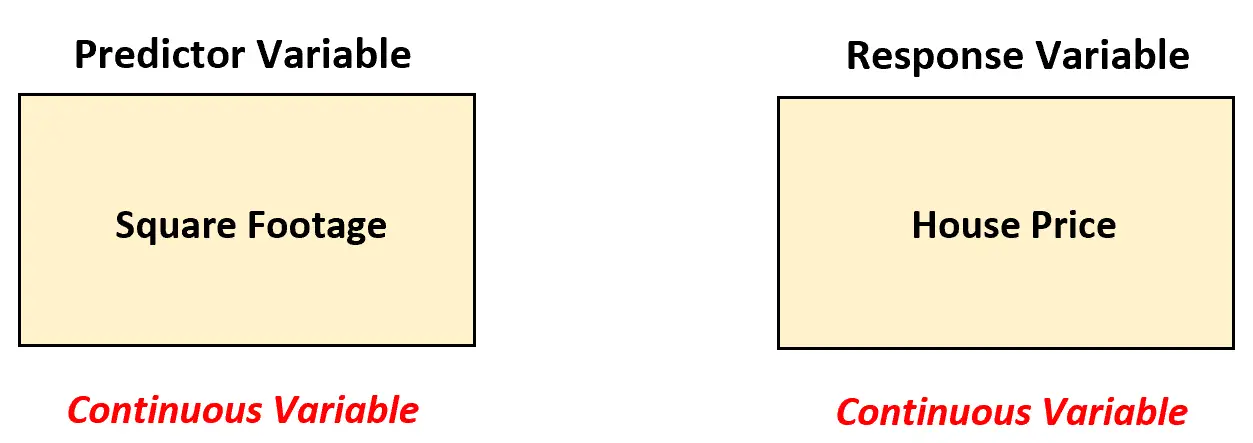
ရိုးရှင်းသော linear regression ကိုအသုံးပြုခြင်းဖြင့်၊ အိမ်ခြံမြေအေးဂျင့်သည် အောက်ဖော်ပြပါ ဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီနိုင်သည်-

အိမ်ခြံမြေစျေးနှုန်း = β ₀ + β ₁ (စတုရန်းဧရိယာ)

β ₁ ၏တန်ဖိုးသည် ထပ်လောင်းစတုရန်းပေတစ်ခုစီနှင့်ဆက်စပ်နေသော အိမ်စျေးနှုန်း၏ပျမ်းမျှပြောင်းလဲမှုကိုကိုယ်စားပြုမည်ဖြစ်သည်။

ယင်းက အိမ်ခြံမြေအကျိုးဆောင်သည် စတုရန်းပုံနှင့် အိမ်ခြံမြေစျေးနှုန်းကြား ဆက်နွယ်မှုကို တွက်ချက်နိုင်စေမည်ဖြစ်သည်။

ဥပမာ 3- နှစ်သက်သော ကိန်းဂဏန်းများပါရှိသော ဆုတ်ယုတ်မှုပုံစံ

အိမ်ခြံမြေအကျိုးဆောင်တစ်ဦးသည် အိမ်ခြံမြေစျေးနှုန်း၏ တုံ့ပြန်မှုပြောင်းလဲနိုင်သော “ စတုရန်းပုံ” နှင့် “ အိမ်အမျိုးအစား” (မိသားစုတစ်စု၊ တိုက်ခန်း၊ မြို့တော်အိမ်) တို့အကြား ဆက်စပ်မှုကို နားလည်လိုသည်ဆိုပါစို့။

ဤအခြေအနေမျိုးတွင်၊ အိမ်ခြံမြေအေးဂျင့်သည် လက်ရှိတွင် အမျိုးအစားခွဲကွဲပြားသည့်ကိန်းရှင်တစ်ခုဖြစ်သောကြောင့် “ အိမ်အမျိုးအစား” ကို dummy variable အဖြစ်သို့ပြောင်းခြင်းဖြင့်၊ အိမ်ခြံမြေအေးဂျင့်သည် မျဉ်းကြောင်းအတိုင်းဆုတ်ယုတ်မှုများစွာကို အသုံးပြုနိုင်သည်။

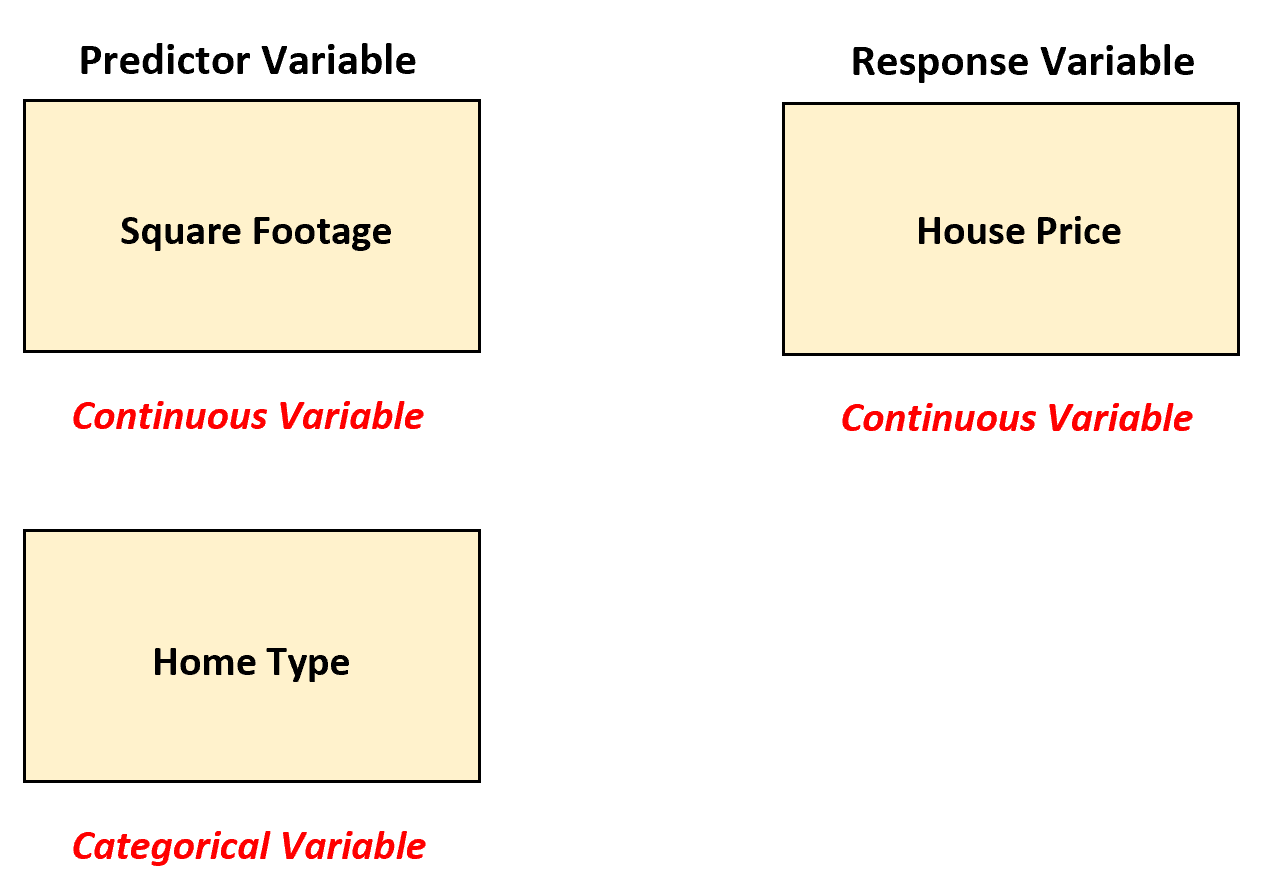
ထို့နောက် အိမ်ခြံမြေအေးဂျင့်သည် အောက်ဖော်ပြပါ မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုပုံစံမျိုးစုံကို ကိုက်ညီနိုင်သည်-

အိမ်ခြံမြေစျေးနှုန်း = β ₀ + β ₁ (စတုရန်းဧရိယာ) + β ₂ (မိသားစုတစ်စု) + β ₃ (တိုက်ခန်း)

ဤတွင် ကျွန်ုပ်တို့သည် မော်ဒယ် coefficients ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုမည်နည်း။

• β ₁ : နောက်ထပ် တစ်စတုရန်းပေနှင့် ဆက်စပ်နေသော အိမ်စျေးနှုန်း ပျမ်းမျှပြောင်းလဲမှု။
• β ₂ : စတုရန်းပုံတစ်ပုံသည် အဆက်မပြတ်ရှိနေသည်ဟု ယူဆရသည့် မိသားစုတစ်စုအိမ်နှင့် မြိုအိမ်ကြား ပျမ်းမျှစျေးနှုန်းကွာခြားချက်။
• β ₃ : မျက်နှာပြင်အကျယ်အဝန်းကို အဆက်မပြတ်ဟုယူဆကာ မိသားစုတစ်စုအိမ်နှင့် တိုက်ခန်းအကြား ပျမ်းမျှစျေးနှုန်းကွာခြားချက်။

မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲလ်တွင် dummy ကိန်းရှင်များကို ဖန်တီးနည်းကို ကြည့်ရှုရန် အောက်ပါသင်ခန်းစာများကို ကြည့်ပါ။

• R တွင် dummy variable များကိုဖန်တီးနည်း
• Excel တွင် Dummy Variable များကိုဖန်တီးနည်း

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ANOVA မော်ဒယ်များအတွက် အတွင်းကျကျ နိဒါန်းကို ပေးဆောင်သည်-

• One-Way ANOVA မိတ်ဆက်
• Two-Way ANOVA မိတ်ဆက်

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် linear regression ပုံစံများကို အတွင်းကျကျ နိဒါန်းပေးသည်-

• Simple Linear Regression နိဒါန်း
• Multiple Linear Regression အကြောင်း နိဒါန်း