Anova models အတွက် null hypothesis ကို နားလည်ခြင်း။

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သောအုပ်စုများ၏ နည်းလမ်းများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

တစ်လမ်းသွား ANOVA သည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည်-

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (အုပ်စုအားလုံးသည် တူညီသည်)
• H _A : အနည်းဆုံး အုပ်စုတစ်ခု၏ ပျမ်းမျှသည် မတူညီပါ။   အနားယူပါ။

ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်သင့်သည် သို့မဟုတ် မဆုံးဖြတ်ရန်၊ ANOVA ဇယားရလဒ်ရှိ p-value ကို ကိုးကားရန် လိုအပ်သည်။

p-value သည် အချို့သော အရေးပါမှုအဆင့် (ဥပမာ 0.05) အောက်တွင် ရှိနေပါက null hypothesis ကို ငြင်းပယ်နိုင်ပြီး အုပ်စုအားလုံးသည် တူညီသည်မဟုတ်ကြောင်း ကောက်ချက်ချနိုင်ပါသည်။

နှစ်လမ်းသွား ANOVA ကို ကိန်း ရှင်နှစ်ခုအတွက် သတ်မှတ်ပေးထားသော လွတ်လပ်သောအုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည် (တစ်ခါတစ်ရံ “ factors” ဟုခေါ်သည်)။

နှစ်လမ်းသွား ANOVA သည် null hypotheses သုံးခုကို တစ်ပြိုင်နက်တည်း စမ်းသပ်သည်-

• အုပ်စုဟူသည်အားလုံးသည် ပထမကိန်းရှင်အဆင့်တစ်ခုစီတွင် တန်းတူဖြစ်သည်။
• အုပ်စုဟူသည်အားလုံးသည် ဒုတိယကိန်းရှင်အဆင့်တစ်ခုစီတွင် တူညီပါသည်။
• ကိန်းရှင်နှစ်ခုကြားတွင် အပြန်အလှန်သက်ရောက်မှုမရှိပါ။

ကျွန်ုပ်တို့သည် null hypothesis တစ်ခုစီကို ငြင်းပယ်သင့်မသင့် ဆုံးဖြတ်ရန်၊ two-way ANOVA table ၏ရလဒ်တွင် p-values များကို ကိုးကားရန် လိုအပ်သည်။

အောက်ဖော်ပြပါနမူနာများသည် တစ်ကြောင်း ANOVA နှင့် two-way ANOVA တွင် null hypothesis ကို ငြင်းပယ်ခြင်း ရှိ၊မရှိ ဆုံးဖြတ်နည်းကို ပြသသည်။

ဥပမာ 1- တစ်လမ်းမောင်း ANOVA

မတူညီသော စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်သုံးခုသည် ပေးထားသော စာမေးပွဲတစ်ခုတွင် မတူညီသော ပျမ်းမျှရမှတ်များ ဖြစ်ပေါ်လာခြင်း ရှိ၊မရှိ သိလိုသည်ဆိုပါစို့။ ဤအရာကို စမ်းသပ်ရန်အတွက် ကျွန်ုပ်တို့သည် လေ့လာမှုတစ်ခုတွင် ပါဝင်ရန် ကျောင်းသား 30 ကို စုဆောင်းပြီး ၎င်းတို့ကို အုပ်စုသုံးစုခွဲထားသည်။

အုပ်စုတစ်ခုစီရှိ ကျောင်းသားများသည် စာမေးပွဲအတွက် ပြင်ဆင်ရန် အောက်ပါသုံးပတ်အတွက် စာမေးပွဲပြင်ဆင်မှု ပရိုဂရမ်သုံးခုထဲမှ တစ်ခုကို အသုံးပြုရန် ကျပန်းသတ်မှတ်ပေးထားသည် ။ သုံးပတ်အဆုံးတွင် ကျောင်းသားအားလုံး စာမေးပွဲကို အတူတူဖြေဆိုကြသည်။

အုပ်စုတစ်ခုစီအတွက် စာမေးပွဲရလဒ်များကို အောက်တွင် ဖော်ပြထားသည်။

ကျွန်ုပ်တို့သည် ဤတန်ဖိုးများကို တစ်လမ်းသွား ANOVA ဂဏန်းတွက်စက် ထဲသို့ ထည့်သွင်းသောအခါ၊ ကျွန်ုပ်တို့သည် အောက်ပါ ANOVA ဇယားကို အထွက်အဖြစ် လက်ခံရရှိသည်-

p-value သည် 0.11385 ဖြစ်ကြောင်း သတိပြုပါ။

ဤအထူးဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုပါမည်။

• H ₀ : μ ₁ = μ ₂ = μ ₃ (အုပ်စုတစ်ခုစီအတွက် ပျမ်းမျှ စာမေးပွဲရမှတ် ညီမျှသည်)
• H _A : အနည်းဆုံး အုပ်စုတစ်ခု၏ ပျမ်းမျှသည် မတူညီပါ။   အနားယူပါ။

ANOVA ဇယား၏ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။

ဆိုလိုသည်မှာ အုပ်စုသုံးစု၏ ပျမ်းမျှစာမေးပွဲရမှတ်များကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားမရှိဟု ဆိုလိုပါသည်။

ဥပမာ 2- နှစ်လမ်းသွား ANOVA

ရုက္ခဗေဒပညာရှင်တစ်ဦးသည် နေရောင်ခြည်နှင့် ထိတွေ့မှုအကြိမ်ရေကြောင့် အပင်ကြီးထွားမှုအပေါ် လွှမ်းမိုးမှုရှိမရှိ သိချင်သည်ဆိုပါစို့။

အစေ့အစေ့ ၄၀ ကို စိုက်ပျိုးပြီး နေရောင်ခြည်နှင့် ရေလောင်းအကြိမ်ရေ မတူညီသော အခြေအနေများတွင် နှစ်လကြာ ကြီးထွားစေပါသည်။ နှစ်လကြာပြီးနောက် အပင်တစ်ပင်ချင်းစီ၏ အမြင့်ကို မှတ်တမ်းတင်သည်။ ရလဒ်များကို အောက်တွင် ပြထားသည်။

အထက်ဖော်ပြပါဇယားတွင် အပင်ငါးပင်ကို အခြေအနေတစ်ခုစီတွင် ပေါင်းစပ်စိုက်ပျိုးထားကြောင်း တွေ့ရပါသည်။

ဥပမာအားဖြင့် အပင်ငါးပင်ကို နေ့စဥ်ရေလောင်းပြီး နေရောင်မရှိသဖြင့် နှစ်လအကြာတွင် အမြင့်မှာ ၄.၈ လက်မ၊ ၄.၄ လက်မ၊ ၃.၂ လက်မ၊ ၃.၉ လက်မနှင့် ၄.၄ လက်မ၊

သူမသည် Excel တွင် နှစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်ပြီး အောက်ပါရလဒ်ကို ရရှိသည် ။

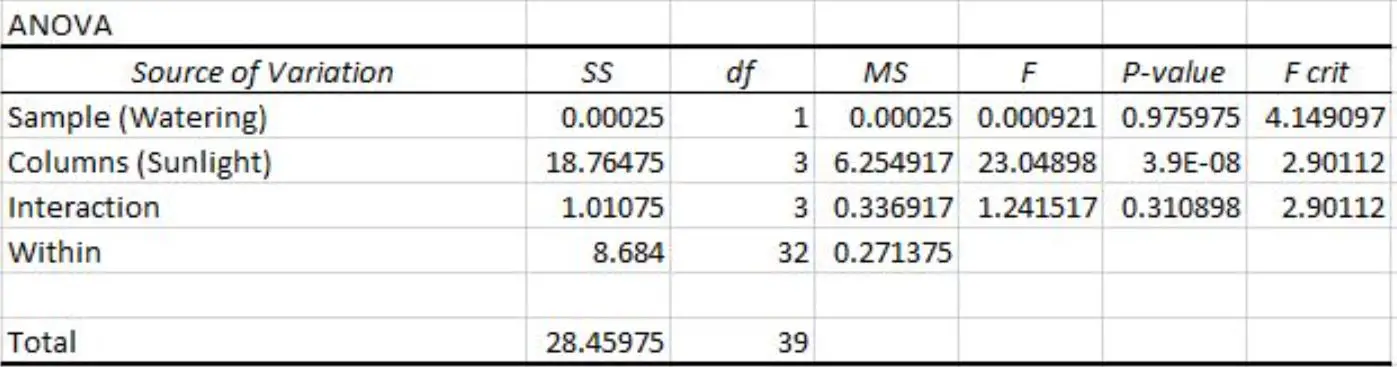
နှစ်လမ်း ANOVA ဇယားရလဒ်တွင် အောက်ပါ p-တန်ဖိုးများကို ကျွန်ုပ်တို့ မြင်နိုင်သည်-

• ရေလောင်းအကြိမ်ရေအတွက် p-တန်ဖိုးသည် 0.975975 ဖြစ်သည်။ ၎င်းသည် 0.05 အရေးပါမှုအဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်မဟုတ်ပါ။
• နေရောင်ခြည်ထိတွေ့မှုအတွက် p-တန်ဖိုးသည် 3.9E-8 (0.000000039) ဖြစ်သည်။ ၎င်းသည် 0.05 အရေးပါမှုအဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။
• ရေလောင်းအကြိမ်ရေနှင့် နေရောင်ခြည်ထိတွေ့မှုကြား အပြန်အလှန်အကျိုးသက်ရောက်မှုအတွက် p-တန်ဖိုးသည် 0.310898 ဖြစ်သည်။ ၎င်းသည် 0.05 အရေးပါမှုအဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်မဟုတ်ပါ။

ဤရလဒ်များသည် အပင်အမြင့်အပေါ် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော အကျိုးသက်ရောက်မှုရှိသော တစ်ခုတည်းသောအချက်မှာ နေရောင်ခြည်နှင့်ထိတွေ့ခြင်းဖြစ်သည်ဟု ဖော်ပြသည်။

အပြန်အလှန်အကျိုးသက်ရောက်မှုမရှိသောကြောင့်၊ နေရောင်ခြည်ထိတွေ့မှုအကျိုးသက်ရောက်မှုသည် ရေလောင်းအကြိမ်ရေအဆင့်တိုင်းတွင် တသမတ်တည်းဖြစ်သည်။

ရိုးရိုးရှင်းရှင်းပြောရလျှင် အပင်တစ်ပင်ကို နေ့စဉ် သို့မဟုတ် အပတ်စဉ် ရေလောင်းသည်ဖြစ်စေ နေရောင်ထိတွေ့မှုသည် အပင်အပေါ် သက်ရောက်မှုမရှိပေ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါသင်ခန်းစာများသည် ANOVA မော်ဒယ်များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

ANOVA တွင် F တန်ဖိုးနှင့် P တန်ဖိုးကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုမည်နည်း။
ANOVA တွင် စတုရန်း၏ပေါင်းလဒ်ကို တွက်နည်း
ANOVA တွင် မြင့်မားသော F တန်ဖိုးဟူသည် အဘယ်နည်း။