Anova ထပ်ခါတလဲလဲ အစီအမံများကို ကိုယ်တိုင်လုပ်ဆောင်နည်း
အုပ်စုတစ်ခုစီတွင် တူညီသောဘာသာရပ်များပေါ်လာသည့် အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသောအုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသောခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် ထပ်ခါတလဲလဲတိုင်းတာမှုများကို ANOVA ကို အသုံးပြုသည်။
ဤသင်ခန်းစာတွင် ANOVA တစ်လမ်းသွား ထပ်ခါတလဲလဲ တိုင်းတာနည်းကို ကိုယ်တိုင်လုပ်ဆောင်ပုံကို ရှင်းပြထားသည်။
ဥပမာ- တစ်လမ်းမောင်း ANOVA ကို လက်ဖြင့် တိုင်းတာသည်။
မတူညီသော ဆေးဝါးသုံးမျိုးသည် မတူညီသော တုံ့ပြန်မှုအကြိမ်များကို ဖြစ်စေကြောင်း သုတေသီများက သိချင်ကြသည်။ ၎င်းကိုစမ်းသပ်ရန်၊ ၎င်းတို့သည် ဆေးတစ်ခုစီသို့ လူနာငါးဦး၏ တုံ့ပြန်မှုအချိန် (စက္ကန့်ပိုင်း) ကို တိုင်းတာသည်။ ရလဒ်များကို အောက်တွင် ပြထားသည်။
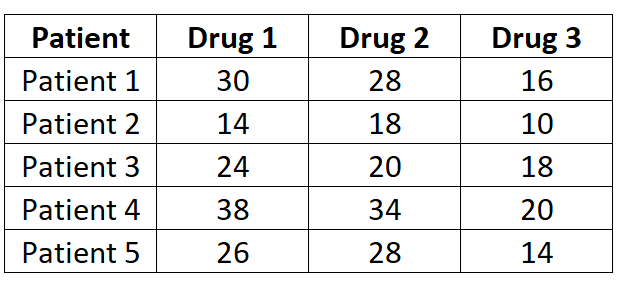
လူနာတစ်ဦးစီသည် ဆေးဝါးသုံးမျိုးမှ တစ်ခုစီကို တိုင်းတာသောကြောင့်၊ ဆေးဝါးများကြား ပျမ်းမျှတုံ့ပြန်မှုအချိန်ကွာခြားခြင်းရှိမရှိကို ဆုံးဖြတ်ရန် တစ်ကြောင်းတည်းသော ထပ်ခါတလဲလဲတိုင်းတာမှုများ ANOVA ကို အသုံးပြုပါမည်။
ANOVA ထပ်ခါတလဲလဲ တိုင်းတာမှုများကို ကိုယ်တိုင်လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို လိုက်နာပါ-
အဆင့် 1- SST ကို တွက်ချက်ပါ။
ပထမဦးစွာ၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွေ့ရှိနိုင်သည့် စုစုပေါင်းစတုရန်းများ (SST) ကို တွက်ချက်ပါမည်။
SST = s 2 စုစုပေါင်း (n စုစုပေါင်း -1)
ရွှေ-
- s 2 စုစုပေါင်း – ဒေတာအတွဲအတွက် ကွဲလွဲမှု
- n စုစုပေါင်း : ဒေတာအတွဲတွင် ကြည့်ရှုမှုစုစုပေါင်း
ဤဥပမာတွင်၊ ကျွန်ုပ်တို့ SST ကို အောက်ပါအတိုင်း တွက်ချက်သည်- (64.2667)(15-1) = 899.7
အဆင့် 2- SSB တွက်ချက်ပါ။
ထို့နောက်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွေ့ရှိနိုင်သည့် စတုရန်းပေါင်းလဒ် (SSB) ကို တွက်ချက်ပါမည်။
SSB = Σn j ( x j – x စုစုပေါင်း ) ၂
ရွှေ-
- Σ : “ ပေါင်း” ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
- n j : j th အုပ်စုရှိ စုစုပေါင်း စောင့်ကြည့်မှု အရေအတွက်
- x j : jth အုပ်စု၏ ပျမ်းမျှ
- x စုစုပေါင်း : ဒေတာအားလုံး၏ ပျမ်းမျှ
ဤဥပမာတွင်၊ ကျွန်ုပ်တို့ SSB ကို အောက်ပါအတိုင်း တွက်ချက်သည်- (5)(26.4-22.533) 2 +(5)(25.6-22.533) 2 + (5)(15.6-22.533) 2 = 362.1
အဆင့် 3- SSS ကို တွက်ချက်ပါ။
ထို့နောက်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွေ့ရှိနိုင်သည့် ဘာသာရပ်ပေါင်းလဒ် (SSS) ကို တွက်ချက်ပါမည်။
SSS =(Σr 2 k /c) – (N 2 /rc)
ရွှေ-
- Σ : “ ပေါင်း” ဟု အဓိပ္ပာယ်ရသော ဂရိသင်္ကေတ
- r 2 k : kth လူနာ၏ နှစ်ထပ်ကိန်း
- N- ဒေတာအားလုံး၏ ကြီးကျယ်သော စုစုပေါင်း
- r: စုစုပေါင်းလူနာအရေအတွက်
- c: စုစုပေါင်းအဖွဲ့အရေအတွက်
ဤဥပမာတွင်၊ ကျွန်ုပ်တို့ SSS ကို အောက်ပါအတိုင်း တွက်ချက်သည်- ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441.1
အဆင့် 4- SES တွက်ချက်ပါ။
ထို့နောက်၊ အောက်ပါဖော်မြူလာကိုအသုံးပြု၍ တွေ့ရှိနိုင်သည့် နှစ်ထပ်အမှားအယွင်း (SSE) ၏ပေါင်းလဒ်ကို တွက်ချက်ပါမည်။
SSE = SST – SSB – SSS
ဤဥပမာတွင်၊ SES ကို အောက်ပါအတိုင်း တွက်ချက်ပါသည်- 899.7 – 362.1 – 441.1 = 96.5
အဆင့် 5- ထပ်ခါတလဲလဲ တိုင်းတာမှုများ ANOVA ဇယားကို ဖြည့်ပါ။
ယခု ကျွန်ုပ်တို့တွင် SSB၊ SSS နှင့် SSE ရှိသည်ဖြစ်သောကြောင့် ထပ်ခါတလဲလဲ တိုင်းတာမှုများ ANOVA ဇယားကို ဖြည့်သွင်းနိုင်သည်-
| အရင်းအမြစ် | စတုရန်းများပေါင်း (SS) | df | ပျမ်းမျှစတုရန်းများ (MS) | F |
|---|---|---|---|---|
| အကြား | ၃၆၂.၁ | ၂ | 181.1 | ၁၅,၀၀၆ |
| ဘာသာရပ် | ၄၄၁.၁ | ၄ | ၁၁၀.၃ | |
| အမှား | ၉၆.၅ | ၈ | ၁၂.၁ |
ဤသည်မှာ ဇယားရှိ မတူညီသော ဂဏန်းများကို တွက်ချက်ပုံ ဖြစ်ပါသည်။
- df အကြား- #groups – 1 = 3 – 1 = 2
- df ဘာသာရပ်- #participants – 1 = 5 – 1 = 4
- df အမှား- * df အကြောင်းအရာ = 2*4 = 8 ကြား df
- MS ဝင်သည်- SSB / df ဝင်ရောက်သည် = 362.1 / 2 = 181.1
- MS ဘာသာရပ်- SSS ဘာသာရပ် / df = 441.1 / 4 = 110.3
- MS အမှား- SSE အမှား / df = 96.5 / 8 = 12.1
- F- MS ဝင်သည် / MS အမှား = 181.1 / 12.1 = 15.006
အဆင့် 6: ရလဒ်များကို ဘာသာပြန်ပါ။
ဤတစ်လမ်းသွား ထပ်ခါတလဲလဲ တိုင်းတာမှုများအတွက် F စစ်ဆေးမှု ကိန်းဂဏန်းသည် 15.006 ဖြစ်သည်။ ၎င်းသည် ကိန်းဂဏန်းအချက်အလက်များအရ သိသာထင်ရှားသောရလဒ်ဟုတ်မဟုတ် ဆုံးဖြတ်ရန်၊ ၎င်းကို F ဖြန့်ဖြူးမှုဇယား တွင် တွေ့ရှိရသည့် အရေးကြီးသော F တန်ဖိုးနှင့် နှိုင်းယှဉ်ရန် လိုအပ်သည် –
- α (အရေးပါမှုအဆင့်) = 0.05
- DF1 (ပိုင်းဝေ၏လွတ်လပ်မှုဒီဂရီ) = df အကြား = 2
- DF2 (ပိုင်းခြေ၏လွတ်လပ်မှုဒီဂရီ) = အမှား df = 8
F ၏ အရေးပါသောတန်ဖိုးမှာ 4.459 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့ရှိရပါသည်။
ANOVA ဇယားရှိ F စမ်းသပ်မှုကိန်းဂဏန်းသည် F ဖြန့်ဖြူးမှုဇယားရှိ အရေးပါသောတန်ဖိုး F ထက် ကြီးသောကြောင့်၊ ကျွန်ုပ်တို့သည် null အယူအဆကို ငြင်းပယ်ပါသည်။ ဆိုလိုသည်မှာ ဆေးဝါးများ၏ ပျမ်းမျှတုံ့ပြန်မှုအကြိမ်များကြားတွင် စာရင်းအင်းအရ သိသာထင်ရှားသော ခြားနားချက်ရှိသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားများရှိသည်။