လမ်းညွှန်ချက်အပြည့်အစုံ- sas တွင် anova ရလဒ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုမည်နည်း။
တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။
အောက်ပါဥပမာသည် SAS ရှိ one-way ANOVA ၏ရလဒ်များကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို ပြသထားသည်။
ဥပမာ- ANOVA ရလဒ်များကို SAS တွင် ဘာသာပြန်ခြင်း။
သုတေသီတစ်ဦးသည် လေ့လာမှုတစ်ခုတွင် ပါဝင်ရန် ကျောင်းသား 30 ကို ခေါ်ယူသည်ဆိုပါစို့။ ကျောင်းသားများကို စာမေးပွဲအတွက် ပြင်ဆင်ရန် လေ့လာမှုနည်းလမ်း သုံးခုအနက်မှ တစ်ခုကို အသုံးပြုရန် ကျပန်းသတ်မှတ်ထားသည် ။
ကျောင်းသားတစ်ဦးစီအတွက် စာမေးပွဲရလဒ်များကို အောက်တွင် ဖော်ပြထားသည်။

SAS တွင် ဤဒေတာအတွဲကို ဖန်တီးရန် အောက်ပါကုဒ်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။
/*create dataset*/
data my_data;
input Method $Score;
datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;
ထို့နောက် တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ရန် proc ANOVA ကို အသုံးပြုပါမည်။
/*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;
မှတ်ချက် – တစ်လမ်းသွား ANOVA မှ ကိန်းဂဏန်း အရ သိသာထင်ရှားသော p-value သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါက Tukey post-hoc စစ်ဆေးမှုအား (ယုံကြည်မှုရှိသော ကြားကာလများနှင့်အတူ) သတ်မှတ်ရန် tukey နှင့် cldiff ရွေးချယ်မှုများနှင့်အတူ အဓိပ္ပါယ်ဖော်ပြချက်အား ကျွန်ုပ်တို့အသုံးပြုထားပါသည်။
ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် ANOVA ဇယားကိုကြည့်မည်၊

ဤသည်မှာ output တွင် တန်ဖိုးတစ်ခုစီကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ဖြစ်သည် ။
DF မော်ဒယ်- ပြောင်းလဲနိုင်သော နည်းလမ်း အတွက် လွတ်လပ်မှုဒီဂရီများ။ ၎င်းကို #groups -1 အဖြစ် တွက်ချက်သည်။ ဤကိစ္စတွင်၊ ကွဲပြားသောလေ့လာမှုနည်းလမ်း 3 ခုရှိသောကြောင့် ဤတန်ဖိုးသည် 3-1 = 2 ဖြစ်သည်။
DF အမှား- အကြွင်းအကျန်များအတွက် လွတ်လပ်မှုဒီဂရီ။ ၎င်းကို #စုစုပေါင်း လေ့လာတွေ့ရှိချက်များ – #groups အဖြစ် တွက်ချက်သည်။ ဤကိစ္စတွင်၊ ရှုမြင်မှု 24 ခုနှင့် အုပ်စု 3 ခုရှိသည်၊ ထို့ကြောင့် ဤတန်ဖိုးသည် 24-3 = 21 ဖြစ်သည်။
ပြုပြင်ထားသော စုစုပေါင်း – DF မော်ဒယ်၏ ပေါင်းလဒ်နှင့် DF အမှား။ ဤတန်ဖိုးသည် 2 + 21 = 23 ဖြစ်သည်။
Sum of Squares Model- ပြောင်းလဲနိုင်သော နည်းလမ်း နှင့်ဆက်စပ်သော လေးထောင့်၏ပေါင်းလဒ်။ ဤတန်ဖိုးသည် 175.583 ဖြစ်သည်။
Sum of Squares အမှား- အကြွင်းအကျန်များ သို့မဟုတ် “ အမှားများ” နှင့်ဆက်စပ်သော လေးထောင့်ပေါင်းစု။ ဤတန်ဖိုးသည် 350.25 ဖြစ်သည်။
ပြုပြင်ထားသော လေးထောင့်စုစုပေါင်း : SS မော်ဒယ်၏ ပေါင်းလဒ်နှင့် SS အမှား။ ဤတန်ဖိုးသည် 525.833 ဖြစ်သည်။
Mean squares မော်ဒယ်- method နှင့်ဆက်စပ်နေသော လေးထောင့်ကိန်းများကို ဆိုလိုသည်။ ၎င်းကို SS မော်ဒယ် / DF မော်ဒယ်အဖြစ် တွက်ချက်သည်၊ သို့မဟုတ် 175.583 / 2 = 87.79 ဖြစ်သည်။
ပျမ်းမျှ နှစ်ထပ်အမှားအယွင်း- အကြွင်းများနှင့် ဆက်စပ်နေသော နှစ်ထပ်ကိန်းများ ပျမ်းမျှ။ ၎င်းကို 350.25/21 = 16.68 ဖြစ်သည့် SS Error/DF Error အဖြစ် တွက်ချက်သည်။
F တန်ဖိုး- ANOVA မော်ဒယ်၏ စုစုပေါင်း F စာရင်းအင်း။ ၎င်းကို model mean square/mean square အမှားအဖြစ် တွက်ချက်သည်၊ သို့မဟုတ် 87.79/16.68 = 5.26 ဖြစ်သည် ။
Pr >F- ပိုင်းဝေ df = 2 နှင့် ပိုင်းခြေ df = 21 နှင့် F ကိန်းဂဏာန်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုး။ ဤကိစ္စတွင်၊ p-တန်ဖိုးသည် 0.0140 ဖြစ်သည်။
ရလဒ်အစုတွင် အရေးကြီးဆုံးတန်ဖိုးမှာ p-value ဖြစ်ပြီး၊ အဘယ်ကြောင့်ဆိုသော် ၎င်းသည် အုပ်စုသုံးစုကြား ပျမ်းမျှတန်ဖိုးများတွင် သိသာထင်ရှားစွာ ကွာခြားမှုရှိမရှိကို ပြောပြသောကြောင့်ဖြစ်သည်။
တစ်လမ်းသွား ANOVA သည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုကြောင်း သတိရပါ။
- H 0 (null hypothesis): အုပ်စုဟူသည် အားလုံး ညီတူညီမျှဖြစ်သည်။
- H A (အခြားသောယူဆချက်)- အနည်းဆုံးအုပ်စုတစ်ခု၏ပျမ်းမျှသည် အခြားအုပ်စုများနှင့်မတူပါ။
ကျွန်ုပ်တို့၏ ANOVA ဇယားရှိ p-တန်ဖိုး (0.0140) သည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။
ဆိုလိုသည်မှာ လေ့လာမှုနည်းလမ်းသုံးခုတွင် ပျမ်းမျှစာမေးပွဲရမှတ်သည် ညီမျှခြင်းမရှိဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။
မည်သည့်အဖွဲ့၏ အဓိပ္ပါယ်သည် ကွဲပြားသည်ကို အတိအကျ ဆုံးဖြတ်ရန်၊ Tukey ၏ post-hoc စာမေးပွဲများ၏ ရလဒ်များကို ပြသသည့် နောက်ဆုံးရလဒ်ဇယားကို ကိုးကားရန် လိုအပ်သည်-
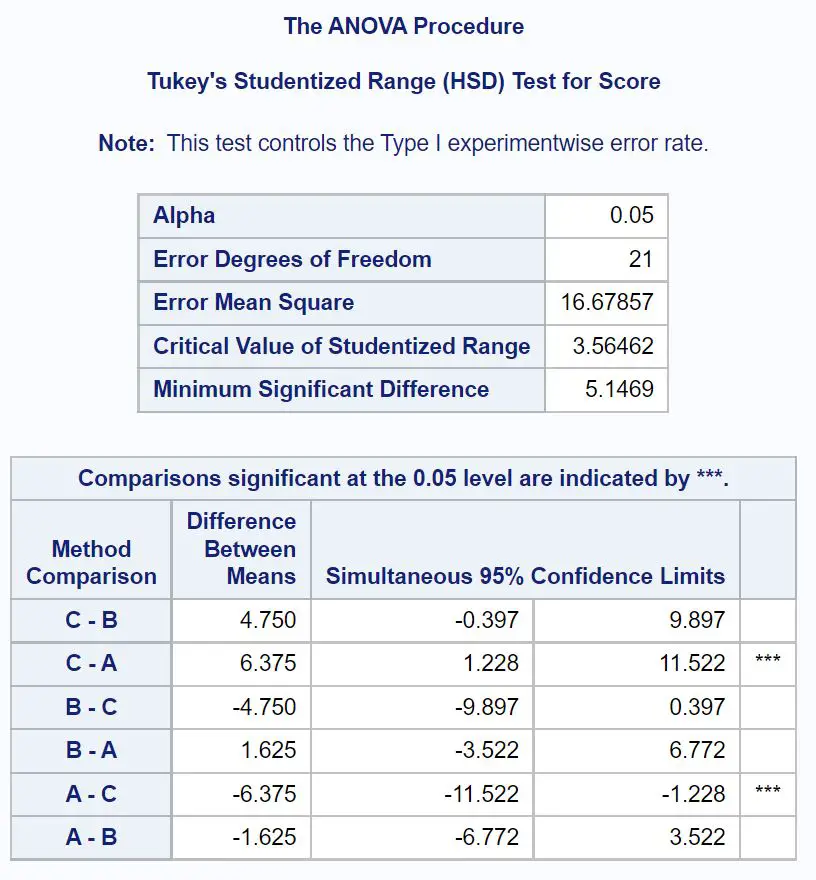
ဘယ်အဖွဲ့ရဲ့ အဓိပ္ပါယ်က ကွာခြားလဲဆိုတာကို သိချင်ရင် သူတို့ဘေးမှာ ကြယ်တွေ ( *** ) ပါနေတဲ့ အတွဲလိုက် နှိုင်းယှဉ်မှုတွေကို ကြည့်ဖို့ လိုပါတယ်။
Group A နှင့် Group C အကြား ပျမ်းမျှ စာမေးပွဲရမှတ်များတွင် ကိန်းဂဏန်း သိသိသာသာ ကွာခြားချက်ရှိကြောင်း ဇယားတွင် ပြသထားသည်။
အထူးသဖြင့်၊ Group C နှင့် Group A ကြားရှိ စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှကွာခြားချက်မှာ 6.375 ဖြစ်သည်။
ပျမ်းမျှကွာခြားချက်အတွက် 95% ယုံကြည်မှုကြားကာလသည် [1.228၊ 11.522] ဖြစ်သည်။
အခြားအုပ်စုများ၏ နည်းလမ်းများကြားတွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ကွာခြားချက်မရှိပါ။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ပါသင်ခန်းစာများသည် ANOVA မော်ဒယ်များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-
ANOVA ဖြင့် Post-Hoc Testing ကိုအသုံးပြုခြင်းလမ်းညွှန်
SAS တွင် one-way ANOVA လုပ်ဆောင်နည်း
SAS တွင် နှစ်လမ်းသွား ANOVA လုပ်ဆောင်နည်း