R တွင် skewness & kurtosis တွက်နည်း

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ လွဲမှားမှု နှင့် kurtosis သည် ဖြန့်ဖြူးမှုပုံသဏ္ဍာန်ကို တိုင်းတာသည့် နည်းလမ်းနှစ်သွယ်ဖြစ်သည်။

Skewness သည် ဖြန့်ဝေမှုတစ်ခု၏ ပေါ့ပါးမှု၏ အတိုင်းအတာတစ်ခုဖြစ်သည်။ ဤတန်ဖိုးသည် အပေါင်း သို့မဟုတ် အနုတ်လက္ခဏာ ဖြစ်နိုင်သည်။

• အနုတ်လက္ခဏာ လွဲချော်နေခြင်းက အမြီးသည် ဖြန့်ဖြူးမှု၏ ဘယ်ဘက်ခြမ်းတွင် ရှိနေကြောင်း ညွှန်ပြသည်၊ ၎င်းသည် ပို၍ အနုတ်လက္ခဏာတန်ဖိုးများဆီသို့ တိုးသွားပါသည်။
• အပြုသဘောဆောင်သော လှည့်ကွက်သည် အမြီးသည် ဖြန့်ဖြူးမှု၏ ညာဘက်ခြမ်းတွင် ရှိနေကြောင်း ညွှန်ပြသည်၊ ၎င်းသည် ပိုမိုအပြုသဘောဆောင်သော တန်ဖိုးများဆီသို့ တိုးသွားပါသည်။
• သုည၏တန်ဖိုးသည် ဖြန့်ဖြူးမှုတွင် အချိုးမညီမှုမရှိကြောင်း ညွှန်ပြသည်၊ ဆိုလိုသည်မှာ ဖြန့်ဖြူးမှုသည် လုံးဝအချိုးကျသည်ဟု ဆိုလိုသည်။

Kurtosis သည် ပုံမှန်ဖြန့်ဖြူးမှု တစ်ခုနှင့် နှိုင်းယှဉ်ပါက လေးလံခြင်း သို့မဟုတ် အမြီးပျော့ခြင်းရှိမရှိကို တိုင်းတာခြင်းဖြစ်သည်။

• ပုံမှန်ဖြန့်ဖြူးမှု၏ kurtosis သည် 3 ဖြစ်သည်။
• ပေးထားသော ဖြန့်ဖြူးမှုတစ်ခုတွင် 3 ထက်နည်းသော kurtosis ရှိပါက ၎င်းကို playkurtic ဟု ဆိုသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် ပုံမှန်ဖြန့်ဖြူးမှုထက် ပိုနည်းပြီး အလွန်အမင်း လွန်ကဲသော အထွက်နှုန်းများကို ထုတ်ပေးတတ်သည်။
• ပေးထားသောဖြန့်ဖြူးမှုတစ်ခုတွင် 3 ထက်ကြီးသော kurtosis ရှိပါက၊ ၎င်းကို leptokurtic ဟုဆိုသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် ပုံမှန်ဖြန့်ဖြူးမှုထက် ပိုပိုသာလွန်ဖွယ်ရှိသည်ဟု ဆိုလိုသည်။

မှတ်ချက်- အချို့သော ဖော်မြူလာများ (Fisher အဓိပ္ပါယ်ဖွင့်ဆိုချက်) 3 ကို သာမာန်ဖြန့်ဖြူးမှုနှင့် နှိုင်းယှဉ်ရန် ပိုမိုလွယ်ကူစေရန် kurtosis မှ 3 ကို နုတ်ပါ။ ဤအဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို အသုံးပြုခြင်းဖြင့်၊ ဖြန့်ဖြူးမှုတစ်ခုတွင် kurtosis တန်ဖိုး 0 ထက်ကြီးပါက ပုံမှန်ဖြန့်ဖြူးမှုထက် kurtosis ပိုကြီးမည်ဖြစ်သည်။

ဤသင်ခန်းစာသည် R တွင်ပေးထားသောဒေတာအတွဲတစ်ခု၏ skewness နှင့် kurtosis နှစ်မျိုးလုံးကို တွက်ချက်နည်းကို ရှင်းပြထားသည်။

ဥပမာ- R တွင် ပေါ့ပါးခြင်းနှင့် ချောမွတ်ခြင်း

ကျွန်ုပ်တို့တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Histogram ဖန်တီးခြင်းဖြင့် ဤဒေတာအတွဲရှိ တန်ဖိုးများ ဖြန့်ဖြူးမှုကို ကျွန်ုပ်တို့ လျင်မြန်စွာ မြင်ယောင်နိုင်သည်-

 hist(data, col=' steelblue ') 

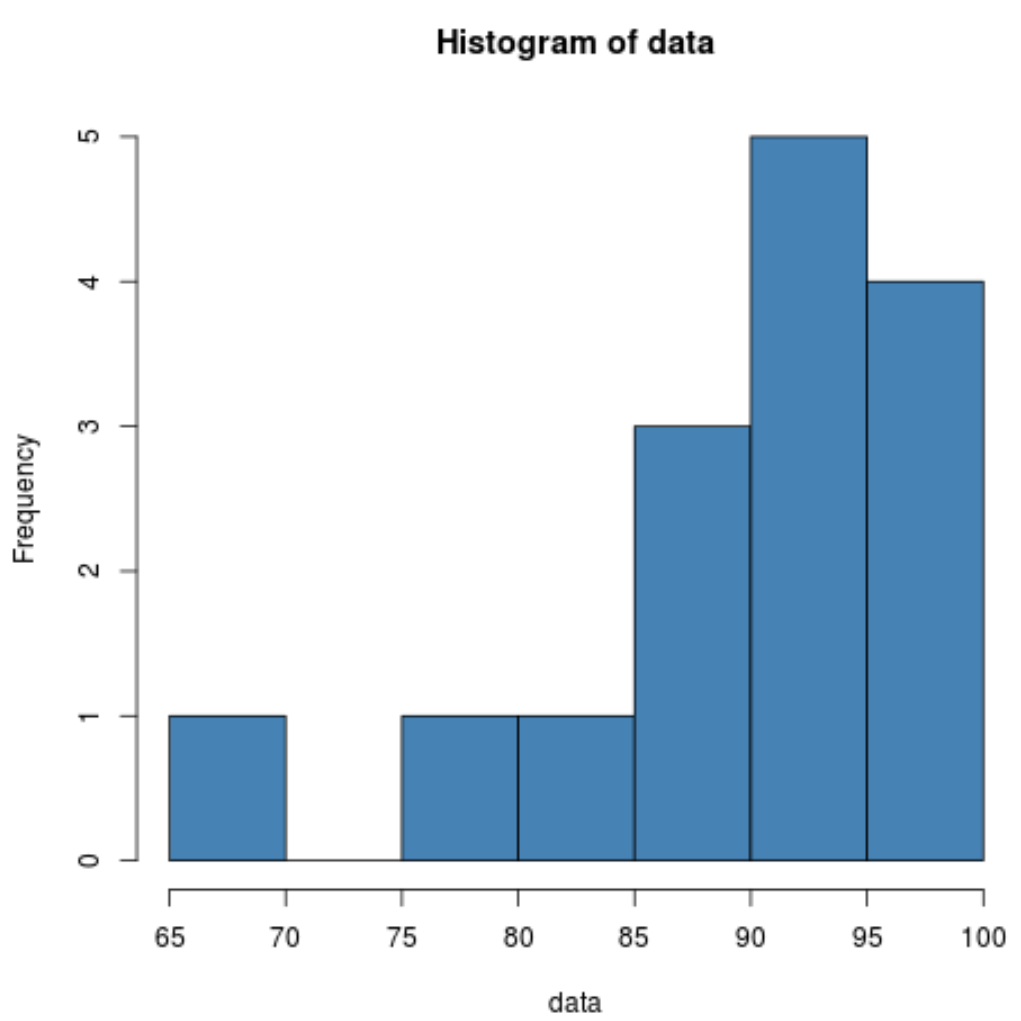
ဖြန့်ဖြူးမှုသည် ဘယ်ဘက်သို့ စောင်းနေပုံပေါ်ကြောင်း ဟီစတိုဂရမ်က ပြသသည်။ ဆိုလိုသည်မှာ၊ တန်ဖိုးများ၏ပိုကြီးသောအပိုင်းကို ဖြန့်ဖြူးမှု၏ညာဘက်ခြမ်းတွင် စုစည်းထားသည်။

ဤဒေတာအတွဲ၏ လွဲချော်မှုနှင့် kurtosis ကို တွက်ချက်ရန်၊ R ရှိ အခိုက်အတန့် စာကြည့်တိုက်မှ skewness() နှင့် kurtosis() လုပ်ဆောင်ချက်များကို အသုံးပြုနိုင်ပါသည်။

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

လွဲချော်မှုမှာ -1.391777 ဖြစ်လာပြီး kurtosis သည် 4.177865 ဖြစ်သွားသည်။

လွဲချော်မှုမှာ အနုတ်လက္ခဏာဖြစ်သောကြောင့်၊ ယင်းက ဖြန့်ဝေမှုမှာ လွဲချော်နေခြင်းကို ညွှန်ပြသည်။ ၎င်းသည် ဟီစတိုဂရမ်တွင် ကျွန်ုပ်တို့မြင်ခဲ့ရသည်ကို အတည်ပြုသည်။

kurtosis သည် 3 ထက် ကြီးသောကြောင့်၊ ၎င်းသည် ဖြန့်ဖြူးမှုတွင် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုနှင့် နှိုင်းယှဉ်ပါက အမြီးများတွင် တန်ဖိုးပိုများကြောင်း ညွှန်ပြသည်။

အခိုက်အတန့် စာကြည့်တိုက်တွင် နမူနာဒေတာသည် ပုံမှန်ဖြန့်ဝေမှုတစ်ခုနှင့် ကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ပေးသည့် ကောင်းမွန်သောစမ်းသပ်မှုတစ်ခုလုပ်ဆောင်သည့် jarque.test() လုပ်ဆောင်ချက်ကိုလည်း ပံ့ပိုးပေးပါသည်။ ဤစမ်းသပ်မှု၏ null နှင့် အခြားအခြားသော ယူဆချက်များမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

Null hypothesis- ဒေတာအစုံတွင် ပုံမှန်ဖြန့်ဝေမှုတစ်ခုနှင့် ကိုက်ညီသော skewness နှင့် kurtosis ရှိသည်။

အစားထိုးယူဆချက် – ဒေတာအတွဲတွင် ပုံမှန်ဖြန့်ဝေမှုတစ်ခုနှင့် မကိုက်ညီသည့် လွဲချော်မှုနှင့် kurtosis ရှိသည်။

အောက်ပါကုဒ်သည် ဤစမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

စာမေးပွဲ၏ p-value သည် 0.05756 ဖြစ်သွားသည်။ ဤတန်ဖိုးသည် α = 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ဤဒေတာအတွဲသည် သာမာန်ဖြန့်ဖြူးမှုနှင့်မတူဘဲ လွဲချော်နေပြီး kurtosis ရှိသည်ဟုဆိုရန် လုံလောက်သောအထောက်အထားမရှိပါ။

Moments Library စာရွက်စာတမ်းအပြည့်အစုံကို ဤနေရာတွင် ရှာဖွေနိုင်ပါသည်။

အပိုဆု- skewness နှင့် kurtosis ဂဏန်းတွက်စက်

ပေးထားသည့်ဒေတာအတွဲအတွက် skewness နှင့် kurtosis အလိုအလျောက်တွက်ချက်ပေးသော Statistical Skewness and Kurtosis Calculator ကို အသုံးပြု၍ ပေးထားသည့်ဒေတာအတွဲအတွက် sewness ကိုလည်း တွက်ချက်နိုင်သည် ။