Bayes' သီအိုရီ
ဤဆောင်းပါးတွင် Bayes’ theorem သည် အဘယ်အရာဖြစ်ပြီး ဖြစ်နိုင်ခြေနှင့် စာရင်းဇယားများတွင် အသုံးပြုထားသည်ကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ Bayes သီအိုရီ၏ ဖော်မြူလာမှာ အဘယ်နည်း၊ Bayes သီအိုရီ၏ နမူနာများကို ဖြေရှင်းပြီး ဤသီအိုရီ၏ အသုံးချပုံများကို သင်ရှာဖွေတွေ့ရှိမည်ဖြစ်သည်။
Bayes ရဲ့ သီအိုရီဆိုတာ ဘာလဲ။
ဖြစ်နိုင်ခြေသီအိုရီတွင်၊ Bayes’ theorem သည် ထိုအဖြစ်အပျက်နှင့်ပတ်သက်သော ဦးစားပေးအချက်အလက်များကို သိသောအခါ ဖြစ်ရပ်တစ်ခု၏ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အသုံးပြုသည့် ဥပဒေတစ်ခုဖြစ်သည်။
ပို၍တိကျသည်မှာ၊ Bayes ၏ သီအိုရီသည် သင်္ချာအားဖြင့် အဖြစ်အပျက် A ပေးထားသည့် အဖြစ်အပျက် B ၏ ဖြစ်နိုင်ခြေကို B ပေးထားသော A ၏ ဖြစ်နိုင်ခြေနှင့် ဆက်စပ်နေသည်။
ဥပမာအားဖြင့်၊ လူတစ်ဦးသည် တုပ်ကွေးမိပါက ခေါင်းကိုက်မည့် ဖြစ်နိုင်ခြေကို ကြိုတင်သိပါက၊ လူတစ်ဦးသည် ခေါင်းကိုက်သည့်အခါ တုပ်ကွေးဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် Bayes’ theorem ကို အသုံးပြုနိုင်သည်။
Bayes ၏သီအိုရီတွင် အသုံးချပရိုဂရမ်များစွာပါရှိပါသည်၊ ဥပမာအားဖြင့်၊ ၎င်းကို ဆေးပညာ၊ ဘောဂဗေဒ သို့မဟုတ် နည်းပညာတွင် အခြားဖြစ်ရပ်များက သတ်မှတ်ပေးထားသော အချို့သောဖြစ်ရပ်များ၏ ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန် အသုံးပြုပါသည်။ အောက်တွင်၊ Bayes’ theorem ၏ မတူညီသောအသုံးချမှုများအကြောင်း အသေးစိတ်ဖော်ပြပါမည်။
Bayes ၏သီအိုရီကို အင်္ဂလိပ်သင်္ချာပညာရှင် Thomas Bayes (1702-1761) မှ တီထွင်ခဲ့သည်၊
Bayes သီအိုရီ၏ဖော်မြူလာ
Bayes ၏ သီအိုရီက တူညီသော သီးသန့်ဖြစ်ရပ်များ {A 1 , A 2 ,…, A i ,…, A n } ၏ ဖြစ်နိုင်ခြေများသည် သုညမဟုတ်သော အခြားဖြစ်ရပ်တစ်ခု B ကို သင်္ချာနည်းဖြင့် ဆက်စပ်နိုင်သည်ဟု Bayes’ theorem ကဆိုသည်။ A ၏ဖြစ်နိုင်ခြေသည် A i ပေးထားသော B ၏အခြေအနေအရဖြစ်နိုင်ခြေနှင့် event B ကို ပေးသည်။
ထို့ကြောင့် Bayes ၏ သီအိုရီအတွက် ဖော်မြူလာမှာ Bayes’ rule ဟုလည်း ခေါ်သည် ၊

ရွှေ-
-
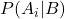
အဖြစ်အပျက် A နှင့် အဖြစ်အပျက် B ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေကို ၊ posterior probability ဟုခေါ်သည်။
-

အဖြစ်အပျက် B သည် ပေးထားသော အဖြစ်အပျက် A i ၏ အခြေအနေအရ ဖြစ်နိုင်ခြေ ဖြစ်သည် ။
-

ကြိုတင်ဖြစ်နိုင်ခြေဟုခေါ်သော A i သည် အဖြစ်အပျက်ဖြစ်နိုင်ခြေဖြစ်သည်။
Bayes ၏ သီအိုရီဖော်မြူလာ၏ ပိုင်းခြေသည် ဖြစ်ရပ် B ၏ စုစုပေါင်းဖြစ်နိုင်ခြေကို သတိပြုပါ။
Bayes သီအိုရီ၏ ဥပမာ
Bayes Theorem ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် မည်ကဲ့သို့ဖြစ်သည်ကို ကျွန်ုပ်တို့မြင်သည်နှင့်၊ သဘောတရားကို ပိုမိုနားလည်ရန် Bayes Theorem ဖြင့် ဖြစ်နိုင်ခြေကို တွက်ချက်ပုံ၏ ဖြေရှင်းပုံဥပမာတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။
- အီလက်ထရွန်နစ်ပစ္စည်းဆိုင်တစ်ခုတွင် တီဗီတံဆိပ်သုံးမျိုးရောင်းချသည်- X၊ Y၊ Z။ ရောင်းချမှု၏ 20% သည် အမှတ်တံဆိပ်၏ရုပ်မြင်သံကြားများ ချို့ယွင်းနေပြီး အမှတ်တံဆိပ် Y တီဗီများ၏ 3% မှာ ချွတ်ယွင်းနေပြီး Z အမှတ်တံဆိပ် တီဗီများ၏ 4% မှာ ချို့ယွင်းချက်ရှိသည်ဟု ခန့်မှန်းရသည်။ ချို့ယွင်းနေသောတီဗီတစ်ခုအား ပေးထားသော၊ ၎င်းသည် Brand Z TV ဖြစ်နိုင်ခြေအဘယ်နည်း။
လေ့ကျင့်ခန်းသည် သုံးစွဲသူတစ်ဦးသည် ရုပ်မြင်သံကြားအမှတ်တံဆိပ်တစ်ခုစီကို ဝယ်ယူမည့် ဖြစ်နိုင်ခြေများကို ပေးသည်-
- ပွဲ A 1 : ဝယ်ယူသူသည် အမှတ်တံဆိပ် X ရုပ်မြင်သံကြား → P(A 1 ) = 0.20 ဝယ်ယူသည်
- ပွဲ A 2 : ဝယ်ယူသူသည် Y အမှတ်တံဆိပ် တီဗီတစ်လုံးကို ဝယ်ယူသည် → P(A 2 ) = 0.50
- ပွဲ A 3 − ဝယ်ယူသူတစ်ဦးသည် Z အမှတ်တံဆိပ် ရုပ်မြင်သံကြား → P(A 3 ) = 0.30 ဝယ်ယူသည်
ထို့အပြင်၊ စာဖတ်ခြင်းသည် အမှတ်တံဆိပ်တစ်ခုစီ၏ ရုပ်မြင်သံကြားတစ်ခု၏ ချို့ယွင်းချက်ဖြစ်နိုင်ချေကိုလည်း ပေးသည်-
Event B- တီဗီက ပျက်နေတယ်။
- B|A 1 : အမှတ်တံဆိပ် X ရုပ်မြင်သံကြားကို ပေးထားသည့် ရုပ်မြင်သံကြားသည် ချွတ်ယွင်းနေသည် → P(B|A 1 )=0.05
- B|A 2 − အမှတ်တံဆိပ် Y ရုပ်မြင်သံကြားအား ပေးအပ်ထားသော ရုပ်မြင်သံကြားသည် ချို့ယွင်းချက် → P(B|A 2 )=0.03
- B|A 3 − အမှတ်တံဆိပ် Z ရုပ်မြင်သံကြားအား ပေးအပ်ထားသော ရုပ်မြင်သံကြားသည် ချို့ယွင်းချက် → P(B|A 3 )=0.04
ထို့ကြောင့် ကျွန်ုပ်တို့စိတ်ဝင်စားသည့် အဖြစ်အပျက်အားလုံး၏ ဖြစ်နိုင်ခြေသစ်ပင်မှာ အောက်ပါအတိုင်းဖြစ်သည်။

ထို့ကြောင့်၊ ချို့ယွင်းနေသော ရုပ်မြင်သံကြားကို ပေးထားသည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ရန်၊ ၎င်းသည် Z တံဆိပ်ဖြစ်သည်၊ ကျွန်ုပ်တို့သည် Bayes သီအိုရီမှ ဖော်မြူလာကို အသုံးပြုရပါမည်-

ဤဥပမာတွင်အသုံးပြုထားသောဝေါဟာရကိုအသုံးပြုခြင်းဖြင့် Bayes ၏ဖော်မြူလာသည်ဤကဲ့သို့ဖြစ်သည်-
![]()
ထို့ကြောင့်၊ ပေးထားသော ချွတ်ယွင်းနေသော ရုပ်မြင်သံကြားသည် အမှတ်တံဆိပ် Z ဖြစ်နိုင်ခြေကို တွက်ချက်ရာတွင် အောက်ပါအတိုင်းဖြစ်သည်။
![Rendered by QuickLaTeX.com \begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,04\cdot 0,30}{0,05\cdot 0,20+0,03\cdot 0,50+0,04\cdot 0,30}\\[2ex]&=0,32\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-818d0f3336f855a1315d6a94f01d1876_l3.png)
နိဂုံးချုပ်အားဖြင့်၊ ရုပ်မြင်သံကြား ချို့ယွင်းပါက၊ ၎င်းသည် အမှတ်တံဆိပ် Z ၏ ဖြစ်နိုင်ခြေ ၃၂% ဖြစ်သည်။
Bayes’ သီအိုရီ၏အသုံးချမှုများ
Bayes ၏ သီအိုရီ၏ အသုံးချမှုများစွာ အပါအဝင်၊
- ဆေးဘက်ဆိုင်ရာစစ်ဆေးမှုများ : Bayes ‘သီအိုရီကို ဆေးပညာတွင် မကြာခဏအသုံးပြုပြီး ရောဂါရှာဖွေစစ်ဆေးမှုများ အောင်မြင်ခြင်း၏ ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန်။ ဥပမာအားဖြင့်၊ HIV စမ်းသပ်မှုတစ်ခုတွင်၊ စမ်းသပ်မှုရလဒ်သည် အပေါင်းလက္ခဏာဖြစ်ပါက လူတစ်ဦးတွင် ဗိုင်းရပ်စ် အမှန်တကယ်ရှိနိုင်ခြေကို တွက်ချက်ရန် သီအိုရီကို အသုံးပြုနိုင်သည်။
- ငွေကြေးဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာခြင်း – ဘဏ္ဍာရေးတွင်၊ ဘိုင်ယန်သီအိုရီကို စီးပွားရေးကိန်းရှင်အစုတစ်ခုမှ ပေးဆောင်သည့် စတော့တန်ဖိုး တိုးခြင်း သို့မဟုတ် ကျဆင်းခြင်းကဲ့သို့သော စီးပွားရေးဆိုင်ရာ ဖြစ်ရပ်အချို့ ဖြစ်ပေါ်လာနိုင်ခြေကို တွက်ချက်ရန်အတွက် Bayes’ theorem ကို အသုံးပြုပါသည်။
- စျေးကွက်သုတေသန : Bayes’ theorem သည် ဥပမာအားဖြင့်၊ ဤထုတ်ကုန်အတွက် ကြော်ငြာတစ်ခုမြင်ပြီးနောက် လူတစ်ဦးသည် ကုန်ပစ္စည်းတစ်ခုဝယ်ယူမည့်ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန်ဖြစ်နိုင်ချေရှိသည်။
- မိုးလေဝသခန့်မှန်းခြင်း – လေ့လာတွေ့ရှိထားသောဒေတာအပေါ်အခြေခံ၍ ပေးထားသည့် မိုးလေဝသခန့်မှန်းချက်သည် ဖြစ်နိုင်ခြေကိုဆုံးဖြတ်ရန် မိုးလေဝသမော်ဒယ်များသည် Bayes ၏သီအိုရီကိုအသုံးပြုသည်။ ၎င်းသည် ရာသီဥတုခန့်မှန်းချက်များ၏ တိကျမှုကို တိုးတက်စေသည်။
- ကွန်ပြူတာလုံခြုံရေး – ဆိုက်ဘာလုံခြုံရေးတွင် သံသယဖြစ်ဖွယ်လုပ်ဆောင်ချက်သည် ကွန်ပျူတာစနစ်အပေါ် အမှန်တကယ်တိုက်ခိုက်မှုဖြစ်နိုင်ချေကို ဆုံးဖြတ်ရန် Bayes သီအိုရီကို အသုံးချနိုင်သည်။
Bayes သီအိုရီပြဿနာများကို ဖြေရှင်းထားသည်။
လေ့ကျင့်ခန်း ၁
လူဦးရေ၏ ၁ ရာခိုင်နှုန်းသည် အချို့သော ရောဂါဝေဒနာများကို ခံစားနေရသည်ဟု ခန့်မှန်းရသည်။ ဤရောဂါကိုသိရှိရန် စမ်းသပ်မှုတစ်ခုသည် အပြုသဘောဆောင်သောရောဂါများအတွက် 95% တိကျပြီး 90% သည် အနုတ်လက္ခဏာဆောင်သောရောဂါများအတွက် တိကျပါသည်။ ကျပန်းရွေးချယ်ထားသောလူတစ်ဦးသည် အပြုသဘောဆောင်ပါက၊ ၎င်းတို့တွင် အမှန်တကယ်ရောဂါရှိနိုင်ခြေ မည်မျှရှိသနည်း။
လေ့ကျင့်ခန်းထုတ်ပြန်ချက်သည် ကျွန်ုပ်တို့အား အောက်ပါ ဖြစ်နိုင်ခြေများကို ပေးသည်-
A 1 : လူတွင် ရောဂါ → P(A 1 ) = 0.01
A 2 : လူတွင် ရောဂါမရှိပါ → P(A 2 ) = 0.99
B: စာမေးပွဲက positive ပါ။
B|A 1 : လူတွင် ရောဂါရှိသောအခါ စမ်းသပ်မှုမှာ positive → P(B|A 1 )=0.95၊
B|A 2 : လူတွင် ရောဂါမရှိသောအခါ စစ်ဆေးမှုသည် positive → P(B|A 2 )=1-0.90=0.10
ထို့နောက်၊ ကျပန်းရွေးချယ်ထားသောလူတစ်ဦးတွင် အပြုသဘောဆောင်သောစမ်းသပ်မှုတွင် ရောဂါ အမှန်တကယ်ရှိနိုင်ခြေကို တွက်ချက်ရန်၊ Bayes ၏ စည်းမျဉ်းကို ကျင့်သုံးရမည်-

![]()
ထို့ကြောင့် ကျွန်ုပ်တို့သည် တန်ဖိုးများကို ဖော်မြူလာတွင် အစားထိုးပြီး ဖြစ်နိုင်ခြေ တွက်ချက်မှုကို လုပ်ဆောင်သည်-
![Rendered by QuickLaTeX.com \begin{aligned}P(A_1|B)&=\cfrac{P(B|A_1)\cdot P(A_1)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)}\\[2ex]&=\cfrac{0,95\cdot 0,01}{0,95\cdot 0,01+0,10\cdot 0,99}\\[2ex]&=0,0876\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-135e9ab7de6b44e7392fae0f5e70a125_l3.png)
အတိုချုပ်ပြောရလျှင် ကျပန်းရွေးချယ်ထားသောလူသည် အပေါင်းလက္ခဏာဆောင်ပြီး အမှန်တကယ် ရောဂါရှိနေသော ဖြစ်နိုင်ခြေမှာ 8.76% ဖြစ်သည်။
လေ့ကျင့်ခန်း ၂
တစ်နေ့တွင် စတော့ရှယ်ယာတစ်ခု တက်လာနိုင်သည့် ဖြစ်နိုင်ခြေမှာ 40% ဖြစ်ပြီး ၎င်းသည် တည်ငြိမ်နေမည်ဖြစ်ပြီး 10% နှင့် ၎င်းသည် 50% ကျဆင်းမည်ဟု ခန့်မှန်းထားသည်။ ထို့အပြင်၊ စျေးကွက်တက်လာသောအခါ၊ ငွေကြေးလေ့လာသုံးသပ်သူသည် မှန်ကန်စွာခန့်မှန်းနိုင်ခြေ 90% ရှိကြောင်း၊ စျေးကွက်တည်ငြိမ်နေသည့်အခါ ခန့်မှန်းချက်မှန်ကန်မည့် ဖြစ်နိုင်ခြေမှာ 75% ဖြစ်ပြီး ကျဆင်းသွားပါက၊ မှန်ကန်သော ခန့်မှန်းချက်တစ်ခု၏ ဖြစ်နိုင်ခြေသည် 75% ဖြစ်သည်။ ၈၅%%။ စျေးကွက်ကျဆင်းမည်ဟု ကျွမ်းကျင်သူတစ်ဦးက ခန့်မှန်းပါက၊ အမှန်တကယ် ကျဆင်းနိုင်ခြေ မည်မျှရှိသနည်း။
ဤကိစ္စတွင်၊ လေ့ကျင့်ခန်းထုတ်ပြန်ချက်သည် ကျွန်ုပ်တို့အား အောက်ပါဖြစ်နိုင်ခြေများကို ပေးသည်-
A 1 : တစ်ရက်အတွင်း စျေးကွက်တက်လာသည် → P(A 1 ) = 0.40
A 2 : စျေးကွက်သည် တစ်ရက်အတွင်း တည်ငြိမ်နေဆဲ → P(A 2 ) = 0.10
A 3 : တစ်ရက်အတွင်း စျေးကွက်တက်လာသည် → P(A 3 ) = 0.50
B : စျေးကွက်က ကျဆင်းမယ်လို့ ခန့်မှန်းတယ်။
B|A 1 : စျေးကွက်တိုးလာမည်ဟု မှန်ကန်စွာ ခန့်မှန်းသည် → P(B|A 1 )=0.90
B|A 2 : စျေးကွက်တည်ငြိမ်နေဆဲဖြစ်ကြောင်း ဆန်းစစ်သူမှ မှန်ကန်စွာ ခန့်မှန်းသည် → P(B|A 2 )=0.75
B|A 3 : စျေးကွက်ကျဆင်းမည်ဟု ဆန်းစစ်သူ မှန်ကန်စွာ ခန့်မှန်းသည် → P(B|A 3 )=0.85
စျေးကွက်ကျဆုံးမည့် ခန့်မှန်းချက်မှန်ကန်ကြောင်း သုံးသပ်သူမှ ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန်အတွက် Bayes Theorem ဖော်မြူလာကို အသုံးပြုရန် လိုအပ်သည်-

![]()
ကျွန်ုပ်တို့သည် ဖြစ်နိုင်ခြေတန်ဖိုးများကို Bayes ဖော်မြူလာဖြင့် အစားထိုးပြီး ဖြစ်နိုင်ခြေကို တွက်ချက်သည်-
![Rendered by QuickLaTeX.com \begin{aligned}P(A_3|B)&=\cfrac{P(B|A_3)\cdot P(A_3)}{P(B|A_1)\cdot P(A_1)+P(B|A_2)\cdot P(A_2)+ P(B|A_3)\cdot P(A_3)}\\[2ex]&=\cfrac{0,85\cdot 0,50}{0,90\cdot 0,40+0,75\cdot 0,10+0,85\cdot 0,50}\\[2ex]&=0,4942\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9f98a5a8a91299aa55aab02159dcebec_l3.png)
ထို့ကြောင့်၊ စတော့ရှယ်ယာဈေးကွက် ကျဆင်းမည်ဟု သုတေသီတစ်ဦးမှ ပြောသောအခါ မှန်ကန်သောဖြစ်နိုင်ခြေမှာ 49.42% ဖြစ်သည်။