Benford ၏ဥပဒေ
ဤဆောင်းပါးတွင် Benford ၏ဥပဒေသည် မည်သည်ကို ရှင်းပြထားသည်။ ထို့အပြင်၊ Benford ၏ဥပဒေအား မည်သို့ရှာဖွေတွေ့ရှိပြီး ဤစာရင်းအင်းဥပဒေ၏အသုံးချမှုများကို သင်တွေ့မြင်နိုင်မည်ဖြစ်ပါသည်။
Benford ၏ဥပဒေဆိုတာဘာလဲ။
Benford’s law ၊ the law of the first digit ဟုလည်း ခေါ်သည် ၊ သည် အချက်အလက် အပိုင်းအစ ၏ ပထမ ဂဏန်း သည် 1 ဖြစ်နိုင်ခြေ သည် အခြား ကိန်း များ ထက် ဖြစ်နိုင်ခြေ ပိုများ သည်ဟု ကိန်းဂဏန်း ဆိုင်ရာ ဥပဒေ တစ်ရပ် ဖြစ်သည် ။
တစ်နည်းဆိုရသော် Benford ၏ ဥပဒေက လက်တွေ့ဘဝတွင် တည်ရှိနေသော ကိန်းဂဏာန်းဒေတာအစုတစ်ခုတွင် နံပါတ် 1 သည် ဒေတာ၏ပထမဂဏန်းအဖြစ် ထပ်ခါထပ်ခါဖြစ်နေသော ဂဏန်းဖြစ်သည်ဟု ဆိုသည်။
ထို့အပြင် အရေအတွက်များလေ၊ ပထမနေရာတွင် ရပ်တည်ရန် အလားအလာနည်းလေဖြစ်သည်။ ထို့ကြောင့် ပထမဂဏန်းသည် 1 ထက် 2 ဖြစ်နိုင်ချေ ပိုများသော်လည်း 2 သည် 3 ထက် ပိုများသည်၊ 3 သည် 4 ထက် ပိုများသည်။
Benford ၏ဥပဒေသည်အမေရိကန် Frank Benford မှ၎င်း၏အမည်ကိုပေးဆောင်သည်။ ၎င်းကို မတီထွင်ခဲ့သော်လည်း Benford သည် ဤစာရင်းအင်းစည်းမျဉ်းကို လူကြိုက်များခဲ့သည်။ အောက်တွင် Benford ၏ဥပဒေ၏ဇာစ်မြစ်ကိုတွေ့ရပါမည်။
Benford ၏ဥပဒေဖော်မြူလာ
Benford ၏ဥပဒေတွင် ပထမဂဏန်းသည် အချို့သောဂဏန်းများ၏ဖြစ်နိုင်ခြေသည် ထိုဂဏန်းများထက်တစ်ပေါင်း၏ လော့ဂရစ်သမ်နှင့် ညီမျှသည်ဟု ဖော်ပြထားသည်။
ထို့ကြောင့် Benford ၏ဥပဒေအတွက် ပုံသေနည်းမှာ အောက်ပါအတိုင်းဖြစ်သည်။
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle P[X=d]=\log_{10}\left(1+\frac{1}{d}\right)\\[4ex]d=1,2,3,\ldots ,9\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a77defb5b209293a074ac2bee02c2e07_l3.png)
ထို့ကြောင့်၊ Benford ၏ ဥပဒေဖော်မြူလာမှ၊ ၎င်းသည် ဒေတာပစ္စည်းတစ်ခု၏ ပထမဂဏန်းဖြစ်သည်ဟူသော နံပါတ်တစ်ခုစီအတွက် ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ ရယူနိုင်ပါသည်။ အောက်ပါဇယားတွင် ဖြစ်နိုင်ခြေအားလုံး၏ ရာခိုင်နှုန်းများကို သင်တွေ့နိုင်သည်-
| ပုံ | ဖြစ်နိုင်ချေ များပါတယ်။ ပထမနံပါတ်ဖြစ်ပါစေ။ |
|---|---|
| ၁ | 30.1% |
| ၂ | 17.6% |
| ၃ | 12.5% |
| ၄ | ၉.၇% |
| ၅ | 7.9% |
| ၆ | 6.7% |
| ၇ | ၅.၈% |
| ၈ | 5.1% |
| ၉ | 4.6% |
ထို့အပြင်၊ အောက်တွင် Benford ၏ ဥပဒေဖြစ်နိုင်ခြေအားလုံးကို ဂရပ်ဖစ်ဖြင့် ကိုယ်စားပြုထားသည့် histogram ကို သင်တွေ့နိုင်သည်-
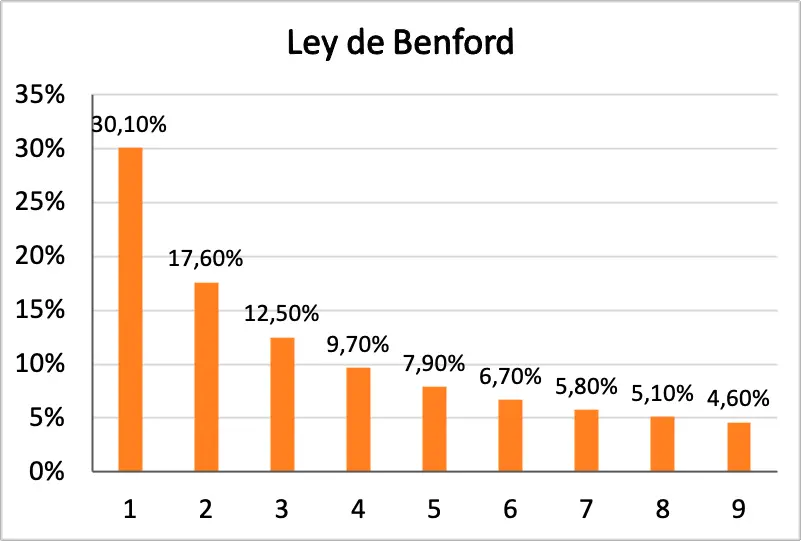
Benford ၏ဥပဒေသမိုင်း
1881 တွင် သင်္ချာပညာရှင် Simon Newcomb သည် လော့ဂရစ်သမ်ဇယားများ၏ ပထမစာမျက်နှာများကို နောက်ဆုံးစာမျက်နှာများထက် များစွာပိုမိုအသုံးပြုကြောင်း တွေ့ရှိသောအခါ Benford ၏ဥပဒေအား နုတ်ထွက်ခဲ့သည်။ ဆိုလိုသည်မှာ ဂဏန်းများ၏ ပထမဂဏန်းများသည် တန်းတူရည်တူ ဖြစ်နိုင်ချေ မရှိသော်လည်း 1 သည် 2 ထက် မကြာခဏ ၊ 2 ထက် ပိုမကြာခဏ 3 နှင့် 9 အထိ စသည်တို့ဖြစ်သည်။
သို့သော်လည်း Newcomb သည် ဤစည်းမျဉ်းကို လိုက်နာကြောင်း ကိန်းဂဏန်း အထောက်အထားများ မထားခဲ့ဘဲ၊ သူသည် လော့ဂရစ်သမ် ဇယားများ၏ စုတ်ပြဲခြင်းမှ နုတ်ထွက်ခဲ့သည်။
အထူးသဖြင့် 1938 ခုနှစ် နောက်ပိုင်းတွင် ရူပဗေဒပညာရှင် Frank Benford သည် အလားတူ စူးစမ်းလေ့လာမှုကို ပြုလုပ်ခဲ့ပြီး လက်တွေ့ကျကျ စစ်ဆေးရန် စမ်းသပ်မှုတစ်ခုကိုလည်း ပြုလုပ်ခဲ့သည်။ မတူညီသောနမူနာ 20 ခုမှ တန်ဖိုး 20,229 ၏ ကိန်းဂဏန်း အချက်အလက်အစုံတွင် ဒေတာတစ်ခုစီ၏ ပထမဂဏန်းကို လေ့လာခဲ့သည်။ ထို့ကြောင့်၊ ရလဒ်များအပေါ်အခြေခံ၍ Benford ၏ဥပဒေသည် ပြည့်စုံပြီး ပထမဂဏန်း၏ဖြစ်နိုင်ခြေကို တွက်ချက်နိုင်စေသည့်ဖော်မြူလာကို နုတ်ယူခဲ့ကြောင်း သရုပ်ပြခဲ့သည် (အထက်တွင် ဤပုံသေနည်းကို ကျွန်ုပ်တို့တွေ့ခဲ့ရသည်)။
အတိုချုပ်ပြောရလျှင် Benford’s Law ကို Simon Newcomb မှ ပထမဆုံးရှာဖွေတွေ့ရှိခဲ့သော်လည်း၊ သူသည် ဤစာရင်းအင်းဥပဒေအား အတည်ပြုသူဖြစ်သောကြောင့် Frank Benford ၏အမည်ကို ခေါ်ဆိုခြင်းဖြစ်သည်။
Benford ၏ဥပဒေအသုံးချမှုများ
Benford ၏ဥပဒေသည် အလွန်ကွဲပြားသောနယ်ပယ်များတွင် application များကိုရှာဖွေနိုင်သော ကိန်းဂဏန်းဥပဒေတစ်ခုဖြစ်သည်။ ဥပမာအားဖြင့်၊ Benford ၏ဥပဒေသည် စီးပွားရေး၊ ဇီဝဗေဒနှင့် နိုင်ငံရေးတွင်ပင် တွင်ကျယ်စွာအသုံးပြုသည်။
ဘောဂဗေဒတွင် Benford ၏ဥပဒေသည် ဒေတာကို ခြယ်လှယ်ခြင်းအား သိရှိရန် မကြာခဏအသုံးပြုသည်၊ အကြောင်းမှာ ဒေတာအစုံသည် Benford ၏ဥပဒေနှင့် မကိုက်ညီပါက၊ ဒေတာကို ခြယ်လှယ်ထားကြောင်း ညွှန်ပြသောကြောင့်ဖြစ်သည်။ ဥပမာအားဖြင့်၊ ဤဥပဒေသည် အခွန်လိမ်လည်မှုဖြစ်နိုင်ချေများကို ရှာဖွေဖော်ထုတ်ရန် အသုံးပြုသည်။
ရလဒ်များသည် တူညီနိုင်သောကြောင့် Benford ၏ ဥပဒေသည် ကျပန်းဖြစ်စဉ်များ၏ အမှန်တရားကို သရုပ်ပြရန် အသုံးမပြုကြောင်း သတိပြုသင့်သည်။ ထို့ကြောင့် Benford ၏ စည်းမျဉ်းကို ထီရလဒ်များကို အတည်ပြုရန် အသုံးပြု၍မရပါ။
အခြားတစ်ဖက်တွင်၊ မျိုးရိုးဗီဇတွင် Benford ၏ဥပဒေသည် မတူညီသောသက်ရှိအမျိုးအစားများကြားတွင် မျိုးရိုးဗီဇအရှည်ကွဲပြားမှုကို ခွဲခြမ်းစိတ်ဖြာရန် အသုံးပြုနိုင်သည်။
နောက်ဆုံးတွင်၊ ဤကိစ္စတွင် ၎င်း၏အသုံးဝင်မှုကို မေးခွန်းထုတ်သော်လည်း Benford ၏ဥပဒေအားကျင့်သုံးခြင်းဖြင့် မဲဆန္ဒရှင်မသမာမှုများကိုရှာဖွေရန် ကြိုးပမ်းမှုများပြုလုပ်ခဲ့သည်။