Benjamini-hochberg လုပ်ထုံးလုပ်နည်းလမ်းညွှန်

သင်သည် ကိန်းဂဏန်းစမ်းသပ်မှုတစ်ခုကို ပြုလုပ်သည့်အခါတိုင်း၊ သင်၏ null အယူအဆသည် မှန်နေသော်လည်း၊ သင်သည် p-value ထက် 0.05 ထက်နည်းသော အခွင့်အလမ်းကို ရရှိမည်ဖြစ်သည်။

ဥပမာအားဖြင့်၊ အပင်တစ်ပင်သည် ပျမ်းမျှအမြင့် 10 လက်မထက် ပိုကြီးသလား သိချင်သည်ဆိုကြပါစို့။ စမ်းသပ်ခြင်းအတွက် သင်၏ null နှင့် အခြားအခြားသော ယူဆချက်များသည်-

H ₀ : μ = 10 လက်မ

H _A : μ > 10 လက်မ

ဤယူဆချက်ကို စမ်းသပ်ရန်အတွက် သင်သည် အပြင်ထွက်၍ တိုင်းတာရန် အပင် 20 ၏ ကျပန်းနမူနာကို ကောက်ယူနိုင်သည်။ ဤအပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်သည် 10 လက်မဖြစ်သော်လည်း၊ သင်သည် ပုံမှန်မဟုတ်သောအရပ်ရှည်သည့်အပင် 20 ၏နမူနာကိုရွေးချယ်ပြီး null hypothesis ကိုငြင်းပယ်ရန်သင့်အားဖြစ်စေသည်။

(ဤအပင်၏ပျမ်းမျှအမြင့်မှာအမှန်တကယ် 10 လက်မဖြစ်သည်) ပျက်ပြယ်သောယူဆချက်သည်မှန်လျှင်ပင် သင်သည် ၎င်းကိုငြင်းပယ်ခဲ့သည်။ စာရင်းဇယားအရ၊ ဒါကို “ မှားယွင်းသောရှာဖွေတွေ့ရှိမှု” လို့ခေါ်ပါတယ်။ ရှာဖွေတွေ့ရှိမှုတစ်ခု – “ သိသာထင်ရှားသောရလဒ်” ကို သင်ပြုလုပ်ခဲ့သည်ဟု ဆိုသော်လည်း၊ ၎င်းသည် အမှန်တကယ် မှားယွင်းပါသည်။

ယခု ကိန်းဂဏန်း စစ်ဆေးမှု 100 ကို တစ်ပြိုင်နက် လုပ်ဆောင်ရန် စိတ်ကူးကြည့်ပါ။ 0.05 ရှိသော alpha အဆင့်ကို အသုံးပြု၍ တစ်ဦးချင်းစမ်းသပ်မှုတစ်ခုနှင့် မှားယွင်းသောရှာဖွေတွေ့ရှိရန် 5% အခွင့်အလမ်းသာရှိသော်လည်း၊ သင်သည်ထိုကဲ့သို့သောစမ်းသပ်မှုများစွာကိုပြုလုပ်သောကြောင့်၊ သင်သည် မှားယွင်းသောရှာဖွေတွေ့ရှိမှုဆီသို့ ဦးတည်သွားစေရန် 5% ခန့်သာမျှော်လင့်နိုင်မည်ဖြစ်သည်။

ခေတ်သစ်ကမ္ဘာကြီးတွင် သုတေသီများအား ကိန်းဂဏန်းစမ်းသပ်မှု ရာပေါင်းများစွာ သို့မဟုတ် ထောင်ပေါင်းများစွာကိုပင် တစ်ကြိမ်လျှင် နည်းပညာဖြင့် လုပ်ဆောင်နိုင်သောကြောင့် မှားယွင်းသောရှာဖွေတွေ့ရှိမှုများသည် အဖြစ်များသောပြဿနာတစ်ခုဖြစ်နိုင်သည်။

ဥပမာအားဖြင့်၊ ဆေးသုတေသီများသည် တစ်ကြိမ်လျှင် သောင်းနှင့်ချီသော မျိုးဗီဇများကို ကိန်းဂဏန်းစမ်းသပ်မှုများ ပြုလုပ်နိုင်သည်။ မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်းသည် 5% သာရှိသော်လည်း ရာနှင့်ချီသောစမ်းသပ်မှုများသည် မှားယွင်းသောရှာဖွေတွေ့ရှိမှုများဖြစ်ပေါ်နိုင်သည်ဟု ဆိုလိုသည်။

မှားယွင်းသော ရှာဖွေတွေ့ရှိမှုနှုန်းကို ထိန်းချုပ်ရန် နည်းလမ်းတစ်ခုမှာ Benjamini-Hochberg လုပ်ထုံးလုပ်နည်းကို အသုံးပြုခြင်းဖြစ်သည်။

Benjamini-Hochberg လုပ်ထုံးလုပ်နည်း

Benjamini-Hochberg လုပ်ထုံးလုပ်နည်းသည် အောက်ပါအတိုင်း လုပ်ဆောင်သည်။

အဆင့် 1- သင်၏စာရင်းအင်းစစ်ဆေးမှုအားလုံးကိုလုပ်ဆောင်ပြီး စမ်းသပ်မှုတစ်ခုစီအတွက် p-value ကိုရှာပါ။

အဆင့် 2- p-တန်ဖိုးများကို ကြီးစဉ်ငယ်လိုက် အဆင့်သတ်မှတ်ပြီး၊ တစ်ခုစီအတွက် အဆင့်သတ်မှတ်ခြင်း- အငယ်ဆုံးတန်ဖိုးသည် အဆင့် 1 ရှိပြီး နောက်အသေးဆုံးသည် အဆင့် 2 ရှိသည်၊ စသည်တို့ဖြစ်သည်။

အဆင့် 3- ဖော်မြူလာ (i/m)*Q ကို အသုံးပြု၍ p-value တစ်ခုစီအတွက် အရေးကြီးသော Benjamini-Hochberg တန်ဖိုးကို တွက်ချက်ပါ။

ရွှေ-

i = p တန်ဖိုးအဆင့်

m = စုစုပေါင်းစမ်းသပ်မှုအရေအတွက်

မေး = သင်ရွေးချယ်ထားသော မှားယွင်းသော ရှာဖွေတွေ့ရှိမှုနှုန်း

အဆင့် 4- အရေးကြီးသောတန်ဖိုးထက်နည်းသော အကြီးဆုံး p-တန်ဖိုးကို ရှာပါ။ ဤ p-တန်ဖိုးထက်နည်းသော p-တန်ဖိုးတစ်ခုစီကို သိသာထင်ရှားစွာ သတ်မှတ်ပါ။

အောက်ဖော်ပြပါ ဥပမာသည် ဤလုပ်ငန်းစဉ်ကို ခိုင်မာသောတန်ဖိုးများဖြင့် မည်သို့ဆောင်ရွက်ရမည်ကို ဖော်ပြသည်။

ဥပမာ

သုတေသီများသည် နှလုံးရောဂါနှင့် ပတ်သက်သည့် မတူညီသော ကိန်းရှင် 20 ကို ဆုံးဖြတ်လိုသည်ဆိုကြပါစို့။ ၎င်းတို့သည် တစ်ကြိမ်လျှင် စာရင်းအင်းစစ်ဆေးမှု 20 ကိုလုပ်ဆောင်ပြီး စာမေးပွဲတစ်ခုစီအတွက် p-value ကိုရရှိမည်ဖြစ်သည်။ အောက်ပါဇယားသည် စမ်းသပ်မှုတစ်ခုစီအတွက် p-တန်ဖိုးများကို ကြီးစဉ်ငယ်လိုက် ဖော်ပြထားပါသည်။

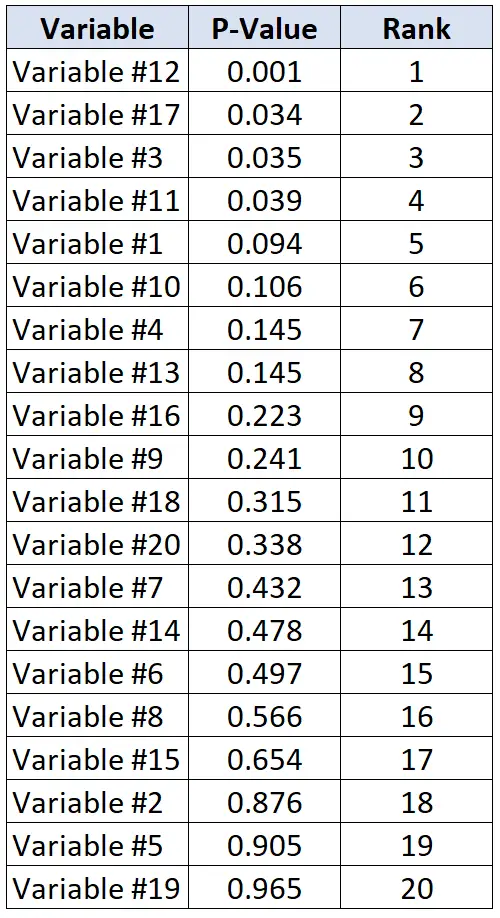
သုတေသီများသည် မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်း 20% ကို လက်ခံလိုသည်ဆိုပါစို့။ ထို့ကြောင့် p-value တစ်ခုစီအတွက် အရေးပါသော Benjamini-Hochberg တန်ဖိုးကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို သုံးနိုင်သည်- (i/20)*0.2 where i = p-value ၏ အဆင့်။

အောက်ပါဇယားတွင် p-value တစ်ခုစီအတွက် အရေးကြီးသော Benjamini-Hochberg တန်ဖိုးကို ပြသသည်-

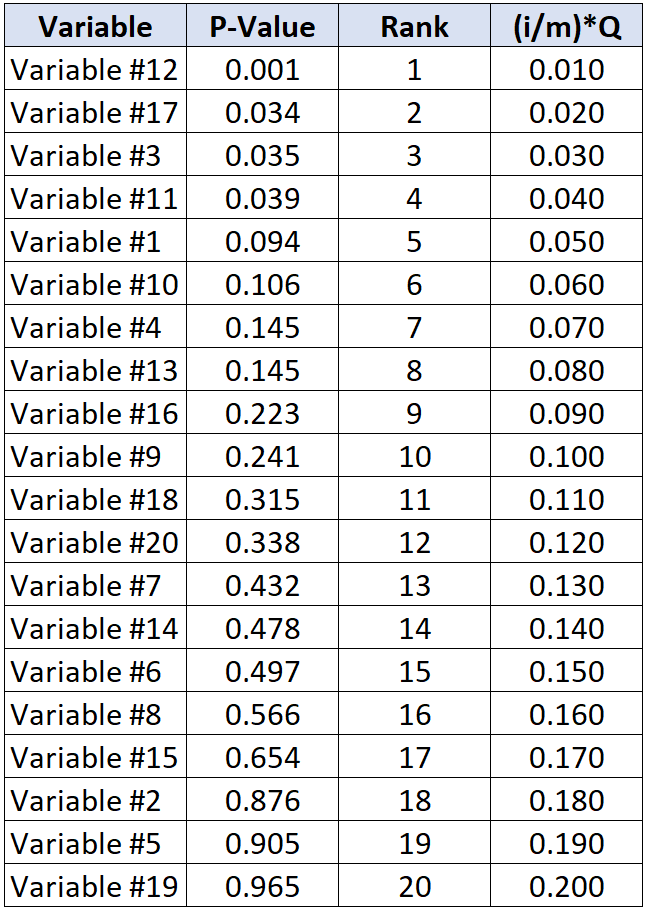
၎င်း၏ Benjamini-Hochberg အရေးကြီးသောတန်ဖိုးအောက်တွင် အကြီးဆုံး p-တန်ဖိုးရှိသော စမ်းသပ်မှုသည် p-တန်ဖိုး 0.039 နှင့် BH အရေးကြီးတန်ဖိုး 0.040 ရှိသည့် ကိန်းရှင် #11 ဖြစ်သည်။

ထို့ကြောင့်၊ ဤစမ်းသပ်မှုနှင့် p-value သေးသေးဖြင့် စမ်းသပ်မှုအားလုံးကို သိသာထင်ရှားစွာ မှတ်ယူမည်ဖြစ်သည်။

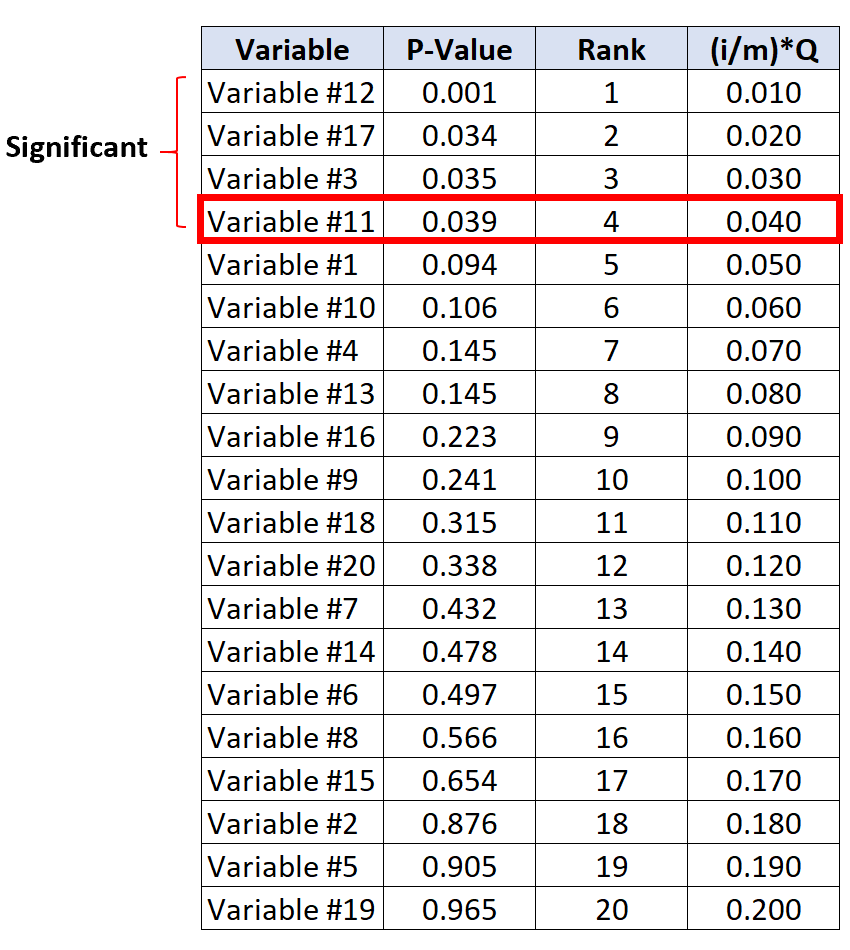
#17 နှင့် #3 တို့သည် variable #11 ထက် p-values များထက်သေးငယ်သော p-values များမရှိသော်လည်း၊ ၎င်းတို့တွင် p-values များထက် သေးငယ်သောကြောင့်၎င်းတို့သည် သိသာထင်ရှားသည်ဟု မှတ်ယူပါ။

မှားယွင်းသော ရှာဖွေတွေ့ရှိမှုနှုန်းကို ရွေးချယ်နည်း

Benjamini-Hochberg လုပ်ထုံးလုပ်နည်းတွင် အရေးကြီးဆုံးအဆင့်များထဲမှတစ်ခုမှာ မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်းကို ရွေးချယ်ခြင်းဖြစ်သည်။ ဒေတာမစုဆောင်းမီ သို့မဟုတ် စာရင်းအင်းစစ်ဆေးမှုများမလုပ်ဆောင်မီ သင်၏မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်းကို သင်ရွေးချယ်သင့်သည်။

ပုံမှန်အားဖြင့်၊ သင်သည် သင်၏ခွဲခြမ်းစိတ်ဖြာမှု၏ စူးစမ်းလေ့လာရေးအဆင့်တွင် ကိန်းဂဏန်းစမ်းသပ်မှုအများအပြားကို လုပ်ဆောင်ရမည်ဖြစ်ပြီး၊ ထို့နောက်တွင် သင်၏ရလဒ်များကို ပိုမိုစူးစမ်းလေ့လာရန် အခြားစမ်းသပ်မှုများနှင့်အတူ ဆက်လက်လုပ်ဆောင်မည်ဖြစ်သည်။

နောက်ဆက်တွဲစစ်ဆေးမှုသည် စျေးမကြီးပါက၊ သင့်တွင် မှားယွင်းသောရှာဖွေတွေ့ရှိမှုအနည်းငယ်ရှိသော်လည်း နောက်ဆက်တွဲစမ်းသပ်မှုတွင် အဆိုပါမှားယွင်းသောရှာဖွေတွေ့ရှိမှုအား သင်ရှာဖွေတွေ့ရှိနိုင်ဖွယ်ရှိသောကြောင့် မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်းကို သင်ပိုမိုမြင့်မားစွာသတ်မှတ်ရန် စဉ်းစားနိုင်ပါသည်။

ထို့အပြင်၊ အရေးကြီးသောရှာဖွေတွေ့ရှိမှုတစ်ခုပျောက်ဆုံးခြင်းအတွက် ကုန်ကျစရိတ်မြင့်မားပါက၊ အရေးကြီးသောအရာကို လက်လွတ်မခံစေရန် သင်၏မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်းကို တိုးမြှင့်လိုပေမည်။

သင်၏ သုတေသနကုန်ကျစရိတ်နှင့် အရေးကြီးသောတွေ့ရှိချက်များကို မပျက်မကွက်ပြုလုပ်ခြင်း၏ အရေးကြီးမှုအပေါ်မူတည်၍ မှားယွင်းသောရှာဖွေတွေ့ရှိမှုနှုန်းသည် အခြေအနေတစ်ခုနှင့်တစ်ခု ကွဲပြားမည်ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

P တန်ဖိုးများနှင့် စာရင်းအင်းဆိုင်ရာ အရေးပါမှုဆိုင်ရာ ရှင်းလင်းချက်
မိသားစုအလိုက် အမှားအယွင်းနှုန်းက ဘယ်လောက်လဲ။