Bernoulli ဖြန့်ဖြူးခြင်းနှင့် binomial ဖြန့်ဖြူးခြင်း- ကွာခြားချက်ကား အဘယ်နည်း။

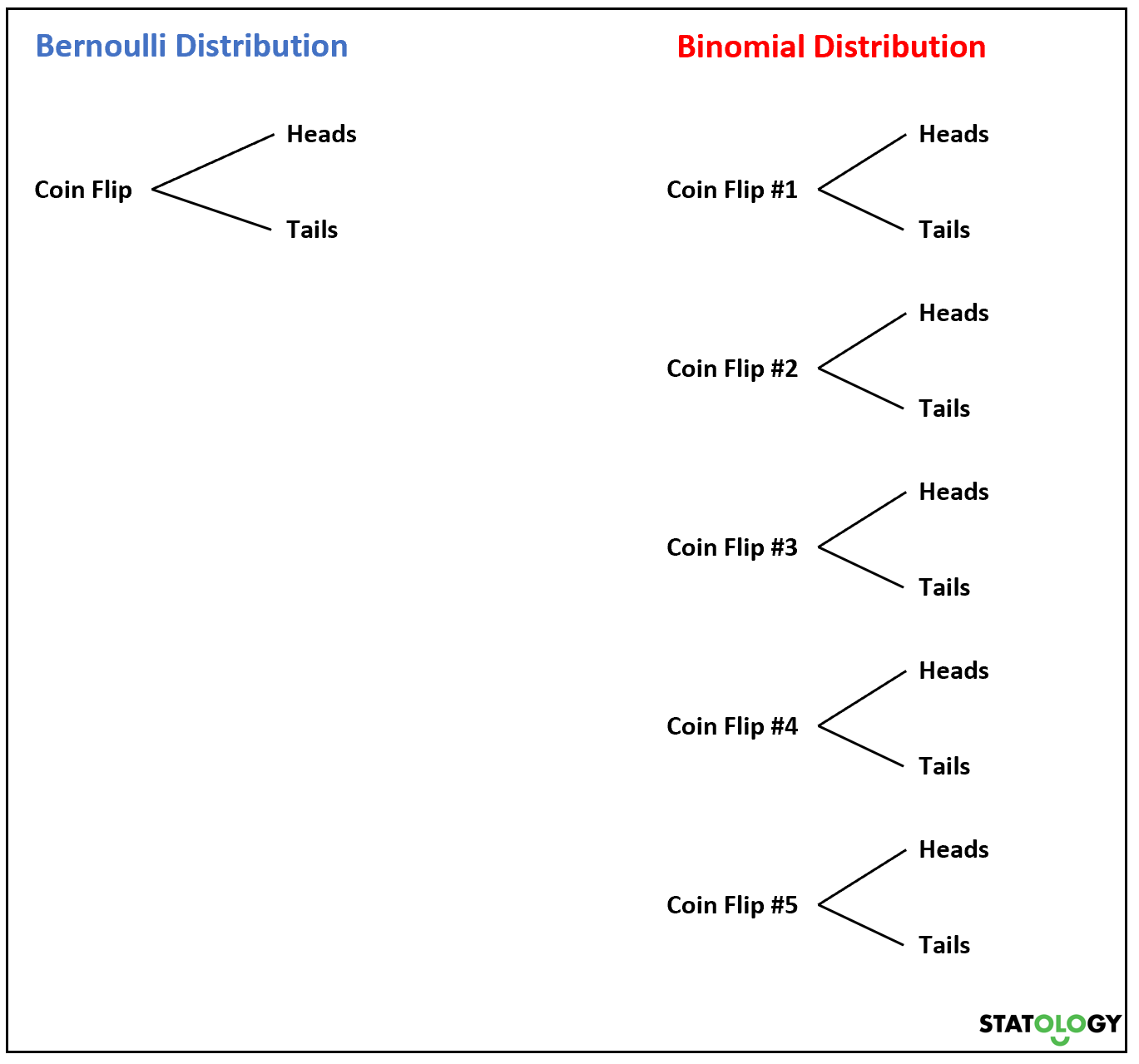
ဖြစ်နိုင်ချေ ရလဒ် နှစ်ခုသာ ရှိသည်- 0 သို့မဟုတ် 1 သာ ရှိပါက Bernoulli ဖြန့်ဖြူးမှုနောက်တွင် ကျပန်းပြောင်းလဲနိုင်သော ကိန်းရှင် တစ်ခု လိုက်နာပါ။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် အကြွေစေ့တစ်ခုကို တစ်ကြိမ်ပစ်သည်ဆိုပါစို့။ p ထားပါတော့။ ဆိုလိုသည်မှာ ၎င်းအမြီးများဆင်းသက်နိုင်ခြေမှာ 1- p ဖြစ်သည်။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့ရေးနိုင်သည်-

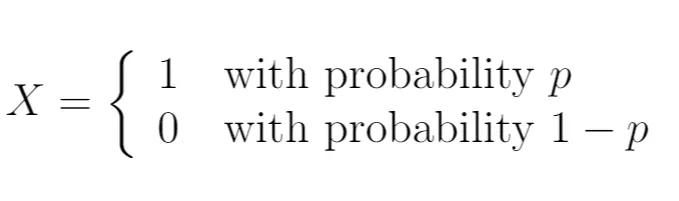
ဤကိစ္စတွင်၊ ကျပန်းပြောင်းလဲနိုင်သော X သည် Bernoulli ဖြန့်ဝေမှုကို လိုက်နာသည်။ ဖြစ်နိုင်ချေတန်ဖိုးနှစ်ခုသာ ယူနိုင်သည်။

ယခု၊ ကျွန်ုပ်တို့သည် အကြွေစေ့တစ်ခုကို အကြိမ်များစွာလှန်ပါက၊ Bernoulli ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင်များ၏ ပေါင်းလဒ်သည် binomial ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်လိမ့်မည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် အကြွေစေ့တစ်ခုကို 5 ကြိမ်ပစ်ချလိုက်ပြီး head k ကြိမ်ရနိုင်ခြေကို သိလိုသည်ဆိုပါစို့။ ကျပန်း ပြောင်းလဲနိုင်သောပုံစံဖြစ်သည်။

ကျပန်း variable X သည် binomial distribution ကို လိုက်နာပါက၊ X = k အောင်မြင်မှု ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ရွှေ-

• n: စမ်းသပ်မှုအရေအတွက်
• k: အောင်မြင်မှုအရေအတွက်
• p- ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်နိုင်ခြေ
• _n C _k : n စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများရရှိရန် နည်းလမ်းများ

ဥပမာ၊ အကြွေစေ့ကို ၃ ကြိမ်လှန်တယ်ဆိုပါစို့။ ဤ 3 ကြိမ်အတွင်း 0 ဦးခေါင်းများရရှိရန် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125၊

n = 1 စမ်းသပ်သောအခါ၊ binomial ဖြန့်ဝေမှုသည် Bernoulli ဖြန့်ဖြူးမှုနှင့် ညီမျှသည်။

အရေးကြီးသောမှတ်စုများ

ဤသည်မှာ Bernoulli နှင့် Binomial ဖြန့်ဖြူးခြင်းဆိုင်ရာ အရေးကြီးသော မှတ်စုအချို့ဖြစ်သည်။

1. Bernoulli ဖြန့်ဖြူးမှုကို လိုက်လျှောက်သည့် ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင်သည် ဖြစ်နိုင်ချေတန်ဖိုးနှစ်ခုသာယူနိုင်သည်၊ သို့သော် binomial ဖြန့်ဝေမှုနောက်လိုက်သောကျပန်းကိန်းရှင်သည် တန်ဖိုးများစွာယူနိုင်သည်။

ဥပမာအားဖြင့်၊ အကြွေစေ့ပစ်ခြင်းတွင်၊ ကျွန်ုပ်တို့တွင် 0 သို့မဟုတ် 1 ခေါင်းများရှိသည်။ သို့သော် ဆက်တိုက် 5 ကြိမ်တွင် 0၊ 1၊ 2၊ 3၊ 4 သို့မဟုတ် 5 ခေါင်းများရှိသည်။

2. binomial ဖြန့်ဝေမှုအား လိုက်လျှောက်ရန် ကျပန်းကိန်းရှင်တစ်ခုအတွက်၊ Bernoulli စမ်းသပ်မှုတစ်ခုစီတွင် “ အောင်မြင်မှု” ၏ဖြစ်နိုင်ခြေသည် ညီမျှပြီး သီးခြားဖြစ်ရပါမည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် “ အောင်မြင်မှု” ကို ဦးခေါင်းပေါ်သို့ ဆင်းသက်ခြင်းဟု သတ်မှတ်ပါက၊ တစ်ကြိမ်စီတွင် အောင်မြင်မှု ဖြစ်နိုင်ခြေမှာ 0.5 ဖြစ်ပြီး မြှောက်ခြင်းတစ်ခုစီသည် သီးခြားဖြစ်သည် – မြှောက်ခြင်း၏ရလဒ်သည် အခြားရလဒ်အပေါ် သက်ရောက်မှုမရှိပါ။

ထပ်လောင်းအရင်းအမြစ်များ

Binomial စမ်းသပ်မှုများအကြောင်း နိဒါန်း
binomial ဖြန့်ဖြူးခြင်းအကြောင်း နိဒါန်း
binomial ဖြန့်ဖြူးခြင်း၏ ပုံသဏ္ဍာန်ကို နားလည်ခြင်း။