Binomial ဖြန့်ဖြူးရေးဇယားကိုဖတ်နည်း

binomial ဖြန့်ဖြူးရေးဇယား   binomial distribution နှင့်ဆက်စပ်သော ဖြစ်နိုင်ခြေများကို ပြသသော ဇယားတစ်ခုဖြစ်သည်။ binomial ဖြန့်ချီရေးဇယားကို အသုံးပြုရန်၊ သင်သည် တန်ဖိုးသုံးခုသာ လိုအပ်သည်-

• n: ကြိုးစားမှုအရေအတွက်
• r- n ကြိုးစားမှုအတွင်း “ အောင်မြင်မှု” အရေအတွက်
• p- ပေးထားသော စမ်းသပ်မှုတစ်ခု၏ အောင်မြင်နိုင်ခြေ

ဤနံပါတ်သုံးခုကိုအသုံးပြု၍ စမ်းသပ်မှု တစ်ခု စီတွင် အောင်မြင်မှုဖြစ်နိုင်ခြေ သည် p ဖြစ်သောအခါတွင် စမ်းသပ်မှုတစ်ခုစီတွင် အတိအကျ r အောင်မြင်မှုများရရှိရန်ဖြစ်နိုင်ခြေကို ရှာဖွေရန် binomial distribution table ကို အသုံးပြုနိုင်သည်။

အောက်ဖော်ပြပါနမူနာများသည် binomial distribution table ကို မည်သို့ဖတ်ရမည်ကို ဖော်ပြသည်။

ဥပမာ ၁

မေးခွန်း- Jessica သည် သူမ၏ အလွတ်ပစ်ရန် ကြိုးစားမှု၏ 60% ကို ပြုလုပ်သည်။ အကယ်၍ သူမသည် အလွတ်ပစ်ချက် 6 ကြိမ်ပြုလုပ်ပါက၊ သူမသည် 4 ကြိမ်တိတိပြုလုပ်နိုင်ခြေအဘယ်နည်း။

ဤမေးခွန်းကိုဖြေဆိုရန်၊ n = 6၊ r = 4 နှင့် p = 0.60 တို့ နှင့် ကိုက်ညီသော binomial ဖြန့်ချီရေးဇယားတွင် တန်ဖိုးကို ကျွန်ုပ်တို့ ရှာတွေ့နိုင်ပါသည် ။

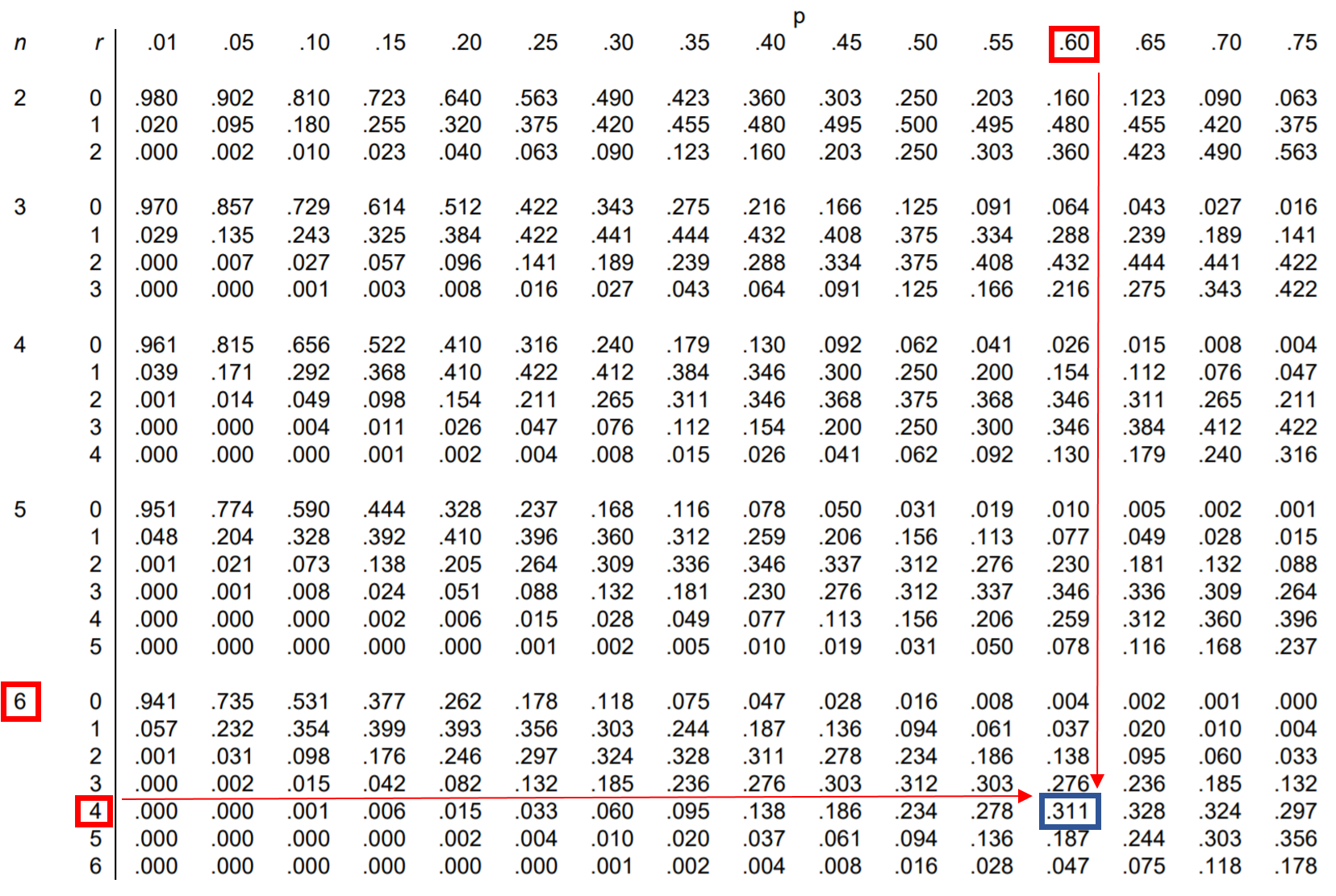
Jessica သည် အလွတ်ပစ်ခြင်း 6 ခုတွင် 4 ခုတိတိပြုလုပ်နိုင်ခြေသည် 0.311 ဖြစ်သည်။

ဥပမာ ၂

မေးခွန်း- Jessica သည် သူမ၏ အလွတ်ပစ်ရန် ကြိုးစားမှု၏ 60% ကို ပြုလုပ်သည်။ အကယ်၍ သူမသည် အလွတ်ပစ်ချက် 6 ကြိမ်ပြုလုပ်ပါက၊ သူမသည် 4 ထက်နည်းသော ဖြစ်နိုင်ခြေအဘယ်နည်း။

ဤဖြစ်နိုင်ခြေကိုရှာဖွေရန်၊ သင်သည် အမှန်တကယ်တွင် အောက်ပါဖြစ်နိုင်ခြေများကို ထည့်ရပါမည်။

P( 4 ထက်နည်းသည် ) = P ( 0 ) + P ( 1 ) + P ( 2 ) + P ( 3 )

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဤဖြစ်နိုင်ခြေလေးမျိုးထဲမှ တစ်ခုစီကို binomial distribution table တွင် ရှာဖွေပြီး ၎င်းတို့ကို ပေါင်းထည့်နိုင်သည်-

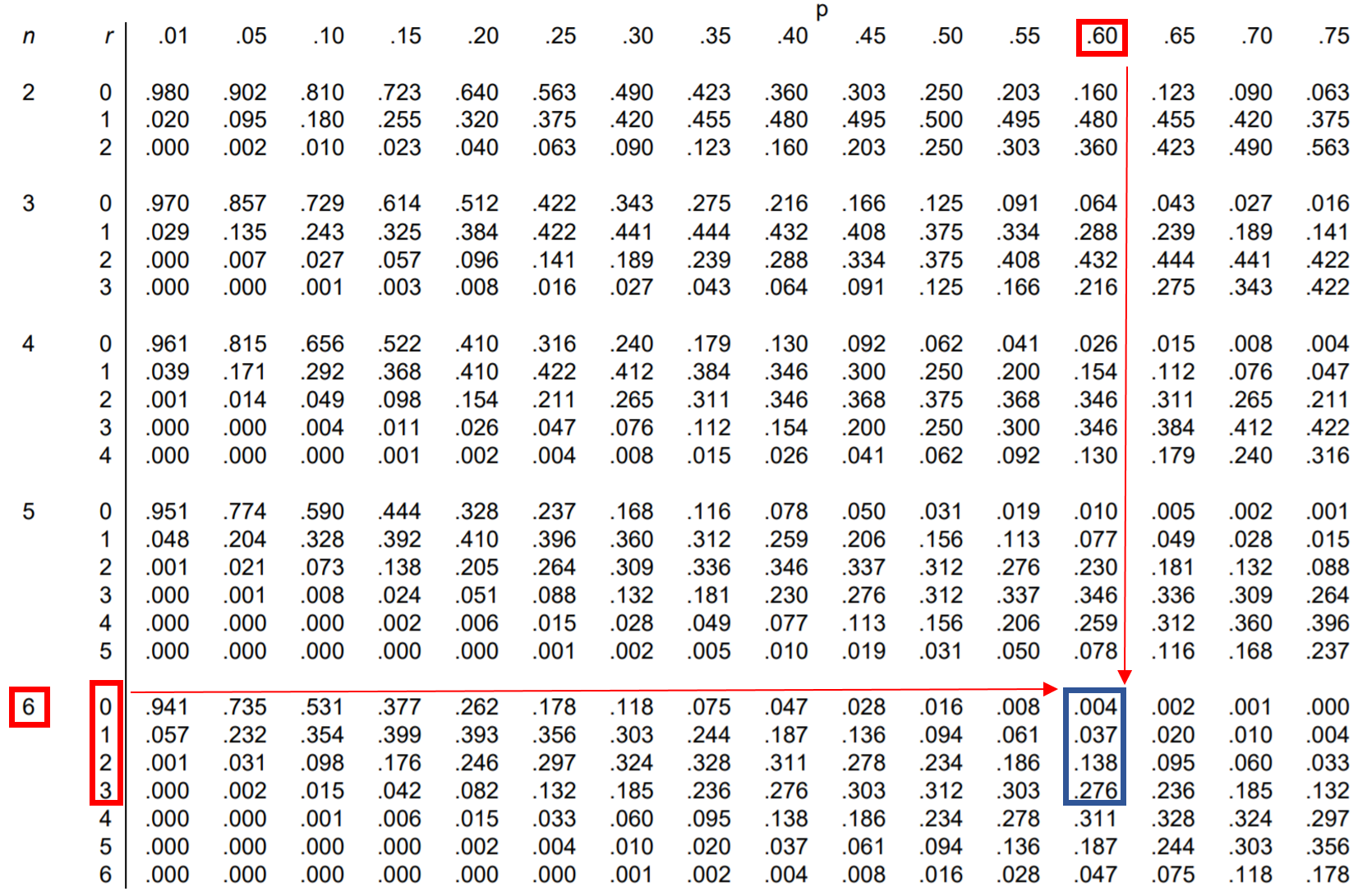
ဇယားမှ P(4 ထက်နည်းသည်) = .004 + .037 + .138 + .276 = 0.455 ။

Jessica သည် အလွတ်ပစ်ခြင်း 4 ခုထက်နည်းသော ဖြစ်နိုင်ခြေမှာ 0.455 ဖြစ်သည်။

ဥပမာ ၃

မေးခွန်း- Jessica သည် သူမ၏ အလွတ်ပစ်ရန် ကြိုးစားမှု၏ 60% ကို ပြုလုပ်သည်။ အကယ်၍ သူမသည် လွှတ်တင်ခြင်း 6 ကြိမ်ပြုလုပ်ပါက၊ သူမသည် 4 ကြိမ် သို့မဟုတ် ထို့ထက်ပို၍ပြုလုပ်နိုင်ခြေအဘယ်နည်း။

ဤဖြစ်နိုင်ခြေကိုရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါဖြစ်နိုင်ခြေများကို ထည့်ရပါမည်။

P(လုပ် 4 သို့မဟုတ် ထို့ထက်ပိုသည်) = P(4) + P(5) + P(လုပ် 6)

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဤဖြစ်နိုင်ခြေ သုံးခုအနက် တစ်ခုစီကို binomial distribution table တွင် ရှာဖွေပြီး ၎င်းတို့ကို ပေါင်းထည့်နိုင်သည်-

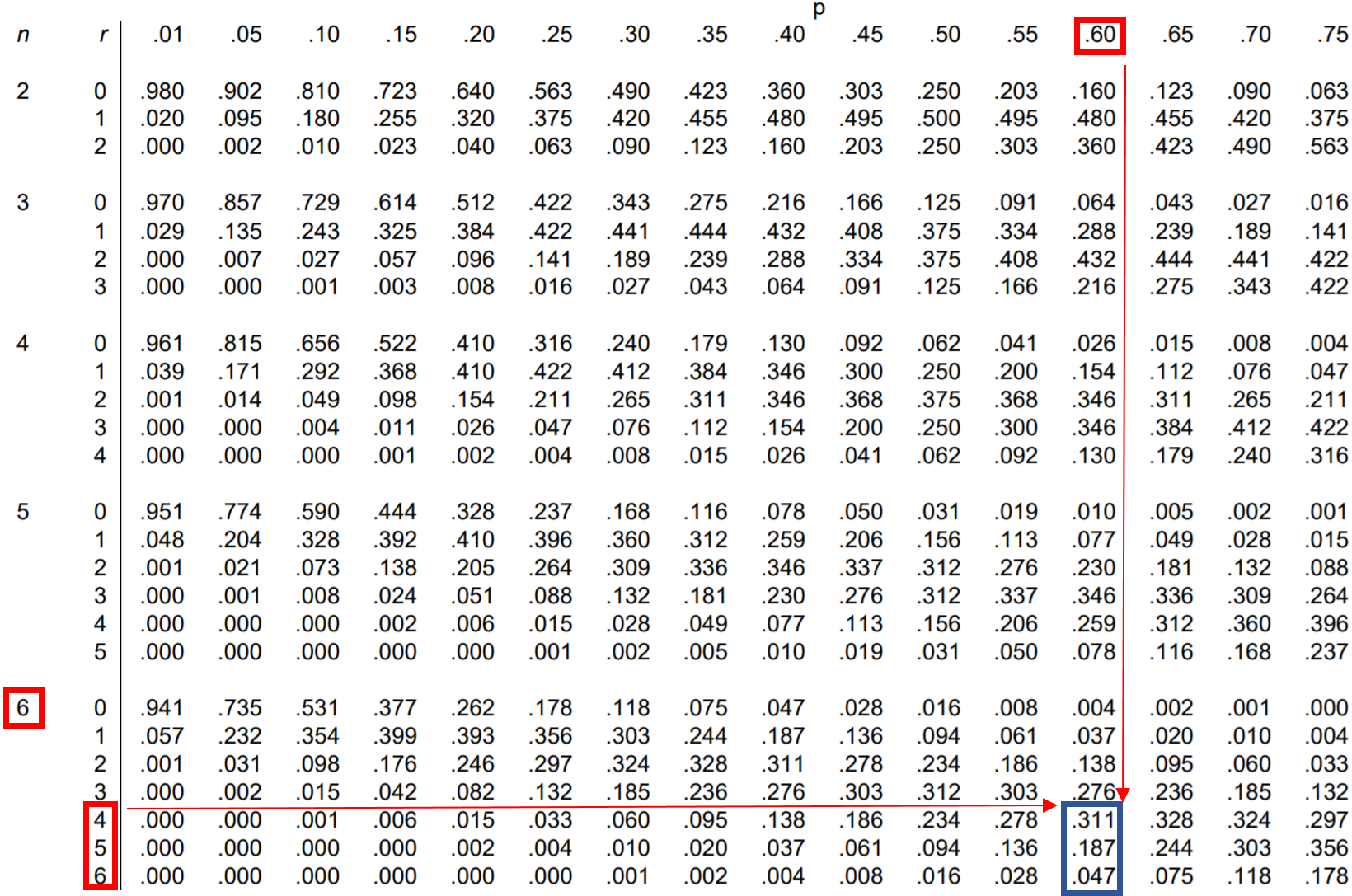
ဇယားမှ P(4 သို့မဟုတ် ထို့ထက်ပိုသော) = .311 + .187 + .047 = 0.545 ။

Jessica သည် အလွတ်ပစ်ခြင်း 4 ခု သို့မဟုတ် ထို့ထက်ပို၍ ပြုလုပ်နိုင်သည့် ဖြစ်နိုင်ခြေမှာ 0.545 ဖြစ်သည်။