Binomial ဖြန့်ဖြူးခြင်းအတွက် နိဒါန်းတစ်ခု
binomial distribution သည် စာရင်းဇယားများတွင် ရေပန်းအစားဆုံး ဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။ binomial ဖြန့်ဖြူးမှုကို နားလည်ရန်၊ ၎င်းသည် binomial စမ်းသပ်မှုများကို ဦးစွာနားလည်ရန် ကူညီပေးသည်။
Binomial စမ်းသပ်မှုများ
binomial စမ်းသပ်ချက် သည် အောက်ပါဂုဏ်သတ္တိများပါရှိသော စမ်းသပ်မှုတစ်ခုဖြစ်သည်။
- စမ်းသပ်မှုတွင် ထပ်ခါတလဲလဲ စမ်းသပ်မှုများ ပါဝင်သည်။
- စမ်းသပ်မှုတစ်ခုစီတွင် ဖြစ်နိုင်ချေရလဒ်နှစ်ခုသာရှိသည်။
- စမ်းသပ်မှု တစ်ခုစီအတွက် အောင်မြင်မှုဖြစ်နိုင်ခြေသည် တူညီသည်။
- စမ်းသပ်မှုတိုင်းသည် သီးခြားဖြစ်သည်။
binomial စမ်းသပ်မှု၏ အထင်ရှားဆုံး ဥပမာမှာ အကြွေစေ့ပစ်ခြင်း ဖြစ်သည်။ ဥပမာ၊ အကြွေစေ့ကို ၁၀ ကြိမ်လှန်တယ်ဆိုပါစို့။ ၎င်းသည် အောက်ဖော်ပြပါ ဂုဏ်သတ္တိလေးခုပါရှိသောကြောင့် ၎င်းတွင် binomial စမ်းသပ်မှုတစ်ခုဖြစ်သည်။
- စမ်းသပ်မှုတွင် ထပ်ခါတလဲလဲ စမ်းသပ်မှုများ ပါဝင်သည် – စမ်းသပ်မှု 10 ခုရှိသည်။
- စမ်းသပ်မှုတစ်ခုစီတွင် ဖြစ်နိုင်ခြေရှိသော ရလဒ်နှစ်ခုသာရှိသည်- ဦးခေါင်း သို့မဟုတ် အမြီးများ။
- စမ်းသပ်မှု တစ်ခုစီအတွက် အောင်မြင်မှုဖြစ်နိုင်ခြေသည် တူညီသည်။ ကျွန်ုပ်တို့သည် “ အောင်မြင်မှု” ကို ဆင်းသက်သည့် ဦးခေါင်းများအဖြစ် သတ်မှတ်ပါက၊ စမ်းသပ်မှုတစ်ခုစီအတွက် အောင်မြင်နိုင်ခြေသည် 0.5 အတိအကျဖြစ်သည်။
- စမ်းသပ်မှုတစ်ခုစီသည် သီးခြားဖြစ်သည်- အကြွေစေ့တစ်ခုပစ်ခြင်း၏ရလဒ်သည် အခြားအကြွေစေ့ပစ်ခြင်း၏ရလဒ်အပေါ် သက်ရောက်မှုမရှိပါ။
binomial ဖြန့်ဖြူးမှု
binomial distribution သည် n binomial စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများ ရရှိရန် ဖြစ်နိုင်ခြေကို ဖော်ပြသည်။
ကျပန်း variable X သည် binomial distribution ကို လိုက်နာပါက၊ X = k အောင်မြင်မှု ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-
P(X=k) = n C k * p k * (1-p) nk
ရွှေ-
- n: စမ်းသပ်မှုအရေအတွက်
- k: အောင်မြင်မှုအရေအတွက်
- p- ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်နိုင်ခြေ
- n C k : n စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများရရှိရန် နည်းလမ်းများ
ဥပမာ၊ အကြွေစေ့ကို ၃ ကြိမ်လှန်တယ်ဆိုပါစို့။ ဤ 3 ကြိမ်တွင် 0၊ 1၊ 2 နှင့် 3 ခေါင်းများကို ရယူရန် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ရန် အထက်ဖော်ပြပါ ဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။
P(X=0) = 3 C 0 * 0.5 0 * (1-0.5) 3-0 = 1 * 1 * (0.5) 3 = 0.125၊
P(X=1) = 3 C 1 * 0.5 1 * (1-0.5) 3-1 = 3 * 0.5 * (0.5) 2 = 0.375၊
P(X=2) = 3 C 2 * 0.5 2 * (1-0.5) 3-2 = 3 * 0.25 * (0.5) 1 = 0.375၊
P(X=3) = 3 C 3 * 0.5 3 * (1-0.5) 3-3 = 1 * 0.125 * (0.5) 0 = 0.125၊
မှတ်ချက် – ဥပမာတစ်ခုစီ အတွက် nCk ကို တွက်ချက်ရန် ဤ ပေါင်းစပ်ဂဏန်းတွက်စက်ကို ကျွန်ုပ်တို့အသုံးပြုခဲ့သည် ။
ဤဖြစ်နိုင်ချေ ဖြန့်ဖြူးမှုကို မြင်သာစေရန် ရိုးရှင်းသော ဟီစတိုဂရမ်ကို ဖန်တီးနိုင်သည်-
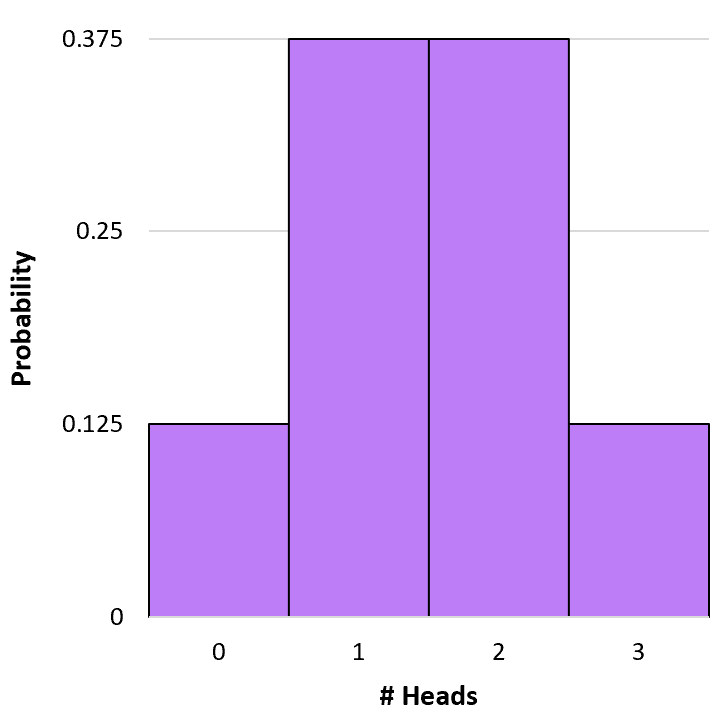
တိုးပွားလာသော binomial ဖြစ်နိုင်ခြေများကို တွက်ချက်ခြင်း။
အထက်ဖော်ပြပါဖော်မြူလာကို အသုံးပြု၍ binomial probability တစ်ခုတည်း (ဥပမာ- ဒင်္ဂါးတစ်ပြား၏ဖြစ်နိုင်ခြေသည် အထက်ဖော်ပြပါပုံသေနည်းကို အသုံးပြု၍ အကြွေစေ့ ၃ ကြိမ်မှ ၁ ကြိမ်) ပေါ်လာနိုင်ချေကို တွက်ချက်ရန် ရိုးရှင်းသော်လည်း၊ တိုးပွားလာသော binomial ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန်အတွက် ကျွန်ုပ်တို့သည် တစ်ဦးချင်းဖြစ်နိုင်ချေများကို ပေါင်းထည့်ရန် လိုအပ်ပါသည်။
ဥပမာအားဖြင့်၊ အကြွေစေ့ ၃ ကြိမ်မှ ၁ ကြိမ် သို့မဟုတ် ထိုထက်နည်းသော ဒင်္ဂါးပြားတစ်ခု ခေါင်းပေါ်တက်လာနိုင်ခြေကို ကျွန်ုပ်တို့ သိချင်သည်ဆိုကြပါစို့။ ဤဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုပါမည်။
P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 ။
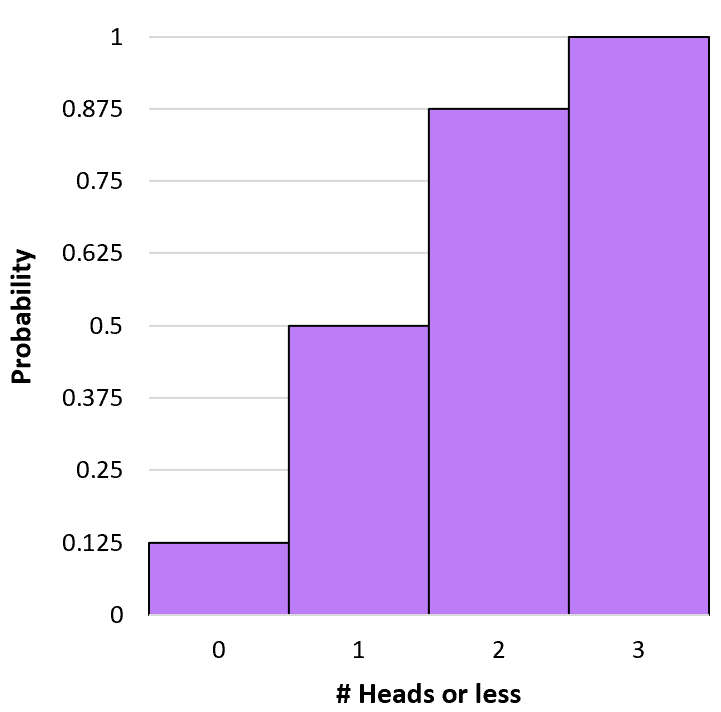
ဖြစ်နိုင်ခြေများစွာကို ပေါင်းထည့်ခြင်းတို့ ပါဝင်သောကြောင့် ၎င်းကို စုဆောင်းဖြစ်နိုင်ခြေ ဟု ခေါ်သည်။ အလားတူ ဖော်မြူလာကို အသုံးပြု၍ ရလဒ်တစ်ခုစီအတွက် k ဦးခေါင်းများရရှိခြင်း သို့မဟုတ် ပိုနည်းသော ဖြစ်နိုင်ခြေကို တွက်ချက်နိုင်သည်-
P(X≤0) = P(X=0) = 0.125 ။
P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 ။
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0.125 + 0.375 + 0.375 = 0.875 ။
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 ။
ဤစုစည်းဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို မြင်သာစေရန် ဟီစတိုဂရမ်တစ်ခု ဖန်တီးနိုင်သည်-
Binomial Probability ဂဏန်းတွက်စက်
ကျွန်ုပ်တို့သည် သေးငယ်သော ဂဏန်းများဖြင့် အလုပ်လုပ်သောအခါ (ဥပမာ- အကြွေစေ့ 3 ပြားကို လွှင့်ပစ်ခြင်း) သည် binomial ဖြစ်နိုင်ခြေများကို လက်ဖြင့် တွက်ချက်ရန် ကျိုးကြောင်းဆီလျော်ပါသည်။ သို့သော်၊ ကျွန်ုပ်တို့သည် ပိုကြီးသော ဂဏန်းများဖြင့် အလုပ်လုပ်သောအခါ (ဥပမာ 100 သရေကျခြင်း)၊ ဖြစ်နိုင်ခြေများကို လက်ဖြင့် တွက်ချက်ရန် ခက်ခဲနိုင်သည်။ ဤကိစ္စများတွင်၊ အောက်ဖော်ပြပါကဲ့သို့ binomial probability calculator ကို အသုံးပြုရန် အထောက်အကူဖြစ်နိုင်သည်။
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် အကြွေစေ့ n = 100 ကြိမ် ပစ်ချလိုက်သည်ဆိုပါစို့၊ ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် ဦးခေါင်းပေါ်တက်ခြင်း၏ ဖြစ်နိုင်ခြေမှာ p = 0.5 ဖြစ်ပြီး၊ ၎င်းသည် ခေါင်းပေါ် k = 43 ကြိမ် သို့မဟုတ် ထိုထက်နည်းသော ဖြစ်နိုင်ခြေကို သိလိုပါသည်။
P(X= 43 ) = 0.03007
P(X< 43 ) = 0.06661
P( X≤43 ) = 0.09667
P(X> 43 ) = 0.90333
P( X≥43 ) = 0.93339
ဤသည်မှာ ရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-
- ခေါင်းပေါ်တက်လာသော အကြွေစေ့၏ဖြစ်နိုင်ခြေသည် 43 ကြိမ်တိတိ 0.03007 ဖြစ်သည်။
- 43 ကြိမ်ထက်နည်းသောအကြွေစေ့များ၏ဖြစ်နိုင်ခြေသည် 0.06661 ဖြစ်သည်။
- 43 ကြိမ် သို့မဟုတ် ထိုထက်နည်းသော ဒင်္ဂါးပြား၏ ဖြစ်နိုင်ခြေသည် 0.09667 ဖြစ်သည်။
- အကြွေစေ့ခေါင်းပေါ်တက်လာနိုင်ခြေ 43 ကြိမ်ထက် 0.90333 ဖြစ်ပါတယ်။
- အကြွေစေ့ ၄၃ ကြိမ် သို့မဟုတ် ထို့ထက်ပို၍ ခေါင်းပေါ်တက်လာနိုင်ခြေမှာ 0.93339 ဖြစ်သည်။
binomial ဖြန့်ဖြူးခြင်း၏ ဂုဏ်သတ္တိများ
binomial ဖြန့်ဖြူးမှုတွင် အောက်ပါဂုဏ်သတ္တိများ ရှိသည်။
ဖြန့်ဖြူးမှု၏ ဆိုလိုရင်းမှာ μ = np ဖြစ်သည်။
ဖြန့်ဝေမှု၏ကွဲလွဲမှုသည် σ 2 = np(1-p)
ဖြန့်ဖြူးမှု၏စံသွေဖည်မှုမှာ σ = √ np(1-p) ဖြစ်သည်။
ဥပမာ၊ အကြွေစေ့ကို ၃ ကြိမ်လောက် ပစ်တယ်ဆိုပါစို့။ p = ဒင်္ဂါးပြားခေါင်းပေါ်ကျသော ဖြစ်နိုင်ခြေကို ကြည့်ပါ။
ကျွန်ုပ်တို့မျှော်လင့်ထားသော ပျမ်းမျှဦးခေါင်းအရေအတွက်မှာ μ = np = 3*.5 = 1.5 ဖြစ်သည်။
ကျွန်ုပ်တို့မျှော်လင့်ထားသော head count varianance သည် σ 2 = np(1-p) = 3*.5*(1-.5) = 0.75 ဖြစ်သည် ။
Binomial Distribution Practice ပြဿနာများ
binomial ဖြန့်ဖြူးခြင်းဆိုင်ရာ သင်၏အသိပညာကို စမ်းသပ်ရန် အောက်ပါအလေ့အကျင့်ပြဿနာများကို အသုံးပြုပါ။
ပြဿနာ ၁
မေးခွန်း- Bob သည် သူ၏ အလွတ်ပစ်ရန် ကြိုးစားမှု 60% ကို ပြုလုပ်သည်။ အကယ်၍ သူသည် အလွတ်ပစ်ချက် 12 ကြိမ်ပြုလုပ်ပါက၊ သူ 10 တိတိပြုလုပ်နိုင်သည့် ဖြစ်နိုင်ခြေမှာ အဘယ်နည်း။
အဖြေ- p = 0.6၊ n = 12 နှင့် k = 10 ဖြင့် အထက်တွင်ရှိသော binomial distribution calculator ကို အသုံးပြု၍ P(X=10) = 0.06385 ကို ကျွန်ုပ်တို့ တွေ့ရှိရပါသည်။
ပြဿနာ ၂
မေးခွန်း- Jessica သည် အကြွေစေ့ကို ၅ ကြိမ်လှန်သည်။ အကြွေစေ့ ၂ ကြိမ် သို့မဟုတ် ထိုထက်နည်းသော အကြွေစေ့များ ခေါင်းပေါ်တက်လာနိုင်ခြေ မည်မျှရှိသနည်း။
အဖြေ- p = 0.5၊ n = 5 နှင့် k = 2 ဖြင့် အထက်တွင်ရှိသော binomial distribution calculator ကို အသုံးပြု၍ P(X≤2) = 0.5 ကို ကျွန်ုပ်တို့ တွေ့ရှိပါသည်။
ပြဿနာ ၃
မေးခွန်း- ပေးထားသော ကျောင်းသားအား ကောလိပ်တစ်ခုသို့ လက်ခံမည့် ဖြစ်နိုင်ခြေမှာ 0.2 ဖြစ်သည်။ ကျောင်းသား 10 ဦး လျှောက်ထားပါက 4 ဦးထက်ပိုလက်ခံမည့် ဖြစ်နိုင်ခြေ မည်မျှရှိသနည်း။
အဖြေ- p = 0.2၊ n = 10 နှင့် k = 4 ဖြင့် အထက်ဖော်ပြပါ binomial distribution calculator ကို အသုံးပြု၍ P(X>4) = 0.03279 ကို ကျွန်ုပ်တို့ တွေ့ရှိပါသည်။
ပြဿနာ ၄
မေးခွန်း- သင်သည် အကြွေစေ့ကို ၁၂ ကြိမ်လှန်ပါ။ ပေါ်လာမည့် ပျမ်းမျှဦးခေါင်းအရေအတွက်က ဘယ်လောက်လဲ။
အဖြေ- binomial distribution တစ်ခု၏ ဆိုလိုရင်းကို μ = np အဖြစ် တွက်ချက်ထားကြောင်း မှတ်သားပါ။ ဒီတော့ μ = 12*0.5 = 6 ခေါင်း ။
ပြဿနာ ၅
မေးခွန်း- Mark သည် သူကြိုးစားမှု၏ 10% ဖြင့် အိမ်ပြန်ပြေးခြင်း ဖြစ်သည်။ သူသတ်မှတ်ထားသောဂိမ်းတစ်ခုတွင် 5 ကြိမ်ကြိုးစားပါက၊ သူတိုက်မိသည့်အိမ်ကွင်းအရေအတွက်ကွာခြားချက်မှာ အဘယ်နည်း။
အဖြေ- binomial distribution တစ်ခု၏ ကွဲလွဲမှုကို σ 2 = np(1-p) အဖြစ် တွက်ချက်ထားကြောင်း သတိရပါ။ ထို့ကြောင့် σ2 = 6*.1*(1-.1) = 0.54 ။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ ဆောင်းပါးများသည် မတူညီသော စာရင်းအင်းဆော့ဖ်ဝဲလ်တွင် binomial ဖြန့်ဖြူးနည်းကို အသုံးပြုနည်းကို လေ့လာရန် ကူညီပေးနိုင်ပါသည်။