Binomial ဖြန့်ဖြူးခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကိန်းဂဏန်းများ ကိန်းဂဏန်းများ ဖြန့်ဖြူးခြင်းမှာ အဘယ်အရာနှင့် ၎င်းကို အသုံးပြုရကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့် သင်သည် binomial distribution ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ binomial distributions ၏ ဥပမာများနှင့် ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂုဏ်သတ္တိများကို သင်တွေ့လိမ့်မည်။ ထို့အပြင်၊ သင်သည် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် binomial ဖြန့်ဖြူးခြင်း၏ ဖြစ်နိုင်ခြေမှန်သမျှကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

binomial ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

binomial distribution သည် အောင်မြင်မှု၏ ဆက်တိုက်ဖြစ်နိုင်ခြေရှိသော လွတ်လပ်သော၊ dichotomous စမ်းသပ်မှုများကို ဆက်တိုက်လုပ်ဆောင်သောအခါ အောင်မြင်မှုအရေအတွက်ကို ရေတွက်သည့် ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

တစ်နည်းဆိုရသော်၊ binomial distribution သည် Bernoulli စမ်းသပ်မှု၏ အစီအစဥ်တစ်ခု၏ အောင်မြင်သောရလဒ်အရေအတွက်ကို ဖော်ပြသည့် ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

Bernoulli စမ်းသပ်မှုသည် “ အောင်မြင်မှု” နှင့် “ ကျရှုံးခြင်း” ဖြစ်နိုင်သောရလဒ်နှစ်ခုရှိသည်သောစမ်းသပ်မှုတစ်ခုဖြစ်ကြောင်းသတိရပါ။ ထို့ကြောင့်၊ “ အောင်မြင်မှု” ၏ဖြစ်နိုင်ခြေသည် p ဖြစ်ပါက၊ “ ကျရှုံးခြင်း” ဖြစ်နိုင်ခြေမှာ q=1-p ဖြစ်သည်။

ယေဘူယျအားဖြင့်၊ စမ်းသပ်မှုတစ်ခုစီ၏အောင်မြင်နိုင်ခြေကို p သည် parameter n ဖြင့်သတ်မှတ်ထားပြီး၊ p သည်စမ်းသပ်မှုတစ်ခုစီ၏အောင်မြင်နိုင်ခြေဖြစ်သည်။ ထို့ကြောင့်၊ binomial ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သော ကျပန်းကိန်းရှင်ကို အောက်ပါအတိုင်း ရေးသားထားသည်။

$X\sim\text{Bin}(n,p)$

binomial ဖြန့်ဝေမှုတွင်၊ အတိအကျတူညီသောစမ်းသပ်ချက်သည် အကြိမ် n ကြိမ်ဖြစ်ပြီး စမ်းသပ်မှုများသည် တစ်ခုနှင့်တစ်ခု အမှီအခိုကင်းသောကြောင့် စမ်းသပ်မှုတစ်ခုစီ၏အောင်မြင်နိုင်ခြေသည် တူညီသည် (p) ကိုသတိပြုပါ။

binomial distribution ကို binomial distribution ဟုလည်း ခေါ်နိုင်သည်။

Binomial Distribution နမူနာများ

binomial distribution ၏ အဓိပ္ပါယ်ကို ကျွန်ုပ်တို့တွေ့မြင်ပြီးသည်နှင့်၊ သဘောတရားကို ပိုမိုနားလည်ရန် ဤဖြန့်ဖြူးမှုအမျိုးအစားကို လိုက်နာသော variables အများအပြားကို တွေ့ရမည်ဖြစ်ပါသည်။

အကြွေစေ့ကို 25 ကြိမ်ပစ်သောအခါ ခေါင်းများပေါ်လာသည့် အကြိမ်အရေအတွက်။
ဘတ်စကက်ဘောကစားသမားတစ်ဦးသည် တစ်နေရာတည်းမှ ခြင်းတောင်းဆီသို့ အကြိမ် 60 ပစ်ခတ်သောအခါ ရိုက်ချက်အရေအတွက်။
အကြိမ် 30 လှိမ့်ခြင်းဖြင့် နံပါတ် 6 ကိုရရှိသည်။
စာမေးပွဲဖြေဆိုနေသည့် ကျောင်းသား စုစုပေါင်း ၅၀ ဦးအနက်မှ အောင်ချက်အရေအတွက်။
နမူနာထုတ်ကုန် 100 တွင် ချွတ်ယွင်းချက်ယူနစ်အရေအတွက်။

Binomial ဖြန့်ဖြူးမှုဖော်မြူလာ

ကန့်သတ်ချက်များ x၊ n၊ p တို့ကို ပေးထားသည့် binomial distribution ၏ ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်ကို x အမြှောက် p ^x အမြှောက် (1-p) ^nx တွင် n ၏ပေါင်းစပ်ဂဏန်းအဖြစ် သတ်မှတ်သည်။

ထို့ကြောင့်၊ binomial distribution ၏ ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် ဖော်မြူလာမှာ –

👉 binomial ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်သော variable ၏ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါ calculator ကိုသင်အသုံးပြုနိုင်ပါသည်။

အခြားတစ်ဖက်တွင်၊ binomial distribution ၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေကို မေးခွန်းရှိ အောင်မြင်မှုအရေအတွက်နှင့် ယခင်ဖြစ်နိုင်ခြေအားလုံးကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်သည်။ ထို့ကြောင့်၊ binomial ဖြန့်ဖြူးမှု၏ စုစည်းဖြစ်နိုင်ခြေကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

binomial ဖြန့်ဖြူးမှုအပေါ် ဖြေရှင်းထားသော လေ့ကျင့်ခန်း

အကြွေစေ့ကို 10 ကြိမ်လောက်ပစ်တယ်၊ 6 ခေါင်းရဖို့ ဖြစ်နိုင်ခြေဘယ်လောက်ရှိလဲ။

လွှတ်တင်မှုအားလုံးသည် တစ်ခုနှင့်တစ်ခု သီးခြားဖြစ်ပြီး အောင်မြင်နိုင်ခြေလည်း တူညီသောကြောင့် ဤပြဿနာရှိ ကိန်းရှင်သည် binomial ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်သည်။

တိကျစွာပြောရလျှင် အောင်မြင်နိုင်ခြေ 50% သည် ဖြစ်နိုင်ချေရလဒ် နှစ်ခုအနက်မှ တစ်ခုကို အောင်မြင်သည်ဟု ယူဆသောကြောင့်ဖြစ်သည်။

$p=\cfrac{1}{2}=0,5$

ထို့ကြောင့်၊ ဤလေ့ကျင့်ခန်းအတွက် ဖြန့်ဖြူးမှုသည် စုစုပေါင်းစမ်းသပ်ချက် 10 ခုနှင့် ဖြစ်နိုင်ခြေ 0.5 ပါရှိသော binomial တစ်ခုဖြစ်သည်။

$X\sim\text{Bin}(10 ; 0,5)$

ထို့ကြောင့်၊ ခေါင်းခြောက်လုံးရနိုင်ခြေကို ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် binomial distribution formula ကို အသုံးပြုရန် လိုအပ်ပါသည်။

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

ထို့ကြောင့်၊ အကြွေစေ့တစ်စေ့ကိုဆယ်ကြိမ်ပစ်ခြင်းဖြင့် ခေါင်းခြောက်လုံးတိတိရနိုင်ခြေသည် 20.51% ဖြစ်သည်။

binomial ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

binomial ဖြန့်ဖြူးမှုတွင် အောက်ပါလက္ခဏာများ ရှိသည်။

binomial distribution ကို ဘောင်နှစ်ခုဖြင့် သတ်မှတ်သည်- n သည် Bernoulli စမ်းသပ်မှု စုစုပေါင်း အရေအတွက်ဖြစ်ပြီး အခြားတစ်ဖက်တွင် p သည် Bernoulli စမ်းသပ်မှုတစ်ခုစီ၏ အောင်မြင်မှုဖြစ်နိုင်ခြေဖြစ်သည်။

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

binomial ဖြန့်ဖြူးမှု၏ပျမ်းမျှသည် စမ်းသပ်မှုတစ်ခုစီ၏အောင်မြင်နိုင်ခြေဖြင့် မြှောက်ထားသော စုစုပေါင်းစမ်းသပ်မှုအရေအတွက်နှင့် ညီမျှသည်။ ထို့ကြောင့်၊ binomial distribution တစ်ခု၏ ဆိုလိုရင်းကို တွက်ချက်ရန် n နှင့် p ကို မြှောက်ရပါမည်။

$E[X]=n\cdot p$

binomial ဖြန့်ဝေမှု၏ကွဲလွဲမှုသည် အောင်မြင်နိုင်ခြေနှင့် ကျရှုံးမှုဖြစ်နိုင်ခြေတို့ဖြင့် မြှောက်ထားသော စမ်းသပ်မှုစုစုပေါင်းအရေအတွက်နှင့် ညီမျှသည်။

$Var(X)=n\cdot p\cdot (1-p)$

binomial ဖြန့်ဖြူးမှု၏ ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

အလားတူ၊ binomial ဖြန့်ဖြူးမှု၏ စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

တူညီသောဖြစ်နိုင်ခြေရှိသော လွတ်လပ်သော binomial ဖြန့်ဝေမှုနှစ်ခု၏ပေါင်းလဒ်သည် တူညီသောဖြစ်နိုင်ခြေတန်ဖိုး p နှင့် n တို့သည် တူညီသောဖြစ်နိုင်ခြေတန်ဖိုးရှိသော binomial ဖြန့်ဖြူးမှုတစ်ခုနှင့် ညီမျှသည်။

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

Bernoulli ဖြန့်ဖြူးမှုသည် n=1 ၊ ဆိုလိုသည်မှာ စမ်းသပ်မှုတစ်ခုသာ လုပ်ဆောင်သည့် binomial distribution ၏ အထူးကိစ္စရပ်ဖြစ်သည်။

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_{အကယ်၍} _X 1 , _X ₂ ,… , X _k သည် သီးခြားကျပန်း ကိန်းရှင်များ ဖြစ်ပါက၊

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

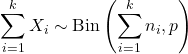
Binomial ဖြန့်ဝေဂဏန်းတွက်စက်

ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ binomial ဖြန့်ဖြူးမှု၏ p ၊ n နှင့် x တို့၏တန်ဖိုးများကို ထည့်သွင်းပါ။ သင်သည် တွက်ချက်လိုသော ဖြစ်နိုင်ခြေကို ရွေးချယ်ပြီး ဒဿမခွဲထွက်တစ်ခုအနေဖြင့် ဥပမာအားဖြင့် 0.1667 အစက်ကို အသုံးပြု၍ နံပါတ်များကို ရိုက်ထည့်ရန် လိုအပ်သည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။