Python တွင် binomial distribution ကိုအသုံးပြုနည်း

binomial distribution သည် စာရင်းဇယားများတွင် အသုံးအများဆုံး ဖြန့်ဝေမှုများထဲမှ တစ်ခုဖြစ်သည်။ ၎င်းသည် n binomial စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများရရှိရန် ဖြစ်နိုင်ခြေကို ဖော်ပြသည်။

ကျပန်း variable X သည် binomial distribution ကို လိုက်နာပါက၊ X = k အောင်မြင်မှု ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ရွှေ-

• n: စမ်းသပ်မှုအရေအတွက်
• k: အောင်မြင်မှုအရေအတွက်
• p- ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်နိုင်ခြေ
• _n C _k : n စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများရရှိရန် နည်းလမ်းများ

ဤသင်ခန်းစာတွင် Python တွင် binomial distribution ကို အသုံးပြုပုံကို ရှင်းပြထားသည်။

binomial distribution ကို ဘယ်လိုထုတ်လုပ်မလဲ။

numpy library ၏ random.binomial လုပ်ဆောင်ချက်ကို အသုံးပြု၍ binomial ဖြန့်ဖြူးမှုနောက်တွင်ရှိသော တန်ဖိုးများ array တစ်ခုကို သင်ဖန်တီးနိုင်သည်-

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

ရလဒ်ဇယားရှိ ဂဏန်းတစ်ခုစီသည် စမ်းသပ်မှု 10 ခု အတွင်း ကြုံတွေ့ခဲ့ရသော “ အောင်မြင်မှုများ” အရေအတွက်ကို ကိုယ်စားပြုပြီး ပေးထားသော အစမ်းသုံးမှုတွင် အောင်မြင်နိုင်ခြေမှာ 0.25 ဖြစ်နိုင်ပါသည်။

binomial distribution ကို အသုံးပြု၍ ဖြစ်နိုင်ခြေ တွက်ချက်နည်း

scipy library ၏ binom လုပ်ဆောင်ချက်ကို အသုံးပြု၍ binomial ဖြစ်နိုင်ခြေဆိုင်ရာ မေးခွန်းများကိုလည်း သင်ဖြေနိုင်ပါသည်။

မေးခွန်း 1- Nathan သည် ၎င်း၏ အလွတ်ပစ်ရန် 60% ကို ပြုလုပ်သည်။ အကယ်၍ သူသည် အလွတ်ပစ်ချက် 12 ကြိမ်ပြုလုပ်ပါက၊ သူ 10 တိတိပြုလုပ်နိုင်သည့် ဖြစ်နိုင်ခြေမှာ အဘယ်နည်း။

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Nathan သည် အလွတ်ပစ်လွှတ်ခြင်း 10 ကြိမ်တိတိ ပြုလုပ်နိုင်ခြေသည် 0.0639 ဖြစ်သည်။

မေးခွန်း 2- မာတီသည် အကြွေစေ့ကို 5 ကြိမ်လှန်သည်။ အကြွေစေ့ ၂ ကြိမ် သို့မဟုတ် ထိုထက်နည်းသော အကြွေစေ့များ ခေါင်းပေါ်တက်လာနိုင်ခြေ မည်မျှရှိသနည်း။

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

အကြွေစေ့ ၂ ကြိမ် သို့မဟုတ် ထိုထက်နည်းသော ဒင်္ဂါးပြားသည် 0.5 ဖြစ်သည်။

မေးခွန်း 3- လူတစ်ဦးချင်းစီ၏ 70% သည် သတ်မှတ်ထားသော ဥပဒေတစ်ခုကို ထောက်ခံကြောင်း ကျွန်ုပ်တို့သိပါသည်။ အကယ်၍ လူ ၁၀ ဦးကို ကျပန်းရွေးချယ်ခံရပါက၊ ၎င်းတို့ထဲမှ ၄ ဦးမှ ၆ ဦးကြားသည် ဥပဒေကို ထောက်ခံနိုင်ခြေ မည်မျှရှိသနည်း။

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

4 နှင့် 6 အကြား ကျပန်းရွေးချယ်ထားသော ပုဂ္ဂိုလ်များသည် ဥပဒေကို ထောက်ခံသည့် ဖြစ်နိုင်ခြေမှာ 0.3398 ဖြစ်သည်။

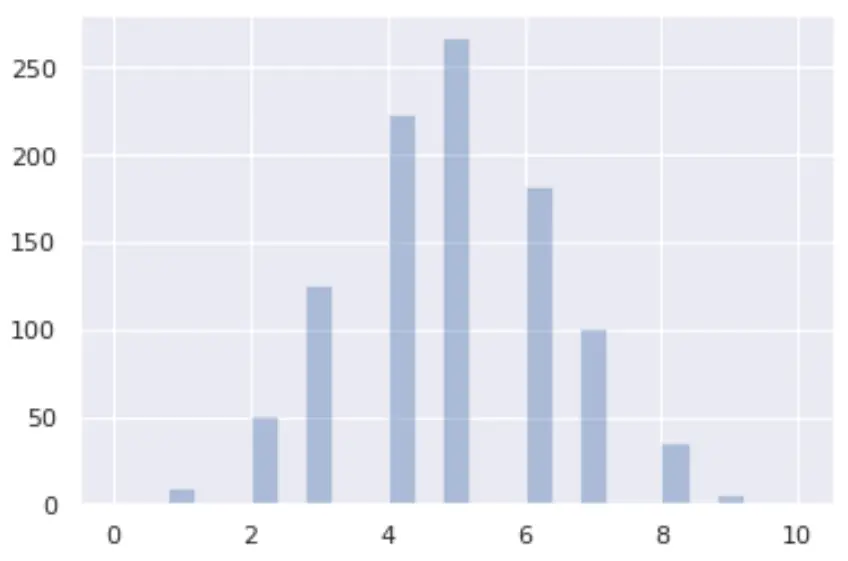
binomial ဖြန့်ဖြူးမှုကို မြင်ယောင်ပုံ

ပင်လယ်မွေး နှင့် matplotlib စာကြည့်တိုက်များကို အသုံးပြု၍ Python တွင် binomial ဖြန့်ဖြူးမှုကို သင်မြင်ယောင်နိုင်သည်-

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

လက်ဖက်ရည်