Binomial ဖြန့်ဖြူးခြင်း၏ ပုံသဏ္ဍာန်ကို နားလည်ခြင်း။

binomial distribution သည် n binomial စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများ ရရှိရန် ဖြစ်နိုင်ခြေကို ဖော်ပြသည်။

ကျပန်း variable X သည် binomial distribution ကို လိုက်နာပါ က ၊ X = k အောင်မြင်မှု ဖြစ်နိုင်ခြေကို အောက်ပါဖော်မြူလာဖြင့် ရှာတွေ့နိုင်သည်-

P(X=k) = _n C _k * p ^k * (1-p) ^nk

ရွှေ-

• n: စမ်းသပ်မှုအရေအတွက်
• k: အောင်မြင်မှုအရေအတွက်
• p- ပေးထားသော စမ်းသပ်မှုတစ်ခုတွင် အောင်မြင်နိုင်ခြေ
• _n C _k : n စမ်းသပ်မှုများတွင် k အောင်မြင်မှုများရရှိရန် နည်းလမ်းများ

အောက်ဖော်ပြပါ အခြေအနေ နှစ်ခုအနက် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော အခြေအနေများ ဖြစ်ပေါ်သောအခါတွင် binomial ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုသည် ခေါင်းလောင်းပုံသဏ္ဍာန် ဖြစ်တတ်သည်-

1. နမူနာအရွယ်အစား (n) သည် ကြီးမားသည်။

2. ပေးထားသောစမ်းသပ်မှုတစ်ခုအတွက် အောင်မြင်နိုင်ခြေ (p) သည် 0.5 နီးပါးဖြစ်သည်။

သို့သော်၊ ဤအခြေအနေနှစ်ခုစလုံးမဖြစ်ပေါ်သောအခါတွင် binomial ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် လှည့်စားခံရတတ်သည်။ ယင်းကို သရုပ်ဖော်ရန် အောက်ပါ ဥပမာများကို သုံးသပ်ကြည့်ပါ။

ဥပမာ 1- နမူနာအရွယ်အစား (n) သည် ကြီးမားသည်။

အောက်ပါဂရပ်သည် n = 200 နှင့် p = 0.5 တွင်ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုကိုပြသသည်။

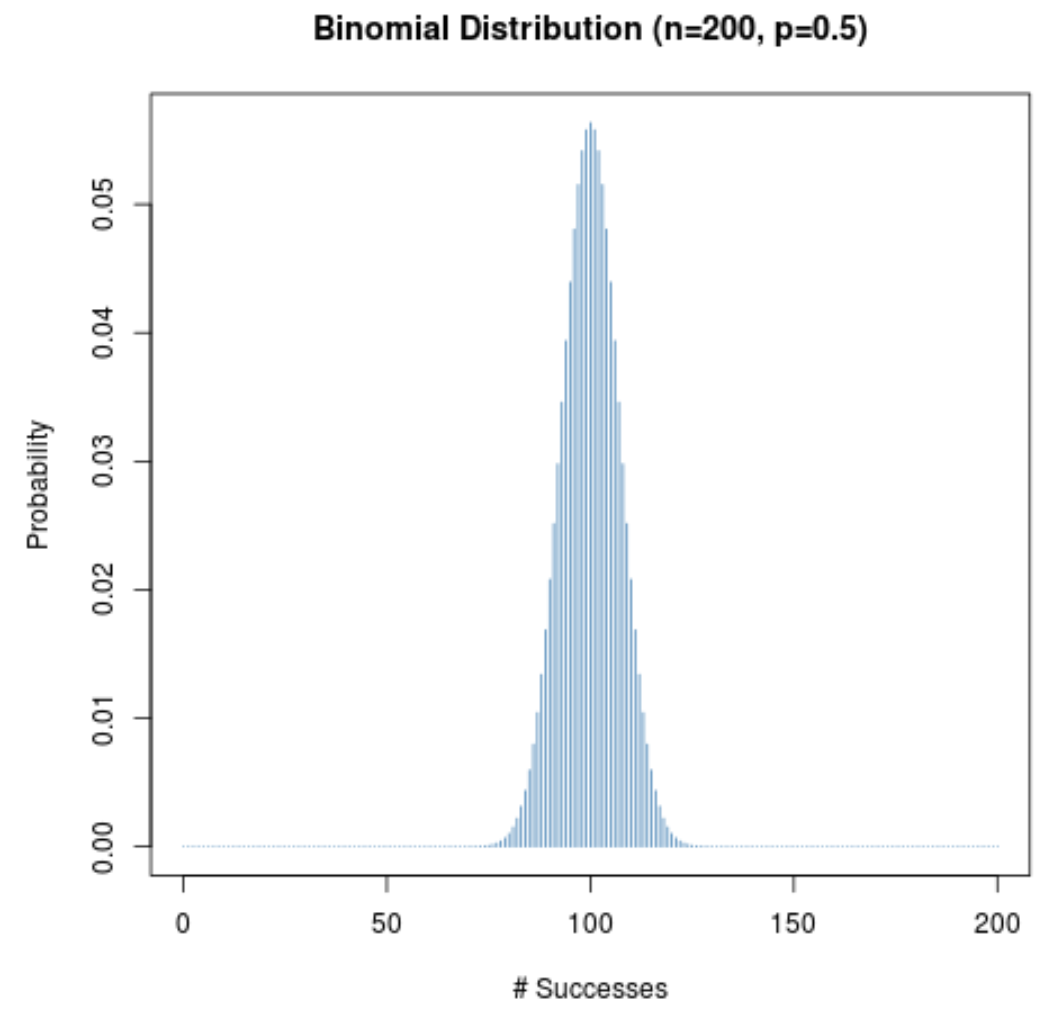
x-axis သည် စမ်းသပ်မှုပေါင်း 200 ကျော် အောင်မြင်မှု အရေအတွက်ကို ပြသပြီး y-axis သည် ထိုအောင်မြင်မှု အရေအတွက်၏ ဖြစ်နိုင်ခြေကို ပြသသည်။

(1) နမူနာအရွယ်အစားသည် ကြီးမားပြီး (2) စမ်းသပ်မှုတစ်ခုအတွက် အောင်မြင်နိုင်ခြေသည် 0.5 နီးပါးဖြစ်သောကြောင့်၊ ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် ခေါင်းလောင်းပုံသဏ္ဍာန်ဖြစ်သည်။

ပေးထားသော စမ်းသပ်မှု (p) အတွက် အောင်မြင်နိုင်ခြေသည် 0.5 နှင့် မနီးစပ်သော်လည်း၊ နမူနာ အရွယ်အစား (n) ကြီးသရွေ့ ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုသည် ခေါင်းလောင်းပုံသဏ္ဍာန် ရှိနေမည်ဖြစ်သည်။ ယင်းကို သရုပ်ဖော်ရန် p = 0.2 နှင့် p = 0.8 ဖြစ်သောအခါ အောက်ပါ မြင်ကွင်းနှစ်ခုကို သုံးသပ်ကြည့်ပါ။

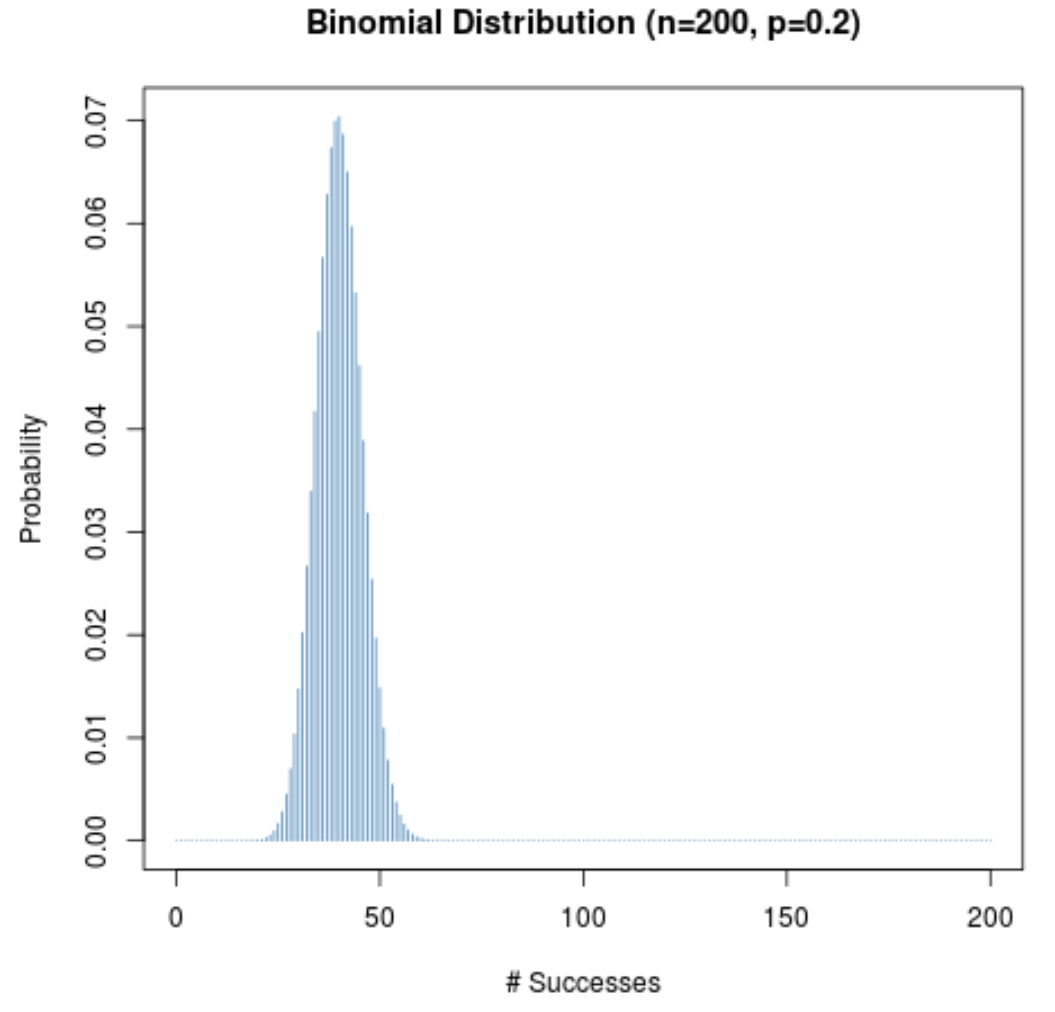
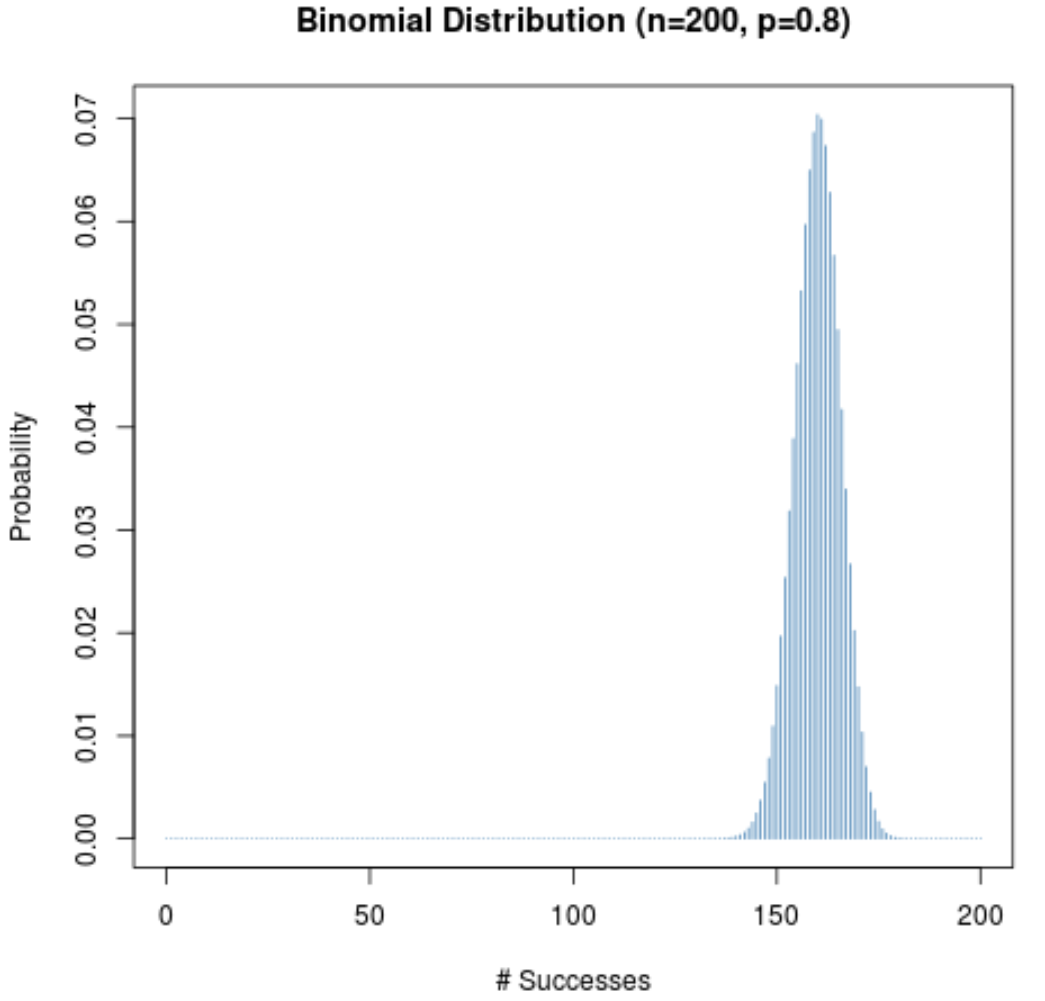
ဖြစ်ရပ်နှစ်ခုစလုံးတွင် ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုသည် ခေါင်းလောင်းပုံသဏ္ဍာန်ကို သတိပြုပါ။

ဥပမာ 2- အောင်မြင်မှု၏ဖြစ်နိုင်ခြေ (p) သည် 0.5 နီးပါးဖြစ်သည်။

အောက်ပါဂရပ်သည် n = 10 နှင့် p = 0.4 တွင်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုကိုပြသသည်။

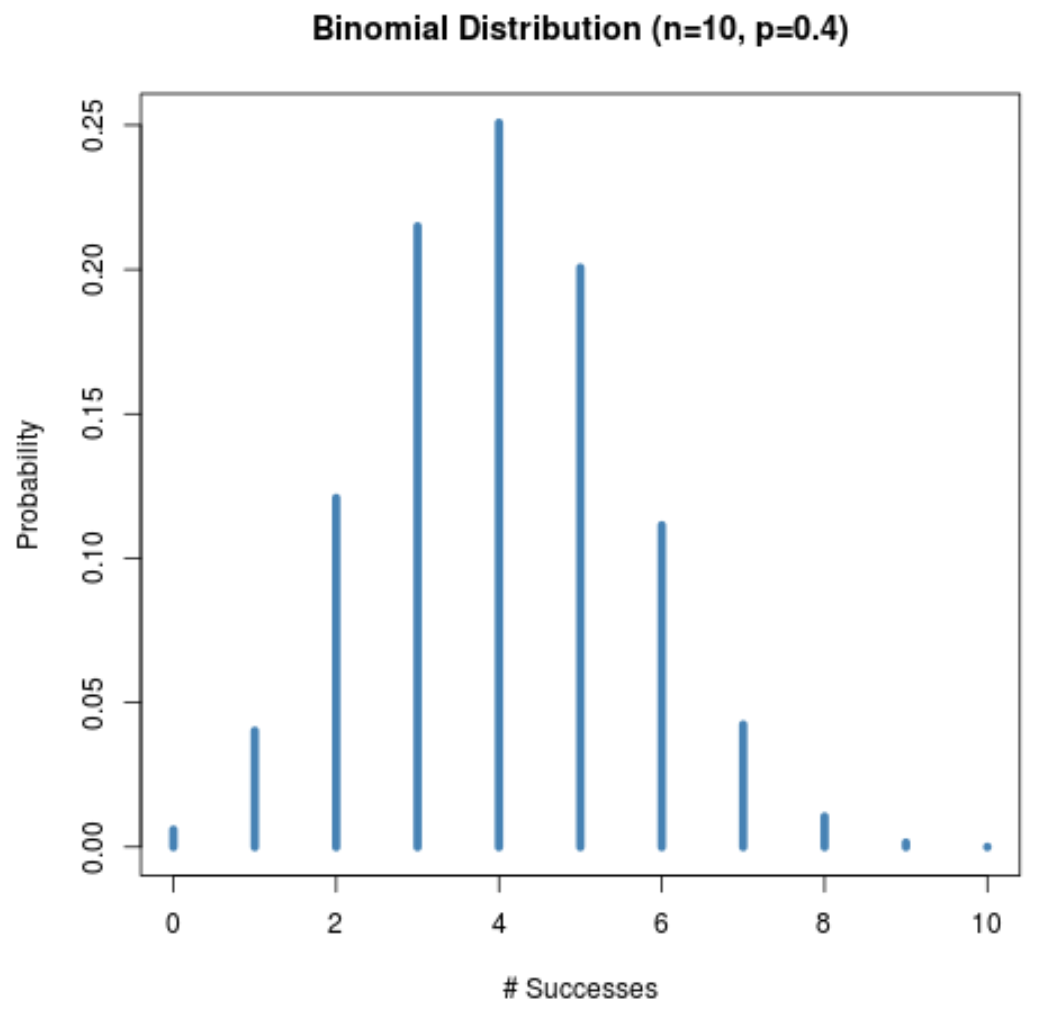
နမူနာအရွယ်အစား (n = 10) သည် သေးငယ်သော်လည်း၊ ပေးထားသော စမ်းသပ်မှုတစ်ခုအတွက် အောင်မြင်နိုင်ခြေ (p = 0.4) သည် 0.5 နီးပါးဖြစ်သောကြောင့် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် ခေါင်းလောင်းပုံသဏ္ဌာန်ရှိနေပါသည်။

ဥပမာ 3- binomial ခွဲဝေမှုများကို လှည့်ပတ်ထားသည်။

(1) နမူနာအရွယ်အစားသည် ကြီးမားသည်မဟုတ်သလို (2) ပေးထားသောစမ်းသပ်မှုတစ်ခု၏အောင်မြင်နိုင်ခြေသည် 0.5 နှင့်နီးစပ်သောအခါ၊ binomial ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် ဘယ် သို့မဟုတ် ညာဘက်သို့ စောင်းသွားပါမည်။

ဥပမာအားဖြင့်၊ အောက်ပါဂရပ်သည် n = 20 နှင့် p = 0.1 တွင် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို ပြသသည်။

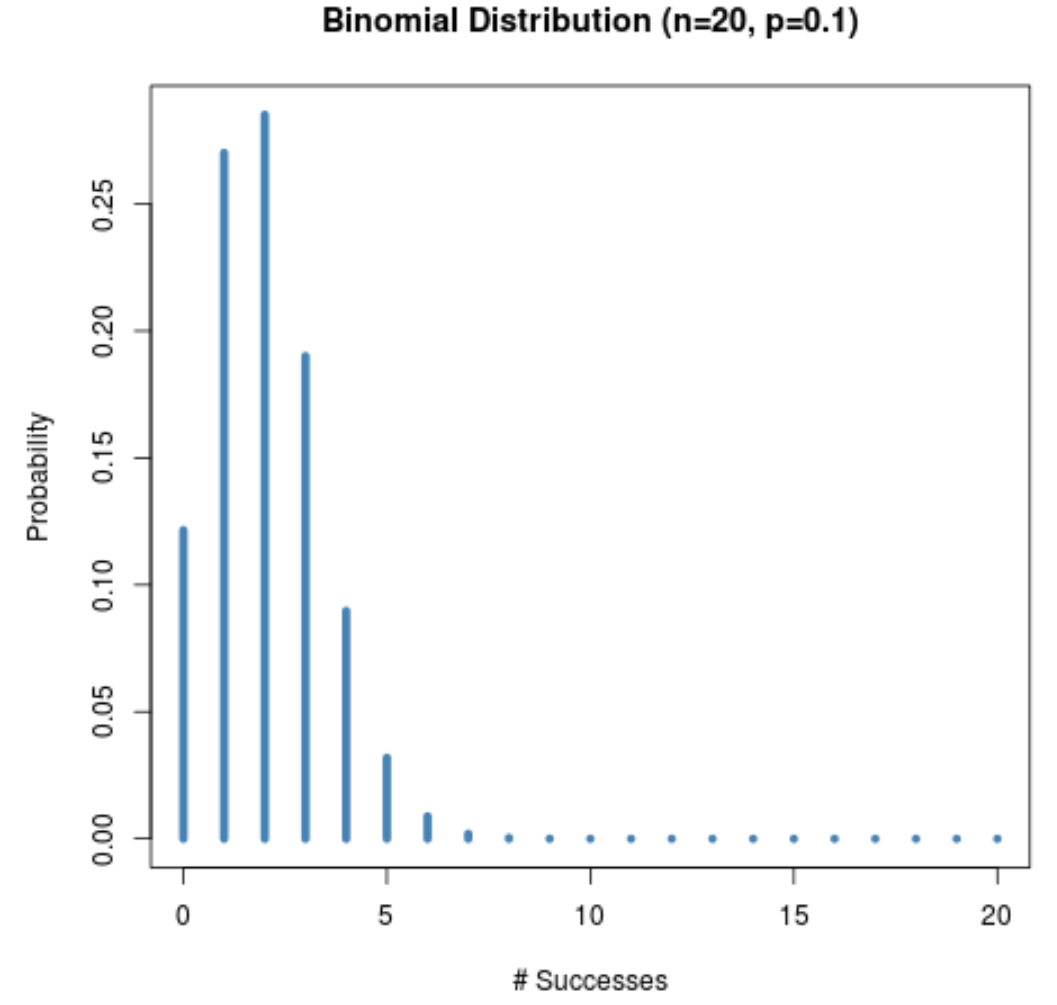
ဖြန့်ဖြူးမှုကို ညာဘက်သို့ မည်ကဲ့သို့ လွှဲထားသည်ကို သတိပြုပါ။

အောက်ဖော်ပြပါဂရပ်သည် n = 20 နှင့် p = 0.9 တွင်ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုကိုပြသသည်။

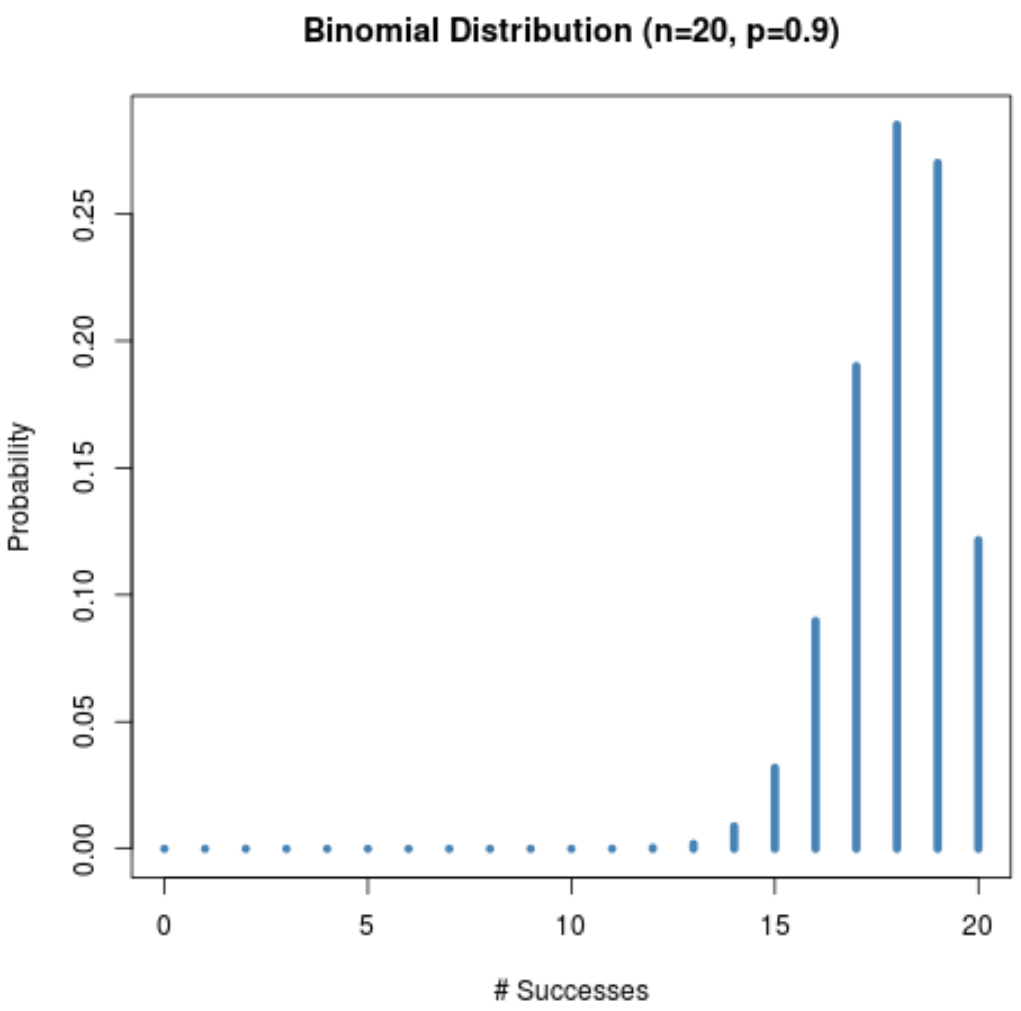
ဖြန့်ဖြူးမှုအား ဘယ်ဘက်သို့ စောင်းသွားသည်ကို သတိပြုပါ။

နောက်ဆုံးမှတ်စုများ

ဤဆောင်းပါးရှိ ဂရပ်ဖစ်တစ်ခုစီကို R စာရင်းအင်းပရိုဂရမ်းမင်းဘာသာစကားဖြင့် ဖန်တီးထားသည်။ ဤသင်ခန်းစာကို အသုံးပြု၍ R တွင် သင့်ကိုယ်ပိုင် binomial ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုများကို မည်သို့စီစဉ်ရမည်ကို လေ့လာပါ။