လက်တွေ့ဘဝတွင် bivariate data နမူနာ ၅ ခု

Bivariate data သည် variable နှစ်ခုတိတိပါဝင်သော ဒေတာအစုံကို ရည်ညွှန်းသည်။

ဤဒေတာအမျိုးအစားသည် လက်တွေ့ကမ္ဘာအခြေအနေများတွင် အချိန်တိုင်းပေါ်လာပြီး ဤဒေတာအမျိုးအစားကိုခွဲခြမ်းစိတ်ဖြာရန် အောက်ပါနည်းလမ်းများကို ကျွန်ုပ်တို့အသုံးပြုလေ့ရှိသည်-

• တိမ်တွေညွှန်တယ်။
• ဆက်စပ်ကိန်းများ
• ရိုးရှင်းသော linear ဆုတ်ယုတ်မှု

အောက်ပါဥပမာများသည် လက်တွေ့ဘဝတွင် bivariate data များပေါ်လာသည့် မတူညီသောအခြေအနေများကိုပြသသည်။

ဥပမာ 1- စီးပွားရေး

ကုမ္ပဏီများသည် ကြော်ငြာခနှင့် စုစုပေါင်းဝင်ငွေအတွက် အသုံးပြုသည့် စုစုပေါင်းငွေအပေါ် ကွဲပြားသော အချက်အလက်များကို စုဆောင်းလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ ကုမ္ပဏီတစ်ခုသည် 12 ဆက်တိုက် အရောင်းသုံးလပတ်များအတွက် အောက်ပါဒေတာများကို စုဆောင်းနိုင်သည်-

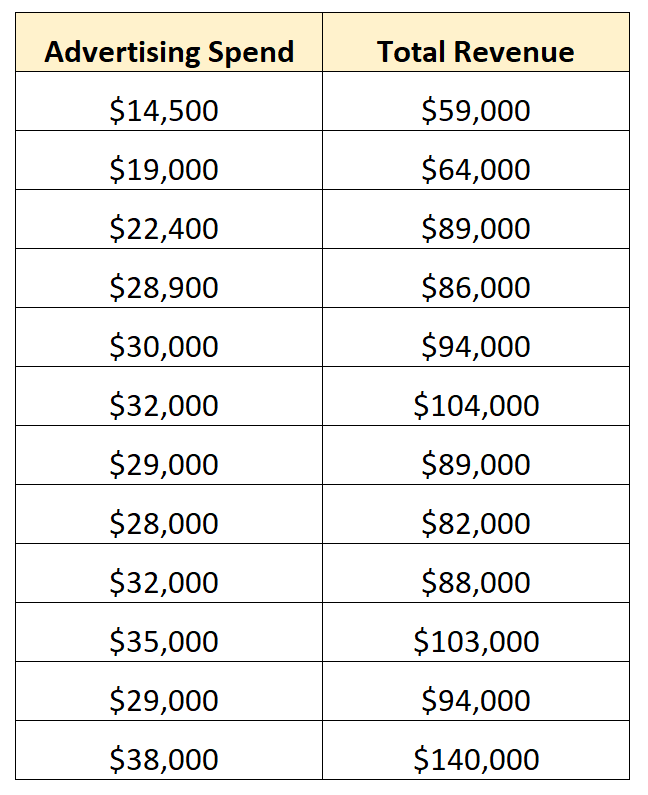
၎င်းတွင် ကြော်ငြာအသုံးစရိတ်နှင့် စုစုပေါင်းရငွေ အတိအကျတွင် ကိန်းရှင်နှစ်ခုတွင် အချက်အလက်ပါဝင်သောကြောင့် ၎င်းတွင် bivariate data ၏ ဥပမာတစ်ခုဖြစ်သည်။

ကုမ္ပဏီသည် ဤဒေတာအတွဲအတွက် ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို အံဝင်ခွင်ကျဖြစ်အောင် ဆုံးဖြတ်ပြီး အောက်ပါ တပ်ဆင်ထားသော မော်ဒယ်ကို ရှာဖွေနိုင်သည်-

စုစုပေါင်းဝင်ငွေ = 14,942.75 + 2.70* (ကြော်ငြာစရိတ်)

၎င်းသည် ကြော်ငြာအတွက်အသုံးပြုသည့် နောက်ထပ်ဒေါ်လာတိုင်းအတွက် စုစုပေါင်းဝင်ငွေသည် ပျမ်းမျှ $2.70 တိုးလာကြောင်း ကုမ္ပဏီကိုပြောပြသည်။

ဥပမာ 2- ဆေးဘက်ဆိုင်ရာ

ကျန်းမာရေးဆိုင်ရာ ကိန်းရှင်များကြားတွင် ဆက်စပ်မှုကို ပိုမိုနားလည်ရန် ဆေးသုတေသီများသည် bivariate data များကို စုဆောင်းလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ သုတေသီတစ်ဦးသည် လူ 15 ဦးထံမှ အောက်ပါအသက်အရွယ်နှင့် ကျန်နှလုံးခုန်နှုန်းဒေတာကို စုဆောင်းနိုင်သည်-

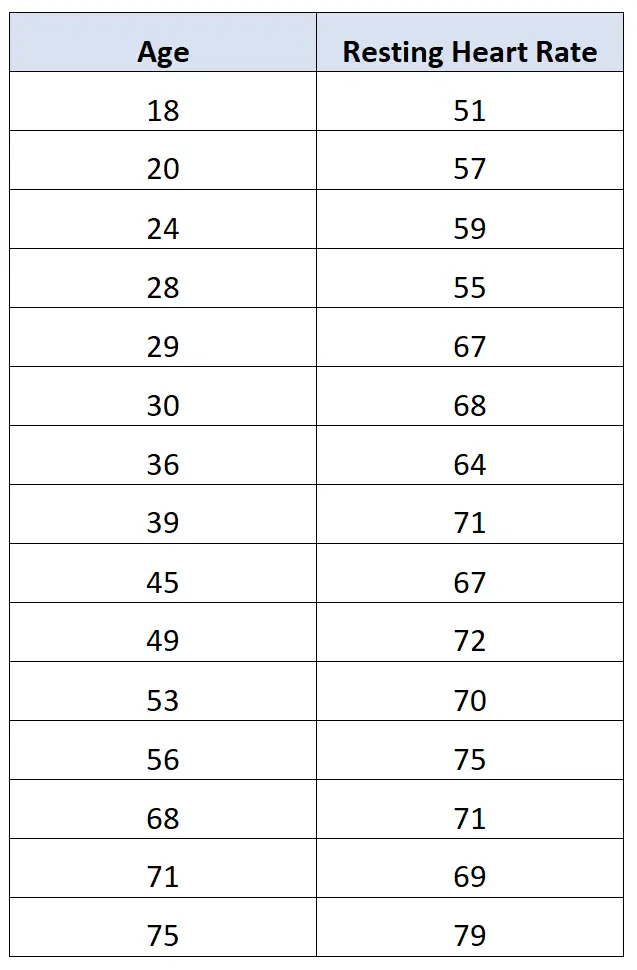
ထို့နောက် သုတေသီသည် ကိန်းရှင် နှစ်ခုကြား ဆက်စပ်မှုကို တွက်ချက်ပြီး 0.812 နှင့် ညီမျှကြောင်း တွေ့ရှိနိုင်သည်။

၎င်းသည် ကိန်းရှင်နှစ်ခုကြားတွင် ခိုင်မာသော အပြုသဘောဆက်စပ်ဆက်စပ်မှုရှိကြောင်းကို ညွှန်ပြသည်။ ဆိုလိုသည်မှာ အသက်ကြီးလာသည်နှင့်အမျှ ကျန်ရှိသော နှလုံးခုန်နှုန်းသည်လည်း တိုးမြင့်လာပါသည်။

ဆက်စပ်မှု- အဘယ်အရာကို “ခိုင်မာသော” ဆက်စပ်မှုဟု ယူဆသနည်း။

ဥပမာ 3- ပညာရှင်များ

သုတေသီများသည် ကောလိပ်ကျောင်းသား၏ စွမ်းဆောင်ရည်ကို ထိခိုက်စေသည့် ကိန်းရှင်များကို နားလည်ရန် ကွဲပြားသော အချက်အလက်များကို စုဆောင်းလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ သုတေသီတစ်ဦးသည် တစ်ပတ်လျှင် လေ့လာသည့် နာရီအရေအတွက်နှင့် အတန်းတစ်ခုရှိ ကျောင်းသားများအတွက် သက်ဆိုင်သည့် GPA အချက်အလက်များ စုဆောင်းနိုင်သည်-

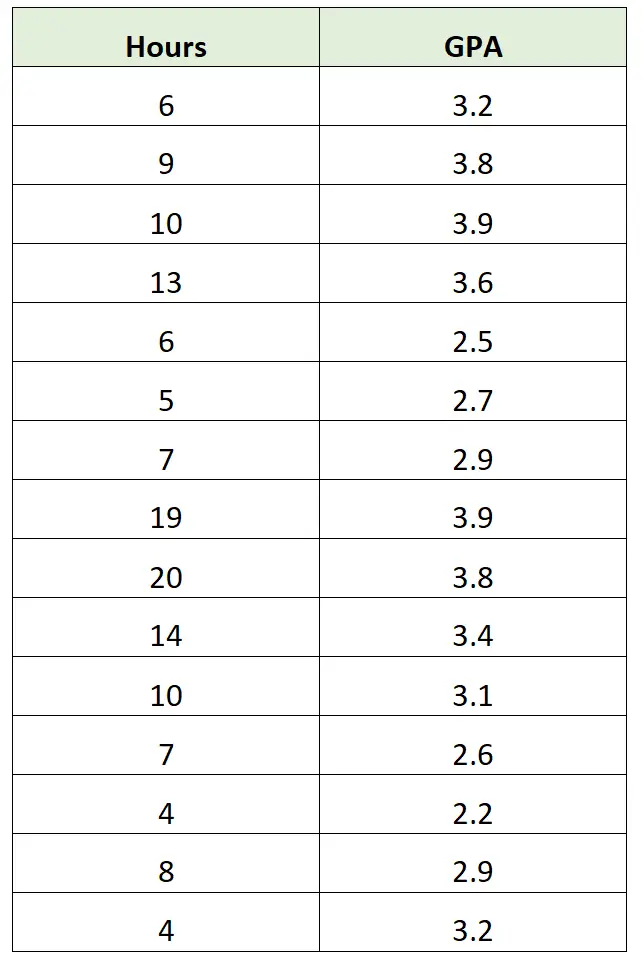
ထို့နောက် သူမသည် ဤကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို မြင်ယောင်နိုင်ရန် ရိုးရှင်းသော အပိုင်းအစတစ်ခုကို ဖန်တီးနိုင်သည်-

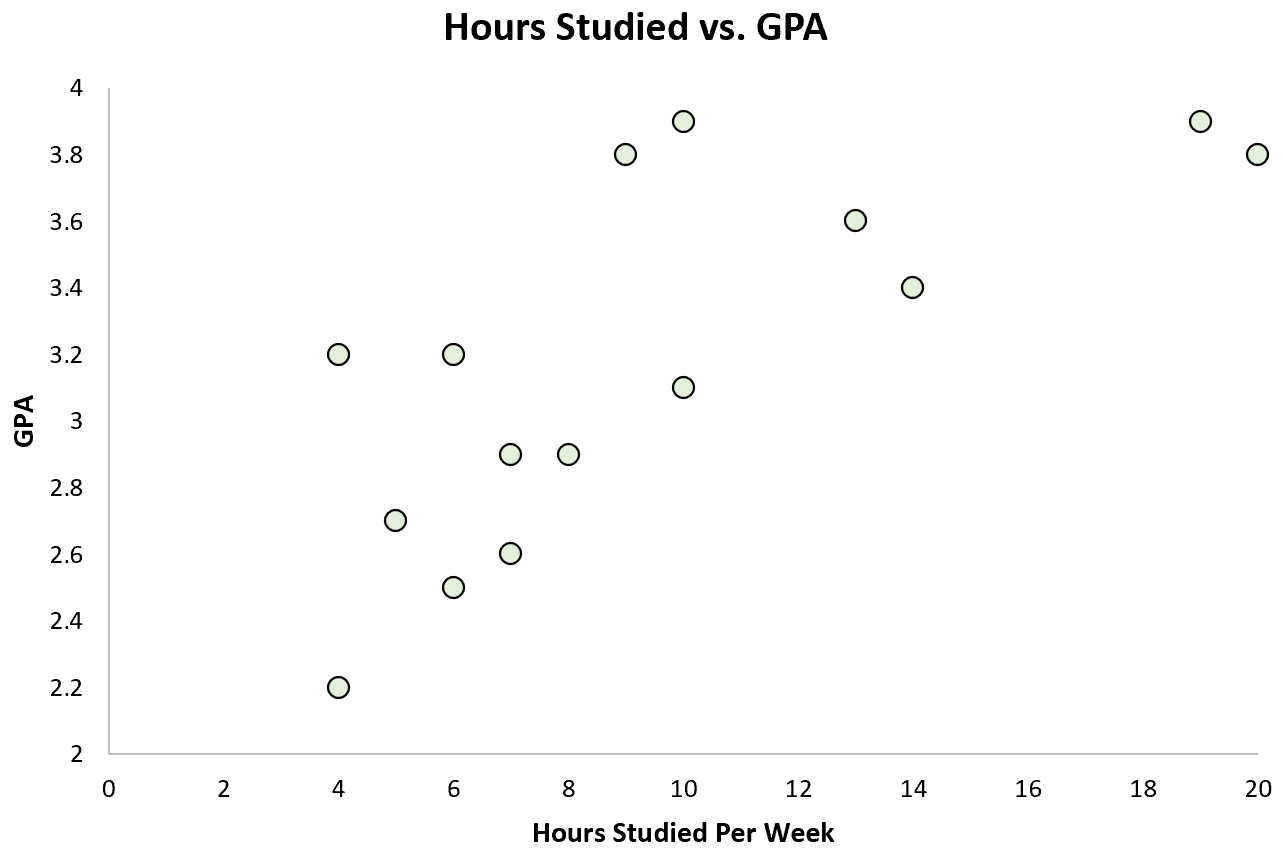
ကိန်းရှင်နှစ်ခုကြားတွင် အပြုသဘောဆောင်သော ဆက်စပ်မှုရှိကြောင်း ရှင်းရှင်းလင်းလင်းရှိပါသည်- တစ်ပတ်လျှင် လေ့လာသည့် နာရီအရေအတွက် တိုးလာသည်နှင့်အမျှ ကျောင်းသား၏ GPA သည်လည်း တိုးလာပါသည်။

ဥပမာ 4- စီးပွားရေး

ဘောဂဗေဒပညာရှင်များသည် လူမှုစီးပွားရေး ကိန်းရှင်နှစ်ခုကြား ဆက်စပ်မှုကို နားလည်ရန် ကွဲပြားသော အချက်အလက်များကို စုဆောင်းလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ ဘောဂဗေဒပညာရှင်တစ်ဦးသည် အချို့သောမြို့တစ်မြို့ရှိ လူတစ်ဦးချင်းစီ၏ စုစုပေါင်းနှစ်စဉ်ဝင်ငွေနှင့် ကျောင်းတက်သည့်နှစ်များဆိုင်ရာ အချက်အလက်များကို စုဆောင်းနိုင်သည်-

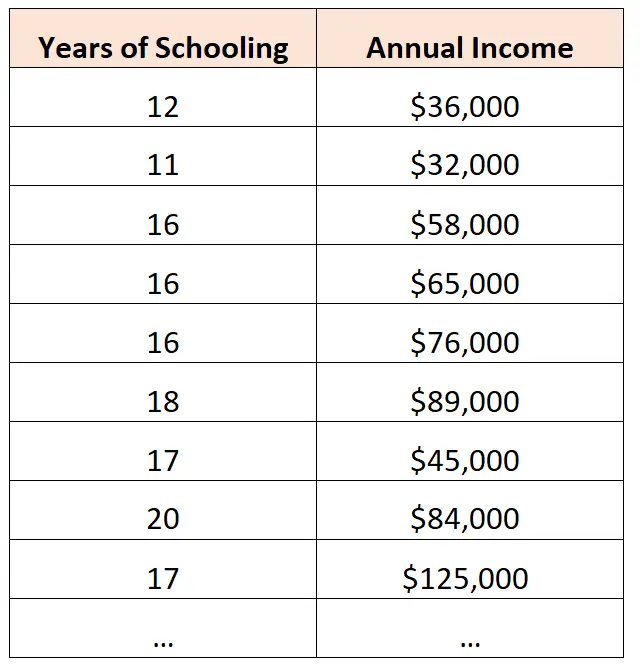
ထို့နောက် အောက်ပါရိုးရှင်းသော linear regression model ကို လိုက်လျောညီထွေဖြစ်အောင် ဆုံးဖြတ်နိုင်သည်-

တစ်နှစ်ဝင်ငွေ = -45,353 + 7,120*(ကျောင်းတက်နှစ်များ)

၎င်းသည် နောက်ထပ်ကျောင်းတက်သည့်နှစ်တိုင်းအတွက် နှစ်စဉ်ဝင်ငွေ ပျမ်းမျှ $7,120 တိုးလာသည်ဟု စီးပွားရေးပညာရှင်အား ပြောပြသည်။

ဥပမာ 5- ဇီဝဗေဒ

ဇီဝဗေဒပညာရှင်များသည် အပင်များ သို့မဟုတ် တိရိစ္ဆာန်များကြားတွင် ကိန်းရှင်နှစ်ခုသည် မည်သို့ဆက်စပ်ကြောင်း နားလည်ရန် bivariate data များကို စုဆောင်းလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ ဇီဝဗေဒပညာရှင်သည် မတူညီသော ဒေသအသီးသီးရှိ စုစုပေါင်းမိုးရွာသွန်းမှုနှင့် အပင်အရေအတွက် စုစုပေါင်းဆိုင်ရာ အချက်အလက်များကို စုဆောင်းနိုင်သည်-

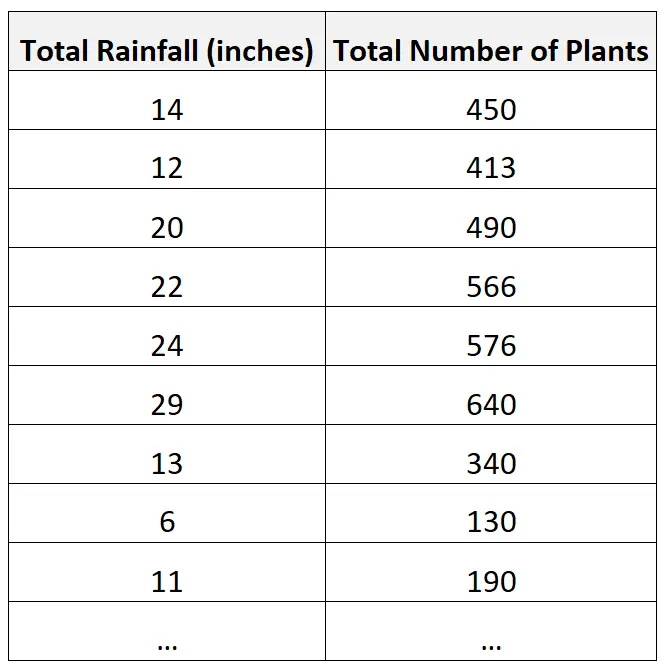
ထို့နောက် ဇီဝဗေဒပညာရှင်သည် ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို တွက်ချက်ကာ 0.926 နှင့် ညီမျှကြောင်း တွေ့ရှိနိုင်သည်။

၎င်းသည် ကိန်းရှင်နှစ်ခုကြားတွင် ခိုင်မာသော အပြုသဘောဆက်စပ်ဆက်စပ်မှုရှိကြောင်းကို ညွှန်ပြသည်။

ဆိုလိုသည်မှာ၊ မြင့်မားသောမိုးရွာသွန်းမှုသည် ဒေသတစ်ခုတွင် အပင်အရေအတွက် တိုးလာခြင်းနှင့် နီးကပ်စွာဆက်စပ်နေသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် bivariate data နှင့် ခွဲခြမ်းစိတ်ဖြာနည်းနှင့်ပတ်သက်သော နောက်ထပ်အချက်အလက်များကို ပေးပါသည်။

Bivariate ခွဲခြမ်းစိတ်ဖြာခြင်းအတွက် နိဒါန်း
Univariate Analysis ကို နိဒါန်း
Pearson Correlation Coefficient ကို နိဒါန်း
Simple Linear Regression နိဒါန်း