R တွင် box-cox အသွင်ပြောင်းနည်း (ဥပမာများနှင့်အတူ)

box-cox အသွင်ပြောင်းခြင်းသည် ပုံမှန်မဟုတ်သော ဖြန့်ဝေထားသောဒေတာအစုံကို ပိုမို သာမာန်ဖြန့်ဝေမှု အစုအဖြစ်သို့ ပြောင်းလဲရန်အတွက် အသုံးများသောနည်းလမ်းဖြစ်သည်။

ဤနည်းလမ်း၏နောက်ကွယ်တွင် အခြေခံအယူအဆမှာ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ ပြောင်းလဲထားသောဒေတာသည် ပုံမှန်ဖြန့်ဝေမှုအတိုင်း ဖြစ်နိုင်ချေနီးစပ်သည့် λ တန်ဖိုးတစ်ခုကို ရှာဖွေရန်ဖြစ်သည်-

• y(λ) = (y ^λ – 1) / λ ဆိုလျှင် y ≠ 0
• y(λ) = log(y) ဆိုရင် y = 0

MASS() စာကြည့်တိုက်မှ boxcox() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ R တွင် box-cox အသွင်ပြောင်းခြင်းကို လုပ်ဆောင်နိုင်သည်။ အောက်ဖော်ပြပါ ဥပမာသည် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

Box-Cox အသွင်ပြောင်းမှု ဖွံ့ဖြိုးတိုးတက်မှု၏ ကောင်းမွန်သော အကျဉ်းချုပ်အတွက် Connecticut တက္ကသိုလ်မှ ဤဆောင်းပါးကို ကိုးကားပါ။

ဥပမာ- R in Box-Cox အသွင်ပြောင်းခြင်း

အောက်ပါကုဒ်သည် ဒေတာအတွဲတစ်ခုနှင့် မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို မည်ကဲ့သို့ အံဝင်ခွင်ကျလုပ်ရမည်ကို ပြသသည်၊ ထို့နောက် တုံ့ပြန်မှုကိန်းရှင်ကို ပြောင်းလဲပြီး မော်ဒယ်အသစ်နှင့် အံဝင်ခွင်ကျဖြစ်စေရန် အကောင်းဆုံးသော lambda တစ်ခုကို ရှာဖွေရန် boxcox() လုပ်ဆောင်ချက်ကို အသုံးပြုပါ။

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

အကောင်းဆုံး lambda သည် -0.4242424 ဖြစ်သွားသည်။ ထို့ကြောင့်၊ ဆုတ်ယုတ်မှုပုံစံအသစ်သည် မူလတုံ့ပြန်မှုကိန်းရှင် y ကို ကိန်းရှင် y = (y ^-0.4242424 – 1) / -0.4242424 ဖြင့် အစားထိုးခဲ့သည်။

အောက်ဖော်ပြပါကုဒ်သည် ဆုတ်ယုတ်မှုပုံစံနှစ်ခုကြားရှိ အကြွင်းအကျန်များကို မြင်သာစေရန် R တွင် QQ အကွက် နှစ်ခုကို ဖန်တီးနည်းကို ပြသသည်-

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

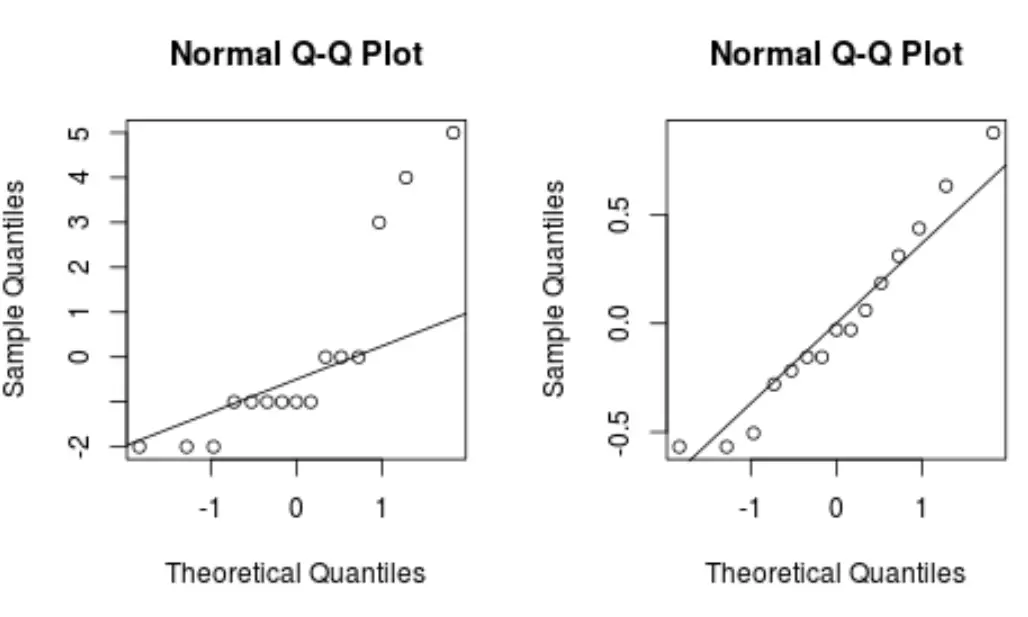
ယေဘူယျအားဖြင့်၊ ဒေတာအမှတ်များသည် QQ ကွက်ကွက်တစ်ခုရှိ ဖြောင့်ထောင့်ဖြတ်မျဉ်းတစ်လျှောက်တွင် ရှိနေပါက၊ ဒေတာအစုံသည် ပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်နိုင်သည်။

box-cox အသွင်ပြောင်းမော်ဒယ်သည် မူရင်းဆုတ်ယုတ်မှုမော်ဒယ်ထက် များစွာဖြောင့်တန်းသော QQ ကွက်ကွက်ကို မည်သို့ထုတ်လုပ်သည်ကို သတိပြုပါ။

၎င်းသည် အကွက်-ကော့စ်အသွင်ပြောင်းထားသော မော်ဒယ်၏ အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေသည်၊ ၎င်းသည် linear regression ၏ ယူဆချက် တစ်ခုအား ကျေနပ်စေသည်။

ထပ်လောင်းအရင်းအမြစ်များ

R (Log၊ Square Root၊ Cube Root) ဖြင့် Data ကိုဘယ်လိုပြောင်းမလဲ
R တွင် QQ ကွက်ကွက်တစ်ခုကို ဖန်တီးပြီး အဓိပ္ပာယ်ဖွင့်နည်း
R တွင်ပုံမှန်ဖြစ်ရန်အတွက် Shapiro-Wilk စမ်းသပ်နည်း