ပုံမှန် cdf ကို r တွင်အသုံးပြုနည်း (ဥပမာများနှင့်အတူ)

R တွင် ပုံမှန် CDF (စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်) ဖြင့် အလုပ်လုပ်ရန် အောက်ပါနည်းလမ်းများကို သင်အသုံးပြုနိုင်ပါသည်။

နည်းလမ်း 1- ပုံမှန် CDF ဖြစ်နိုင်ခြေများကို တွက်ချက်ပါ။

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

#calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

နည်းလမ်း 2- ပုံမှန် CDF ကိုဆွဲပါ။

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ")

အောက်ဖော်ပြပါ ဥပမာများသည် ဤနည်းလမ်းများကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

ဥပမာ 1- ပုံမှန် CDF ဖြစ်နိုင်ခြေကို တွက်ချက်ပါ။

အောက်ဖော်ပြပါ ကုဒ်သည် ကျပန်း ကိန်းရှင်သည် စံပုံမှန် ဖြန့်ဝေမှုတစ်ခုတွင် 1.96 ထက်နည်းသော တန်ဖိုးကို ယူဆောင်သည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ပုံကို ပြသည်-

 #calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)

[1] 0.9750021

ကျပန်းကိန်းရှင်တစ်ခုသည် ပုံမှန်ပုံမှန်ဖြန့်ဝေမှုတစ်ခုတွင် 1.96 ထက်နည်းသောတန်ဖိုးကိုယူသည့်ဖြစ်နိုင်ခြေမှာ 0.975 ဖြစ်သည်။

low.tail argument ကို အသုံးပြု၍ ကျပန်း variable သည် 1.96 ထက် ကြီးသောတန်ဖိုးကို ယူသည်ဟူသော ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်-

 #calculate probability that random value is greater than 1.96 in normal CDF
pnorm(1.96, lower.tail = FALSE )

[1] 0.0249979

ကျပန်းကိန်းရှင်တစ်ခုသည် စံပုံမှန်ဖြန့်ဝေမှုတစ်ခုတွင် တန်ဖိုးနှစ်ခုကြားရှိ တန်ဖိုးတစ်ခုယူဆောင်နိုင်သည့်ဖြစ်နိုင်ခြေကို ရှာဖွေရန် အောက်ပါ syntax ကို အသုံးပြုနိုင်သည်။

 #calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)

[1] 0.9500042

စံပုံမှန်ဖြန့်ဝေမှုတစ်ခုတွင် -1.96 နှင့် 1.96 ကြားတန်ဖိုးတစ်ခုကျပန်းကိန်းရှင်တစ်ခုယူသည့်ဖြစ်နိုင်ခြေမှာ 0.95 ဖြစ်သည်။

ဥပမာ 2- ပုံမှန် CDF ကိုဆွဲခြင်း။

အောက်ပါ ကုဒ်သည် သာမန် CDF ကို မည်သို့ဆွဲရမည်ကို ပြသသည် ။

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=" l ") 

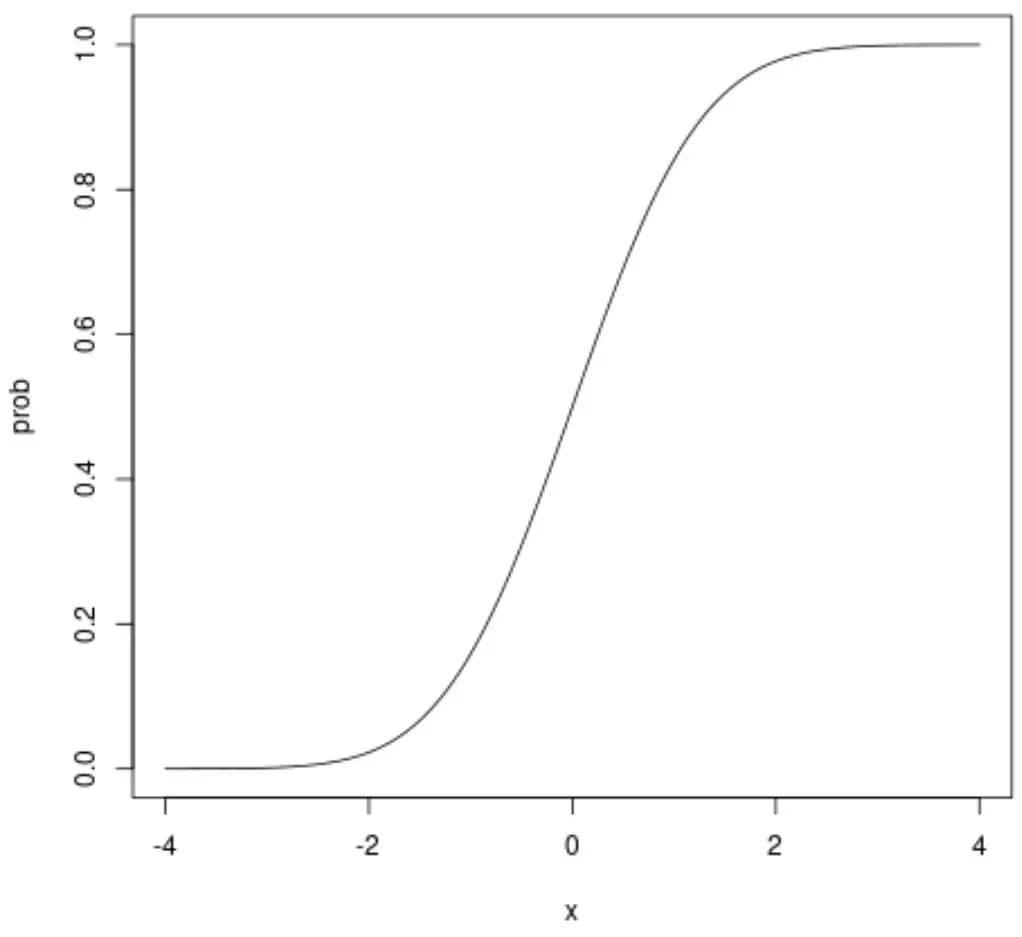
x-axis သည် စံပုံမှန်ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သော ကျပန်း variable ၏တန်ဖိုးများကိုပြသပြီး y-axis သည် x-axis တွင်ပြသထားသည့်တန်ဖိုးထက်နည်းသောတန်ဖိုးထက်ကျပန်းကိန်းရှင်တစ်ခုယူနိုင်ခြေကိုပြသသည်။

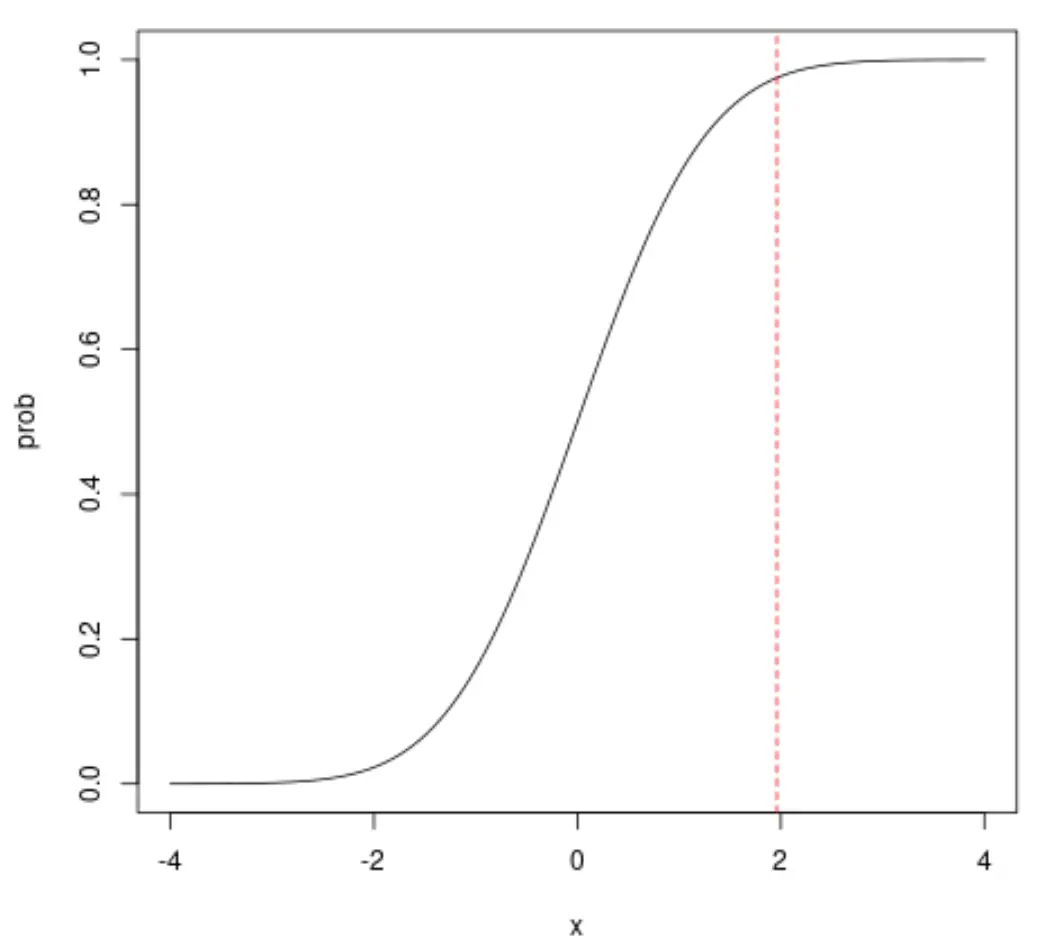
ဥပမာ၊ x = 1.96 ကိုကြည့်လျှင် x သည် 1.96 အောက်ဖြစ်နိုင်ခြေသည် ခန့်မှန်းခြေအားဖြင့် 0.975 ဖြစ်သည်ကို တွေ့ရပါမည်။

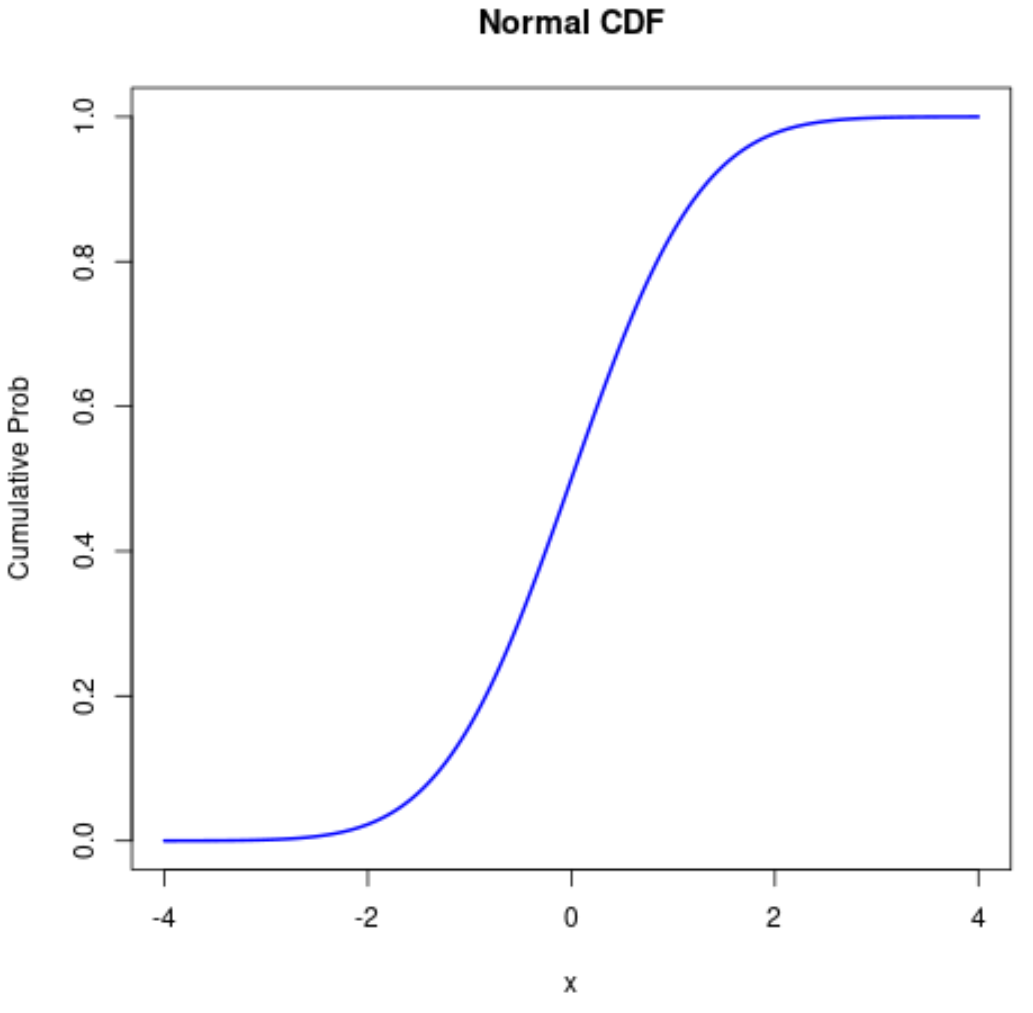
ပုံမှန် CDF ဇာတ်ကွက်၏ အလှတရားကိုလည်း ပြောင်းလဲနိုင်သည်ကို သတိပြုပါ။

 #define sequence of x-values
x <- seq(-4, 4, .01)

#calculate normal CDF probabilities
prob <- pnorm(x)
 
#normal plot CDF
plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ') 

ဆက်စပ်- R တွင် seq လုပ်ဆောင်ချက်ကို အသုံးပြုနည်း

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အခြားသော ဘုံလုပ်ဆောင်ချက်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

R ဖြင့် ပုံမှန်ဖြန့်ဖြူးနည်း
R တွင် Z ရမှတ်များ တွက်နည်း
R တွင် dnorm၊ pnorm၊ qnorm နှင့် rnorm လမ်းညွှန်