Ti-84 ဂဏန်းတွက်စက်တွင် central limit theorem ကို ဘယ်လိုအသုံးချမလဲ။
လူဦးရေ ဖြန့်ဝေမှုသည် ပုံမှန်မဟုတ်သော်လည်း နမူနာအရွယ်အစား လုံလောက်စွာကြီးမားပါက နမူနာ၏နမူနာဖြန့်ဝေမှုသည် ပုံမှန်မဟုတ်ကြောင်း ဗဟိုကန့်သတ်သီအိုရီက ဖော်ပြသည်။
ဗဟိုကန့်သတ်သီအိုရီတွင်လည်း နမူနာဖြန့်ဝေမှုတွင် အောက်ပါဂုဏ်သတ္တိများ ပါလိမ့်မည်-
1. နမူနာဖြန့်ဝေမှု၏ပျမ်းမျှသည် လူဦးရေဖြန့်ဖြူးမှု၏ပျမ်းမျှနှင့် ညီမျှသည်-
x = µ
2. နမူနာ ဖြန့်ဝေမှု၏ စံသွေဖည်မှုသည် နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားထားသော လူဦးရေ စံသွေဖည်မှုနှင့် ညီမျှသည်-
s = σ / √n
TI-84 ဂဏန်းတွက်စက်ရှိ နမူနာဆိုလိုမှုနှင့် ပတ်သက်သည့် ဖြစ်နိုင်ခြေများကို ရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါ syntax ဖြင့် normalcdf() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။
normalcdf (lower value, upper value, x , s/√ n )
ရွှေ-
- x : နမူနာဆိုလိုသည်။
- s : နမူနာစံသွေဖည်
- n : နမူနာအရွယ်အစား
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် ဤလုပ်ဆောင်ချက်ကို ဝင်ရောက်အသုံးပြုရန်၊ 2nd ကိုနှိပ်ပြီး VARS ကိုနှိပ်ပြီးနောက် normalcdf သို့ scroll ( ပြီး ENTER နှိပ်ပါ။
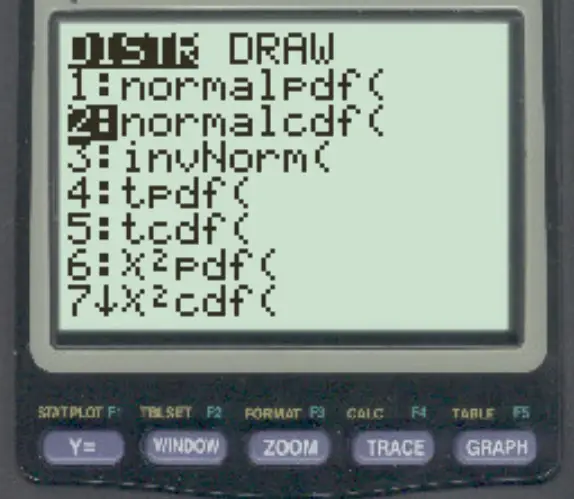
အောက်ဖော်ပြပါ ဥပမာများသည် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။
ဥပမာ 1- တန်ဖိုးနှစ်ခုကြားရှိ ဖြစ်နိုင်ခြေကို ရှာပါ။
ဖြန့်ဖြူးမှုတစ်ခုတွင် ပျမ်းမျှ 70 နှင့် စံသွေဖည်မှု 7 ရှိသည်။ ကျွန်ုပ်တို့သည် အရွယ်အစား n = 35 ၏ ကျပန်းနမူနာကို ရွေးချယ်ပါက၊ နမူနာဆိုလိုသည် 68 နှင့် 72 အကြား ဖြစ်နိုင်ခြေကို ရှာပါ။
TI-84 တွင် အောက်ပါ syntax ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။
normalcdf (68, 72, 70, 7/√ 35 )
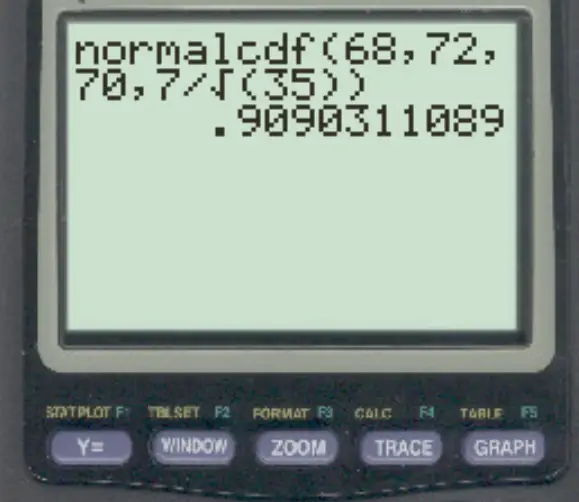
နမူနာဆိုလိုသည်မှာ 68 နှင့် 72 အကြားဖြစ်နိုင်ခြေမှာ 0.909 ဖြစ်သည်။
ဥပမာ 2- တန်ဖိုးထက် ဖြစ်နိုင်ခြေကို ရှာဖွေခြင်း။
ဖြန့်ဖြူးမှုတစ်ခုတွင် ပျမ်းမျှ 50 နှင့် စံသွေဖည်မှု 4 ရှိသည်။ ကျွန်ုပ်တို့သည် အရွယ်အစား n = 30 ၏ ကျပန်းနမူနာကို ရွေးချယ်ပါက၊ နမူနာဆိုလိုသည် 48 ထက် ပိုများသည်ဟု ဖြစ်နိုင်ခြေကို ရှာပါ။
TI-84 တွင် အောက်ပါ syntax ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။
normalcdf (48, E99, 50, 4/√ 30 )
မှတ်ချက်- 2 ကိုနှိပ်၍ ခလုတ်ကို နှိပ်ခြင်းဖြင့် “ E” သင်္ကေတကို သင်ဝင်ရောက်နိုင်သည်။
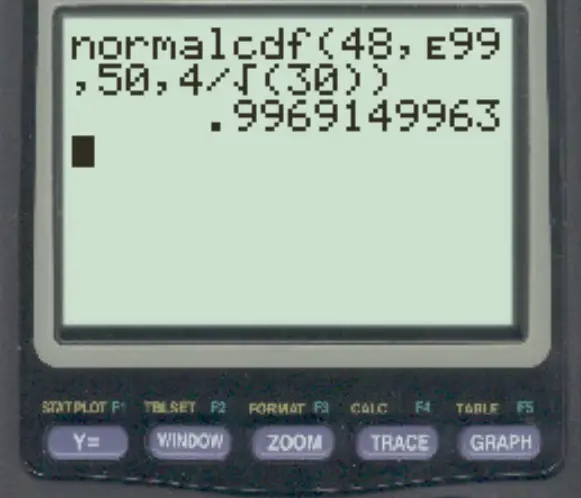
နမူနာဆိုလိုရင်းမှာ 48 ထက်များသော ဖြစ်နိုင်ခြေမှာ 0.9969 ဖြစ်သည်။
ဥပမာ 3- တန်ဖိုးတစ်ခုထက်နည်းသော ဖြစ်နိုင်ခြေကို ရှာဖွေခြင်း။
ဖြန့်ဖြူးမှုတစ်ခုတွင် ပျမ်းမျှ 20 နှင့် စံသွေဖည်မှု 3 ရှိသည်။ ကျွန်ုပ်တို့သည် အရွယ်အစား n = 40 ၏ ကျပန်းနမူနာကို ရွေးချယ်ပါက၊ နမူနာဆိုလိုသည် 19 ထက်နည်းသော ဖြစ်နိုင်ခြေကို ရှာပါ။
TI-84 တွင် အောက်ပါ syntax ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။
normalcdf (-E99, 19, 20, 3/√ 40 )
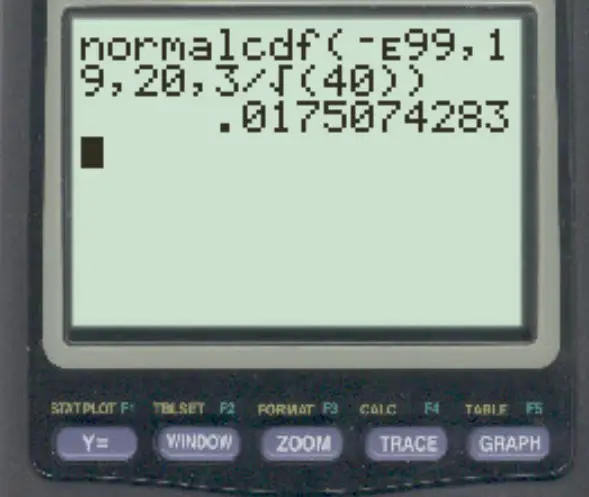
နမူနာဆိုလိုရင်းမှာ 19 ထက်နည်းသော ဖြစ်နိုင်ခြေမှာ 0.0175 ဖြစ်သည်။
ထပ်လောင်းအရင်းအမြစ်များ
Central Limit Theorem နိဒါန်း
Central Limit Theorem ဂဏန်းတွက်စက်
Excel တွင် Central Limit Theorem ကို ဘယ်လိုအသုံးချမလဲ။
ဗဟိုကန့်သတ်သီအိုရီ- ပြည့်စုံရမည့် အခြေအနေလေးခု