Chebyshev ၏သီအိုရီ
ဤဆောင်းပါးတွင် Chebyshev ၏သီအိုရီသည် မည်သည်ကို ရှင်းပြထားသည်။ ဤနေရာတွင် Chebyshev သီအိုရီ ဖော်မြူလာ၊ ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းနှင့် ထို့အပြင် အွန်လိုင်း Chebyshev သီအိုရီဂဏန်းတွက်စက်ကို သင်တွေ့လိမ့်မည်။ နောက်ဆုံးတွင်၊ ၎င်းသည် Chebyshev ၏သီအိုရီနှင့် empirical rule အကြားခြားနားချက်ကိုပြသသည်။
Chebyshev ရဲ့ သီအိုရီဆိုတာ ဘာလဲ။
Chebyshev’s theorem သည် Chebyshev’s inequality ဟုလည်းသိကြသော ကိန်းဂဏန်းစည်းမျဉ်းတစ်ခုဖြစ်ပြီး ကျပန်းကိန်းရှင်တစ်ခု၏တန်ဖိုးသည် ၎င်း၏ပျမ်းမျှအကွာအဝေးအတွင်းတွင်ရှိနေသောဖြစ်နိုင်ခြေကိုတွက်ချက်ရန်အသုံးပြုသည့်ကိန်းဂဏန်းစည်းမျဉ်းတစ်ခုဖြစ်သည်။
တစ်နည်းဆိုရသော် ကိန်းဂဏန်းစာရင်းအင်းများတွင် Chebyshev ၏သီအိုရီကို ယုံကြည်မှုကြားကာလတစ်ခုအတွင်း တန်ဖိုးတစ်ခုရှိနိုင်ခြေကို ဆုံးဖြတ်ရန် အသုံးပြုသည်။
ထို့အပြင် Chebyshev ၏ သီအိုရီကို ကိန်းဂဏန်းများစွာ၏ ဥပဒေကဲ့သို့ အခြားသော ကိန်းဂဏန်းဆိုင်ရာ သီအိုရီများကို သက်သေပြရန်အတွက်လည်း အသုံးပြုပါသည်။
Chebyshev ၏ သီအိုရီကို ပြင်သစ်လူမျိုး Irénée-Jules Bienaymé မှ ပထမဆုံး ပုံဖော်ခဲ့သော်ငြား သီအိုရီကို 1867 ခုနှစ်တွင် ရုရှား Pafnuty Chebushev မှ အစပြုခဲ့ခြင်းကြောင့် သီအိုရီကို အမည်ပေးခဲ့ပါသည်။
Chebyshev ၏သီအိုရီ၏ဖော်မြူလာ
Chebyshev ၏သီအိုရီအရ k နှစ်ထပ်ကိန်းဖြင့် ပိုင်းခြားထားသော ပျမ်းမျှတန်ဖိုး မှ k စံသွေဖည်မှုဖြစ်နိုင်ခြေသည် k နှစ်ထပ်ကိန်းဖြင့် ပိုင်းခြားထားသော အချိုးတစ်ခုထက် ကြီးသည် သို့မဟုတ် ညီမျှသည်ဟု Chebyshev ၏သီအိုရီကဆိုသည်။
ထို့ကြောင့် Chebyshev ၏သီအိုရီအတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်။
![]()
ရွှေ
![]()
Random variable ၏တန်ဖိုး၊
![]()
variable ၏ ဂဏန်းသင်္ချာပျမ်းမျှ ၊
![]()
၎င်း၏ စံသွေဖည်မှု နှင့်
![]()
ဖြစ်နိုင်ခြေကို တွက်ချက်ရမည့် ပျမ်းမျှမှ စံသွေဖည်သော အရေအတွက်။
တွက်ချက်မှုလုပ်ဆောင်သော စံသွေဖည်အရေအတွက်သည် 1 ထက် ကြီးပါက သို့မဟုတ် တစ်နည်းအားဖြင့် k သည် 1 ထက် ပိုများပါက၊ ဤဖော်မြူလာကို သတိပြုပါ။
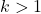 ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါအွန်လိုင်း Chebyshev Theorem ဂဏန်းတွက်စက်ကို သင်အသုံးပြုနိုင်ပါသည်။
ဖြစ်နိုင်ခြေကိုတွက်ချက်ရန် အောက်ပါအွန်လိုင်း Chebyshev Theorem ဂဏန်းတွက်စက်ကို သင်အသုံးပြုနိုင်ပါသည်။
Chebyshev ၏သီအိုရီဥပမာ
Chebyshev ၏ သီအိုရီ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာသည် မည်ကဲ့သို့ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်ပြီးသည်နှင့် ဤသဘောတရားကို ပိုမိုနားလည်ရန် ဤကိန်းဂဏန်းဆိုင်ရာ သီအိုရီ၏ ဖြေရှင်းပုံဥပမာတစ်ခုဖြစ်သည်။
- တက္ကသိုလ်၏ သင်ရိုးစာရင်းဇယားများတွင် ရရှိသောအဆင့်များကို ပျမ်းမျှ 65 နှင့် 10 စံသွေဖည်မှုဖြင့် ခွဲခြမ်းစိတ်ဖြာခြင်းဖြင့် သတ်မှတ်ပါက၊ 50 နှင့် 80 ကြားရှိ ကျောင်းသားများ၏ မည်သည့်ရာခိုင်နှုန်းသည် အတန်းရရှိခဲ့သနည်း။
ဤပြဿနာကိုဖြေရှင်းရန် Chebyshev ၏သီအိုရီ၏ဖော်မြူလာကိုအသုံးပြုရန်လိုအပ်သည်။ သို့သော်၊ စံနှုန်း 50 နှင့် 80 သည် ကိန်းရှင်၏ ဆိုလိုရင်းမှ မည်မျှသွေဖည်မည်ကို ကျွန်ုပ်တို့ ဦးစွာဆုံးဖြတ်ရမည်ဖြစ်ပြီး ၎င်းကိုပြုလုပ်ရန်အတွက် အောက်ပါတွက်ချက်မှုကို ရိုးရိုးရှင်းရှင်းပြုလုပ်ရန် လိုအပ်ပါသည်။
![]()
![]()
![]()
ထို့ကြောင့်၊ တန်ဘိုး 50 နှင့် 80 သည် အောက်နှင့် အထက်ဆိုလိုးမှ 1.5 စံနှုန်းများနှင့် သက်ဆိုင်ပါသည်။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် Chebysheva ၏ သီအိုရီ၏ ဖော်မြူလာကို k=1.5 ဖြင့် အသုံးပြုပါသည်။
![]()
![]()
![]()
ထို့ကြောင့် အနည်းဆုံး ကျောင်းသား 55.56% သည် 50 နှင့် 80 ကြားတွင် အတန်းတစ်ခု ရရှိခဲ့သည်။
Chebyshev ၏သီအိုရီဂဏန်းတွက်စက်
မေးခွန်းရှိတန်ဖိုးများနှင့် ပျမ်းမျှ (k) အကြား စံသွေဖည်မှုအရေအတွက်ကို ထည့်ပါ၊ ထို့နောက် “တွက်ချက်ရန်” ကိုနှိပ်ပါ။ ထို့နောက် ဂဏန်းပေါင်းစက်သည် ယုံကြည်မှုကြားကာလ၏ အနည်းဆုံးဖြစ်နိုင်ခြေကို ပြန်ပေးလိမ့်မည်။
ဒဿမ ခြားနားချက်အဖြစ် အစက်ကို အသုံးပြု၍ စံသွေဖည်မှု အရေအတွက်ကို ထည့်သွင်းရပါမည်။
Chebyshev ၏ သီအိုရီနှင့် လက်မနည်းဥပဒေ
ကိန်းဂဏန်းများဆိုင်ရာ အနီးကပ်ဆက်စပ်နေသော အယူအဆနှစ်ခုမှာ Chebyshev ၏ သီအိုရီနှင့် empirical rule ဖြစ်သောကြောင့် နှစ်ခုစလုံးသည် ယုံကြည်မှုကြားကာလများ၏ ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် အသုံးပြုသောကြောင့် ဖြစ်သည်။
Chebyshev ၏သီအိုရီနှင့် empirical rule အကြားခြားနားချက် မှာ Chebyshev ၏သီအိုရီကို မည်သည့်ဖြန့်ဖြူးမှုအမျိုးအစားတွင်မဆို အသုံးပြုနိုင်ပြီး empirical rule သည် ပုံမှန်ဖြန့်ဖြူးမှုအတွက်သာ အကျုံးဝင်သည်။
Chebyshev ၏သီအိုရီကိုအသုံးပြုခြင်းသည် ပိုမိုကျယ်ပြန့်သော်လည်း လက်တွေ့ကျသောစည်းမျဉ်းသည် ပုံမှန်ဖြန့်ဝေမှုအတွက် ပိုမိုတိကျသောရလဒ်များကိုပေးသည်။
လက်မ၏စည်းမျဉ်းကိုအတိအကျကြည့်ရန် ဤနေရာကိုနှိပ်ပါ-