Cochran's q test ဆိုတာဘာလဲ။ (အဓိပ္ပါယ် & #038; ဥပမာ)

Cochran’s Q test သည် အုပ်စုတစ်ခုစီတွင် တူညီသောပုဂ္ဂိုလ်များပေါ်လာသည့် အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသော အုပ်စုများတွင် “ အောင်မြင်မှုများ” အချိုးညီမျှခြင်းရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းစမ်းသပ်မှုတစ်ခုဖြစ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် မတူညီသောလေ့လာမှုနည်းပညာသုံးမျိုးကို အသုံးပြုသောအခါ စာမေးပွဲအောင်မြင်သော ကျောင်းသားအချိုးအစား ညီမျှခြင်းရှိမရှိ ဆုံးဖြတ်ရန် Cochran’s Q test ကို အသုံးပြုနိုင်ပါသည်။

Cochran’s Q Test လုပ်ဆောင်ရန် အဆင့်များ

Cochran’s Q test သည် အောက်ပါ null နှင့် အခြား hypotheses ကို အသုံးပြုသည် ။

Null hypothesis (H ₀ ) : “ အောင်မြင်မှုများ” ၏အချိုးအစားသည် အုပ်စုအားလုံးတွင် တူညီပါသည်။

Alternative hypothesis ( _HA ) : “ အောင်မြင်မှုများ” ၏အချိုးအစားသည် အနည်းဆုံးအုပ်စုများထဲမှ တစ်ခုတွင် မတူညီပါ။

စာမေးပွဲစာရင်းကို အောက်ပါအတိုင်း တွက်ချက်သည်။

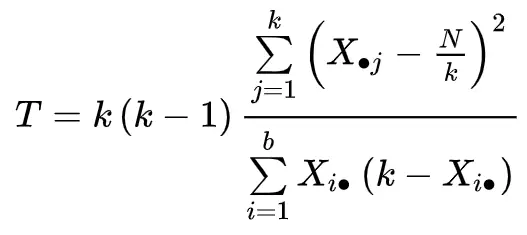
ရွှေ-

• k- ကုသမှုအရေအတွက် (သို့မဟုတ် “ အုပ်စုများ” )
• Xj- ^jth ကုသမှုအတွက် ကော်လံစုစုပေါင်း
• b: လုပ်ကွက်အရေအတွက်
• ရှီ။ : ^ith block အတွက် လိုင်းစုစုပေါင်း
• N : စုစုပေါင်း ကြီးကြီးမားမား

T စမ်းသပ်မှုကိန်းဂဏန်းသည် လွတ်လပ်မှု k-1 ဒီဂရီဖြင့် Chi-square ဖြန့်ဖြူးမှုကို လိုက်နာသည်။

စစ်ဆေးမှုစာရင်းအင်းနှင့်ဆက်စပ်သော p-တန်ဖိုးသည် အချို့သောအရေးပါမှုအဆင့် (ဥပမာ α = 0.05) အောက်တွင်ရှိနေပါက၊ ကျွန်ုပ်တို့သည် null hypothesis ကိုငြင်းပယ်နိုင်ပြီး “ အောင်မြင်မှု” အချိုးအစားသည် ကွဲပြားသည်ဟုဆိုရန် လုံလောက်သောအထောက်အထားရှိသည် ဟုကျွန်ုပ်တို့ကောက်ချက်ချနိုင်ပါသည်။ အနည်းဆုံးအုပ်စုတစ်ခု။

ဥပမာ- Cochran ၏ Q စမ်းသပ်မှု

မတူညီသော လေ့လာမှုနည်းပညာသုံးမျိုးသည် ကျောင်းသားများကြားတွင် အောင်မြင်မှုနှုန်း အချိုးအစား မတူညီနိုင်သည်ကို သုတေသီတစ်ဦးမှ သိချင်သည်ဆိုပါစို့။

၎င်းကို စမ်းသပ်ရန်၊ မတူညီသော လေ့လာမှုနည်းစနစ်သုံးမျိုးဖြင့် စာမေးပွဲတစ်ခုစီတွင် တူညီသောအခက်အခဲရှိသော ကျောင်းသား အယောက် ၂၀ ကို ခေါ်ယူခဲ့သည်။ ရလဒ်များကို အောက်တွင် ပြထားသည်။

Cochran ၏ Q စမ်းသပ်မှုကို လုပ်ဆောင်ရန်၊ ၎င်းသည် ကိုယ်တိုင်လုပ်ဆောင်ရန် ပျင်းစရာကောင်းသောကြောင့် ကျွန်ုပ်တို့သည် စာရင်းအင်းဆော့ဖ်ဝဲကို အသုံးပြုနိုင်ပါသည်။

ဤဒေတာအတွဲကို ဖန်တီးပြီး R statistical programming language ဖြင့် Cochran ၏ Q စမ်းသပ်မှုကို လုပ်ဆောင်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် ကုဒ်ဖြစ်သည်-

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

စမ်းသပ်မှုရလဒ်မှ ကျွန်ုပ်တို့သည် အောက်ပါတို့ကို ကြည့်ရှုနိုင်သည်။

• စမ်းသပ်မှုစာရင်းအင်းသည် 0.333 ဖြစ်သည်။
• သက်ဆိုင်ရာ p-value သည် 0.8465 ဖြစ်သည်။

ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။

ဆိုလိုသည်မှာ ကျောင်းသားများ အသုံးပြုသော လေ့လာမှုနည်းပညာသည် အောင်မြင်မှုနှုန်း အချိုးအစားအမျိုးမျိုးကို ဦးတည်စေသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိဟု ဆိုလိုပါသည်။