Excel တွင် cohen's d တွက်ချက်နည်း
စာရင်းဇယားများတွင်၊ အုပ်စုနှစ်ခုကြားတွင် သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်လိုပါက p-value ကို ရလဒ်ထွက်ပေါ်စေသည့် hypothesis test တစ်ခုကို ပြုလုပ်လေ့ရှိပါသည်။
အကယ်၍ ဤ p-တန်ဖိုးသည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် (အများအားဖြင့် ရွေးချယ်မှုများသည် 0.10၊ 0.05 နှင့် 0.01) သည် အုပ်စုနှစ်ခုကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိနေသည်ဟု ကျွန်ုပ်တို့ ကောက်ချက်ချပါသည်။
သို့သော်လည်း၊ အုပ်စုနှစ်ခုကြားတွင် ကိန်းဂဏန်းအချက်အလတ် သိသိသာသာကွာခြားမှု ရှိ/မရှိကို p-value က ကျွန်ုပ်တို့ကို ပြောပြနိုင်သော်လည်း အကျိုးသက်ရောက်မှုအရွယ်အစားက ထိုကွာခြားချက်မှာ အမှန်တကယ် မည်မျှကြီးမားသည်ကို ပြောပြနိုင်ပါသည်။
အကျိုးသက်ရောက်မှုအရွယ်အစား၏ အသုံးအများဆုံးတိုင်းတာမှုတစ်ခုမှာ Cohen’s d ဖြစ်ပြီး၊ အောက်ပါအတိုင်းတွက်ချက်သည်။
Cohen’s d = ( x 1 – x 2 ) / Pooled SD
ရွှေ-
- x 1 = အုပ်စု 1 ၏ ပျမ်းမျှ
- x 2 = အုပ်စု 2 ၏ ပျမ်းမျှ
- စုဖွဲ့ထားသော SD = √ (s 1 2 + s 2 2 ) / 2
ဤသင်ခန်းစာသည် Excel တွင် Cohen’s d တွက်ချက်နည်းကို ရှင်းပြထားသည်။
ဥပမာ- Excel တွင် Cohen’s d
Excel တွင် Cohen’s d ကိုတွက်ချက်ရန် အောက်ပါအဆင့်များကို ပြီးအောင်လုပ်ပါ။
အဆင့် 1: ဒေတာကိုထည့်ပါ။
ပထမ၊ အုပ်စုနှစ်စုအတွက် ပျမ်းမျှ၊ စံသွေဖည်မှုနှင့် နမူနာအရွယ်အစား (n) တို့၏ တန်ဖိုးများကို ထည့်သွင်းပါမည်။
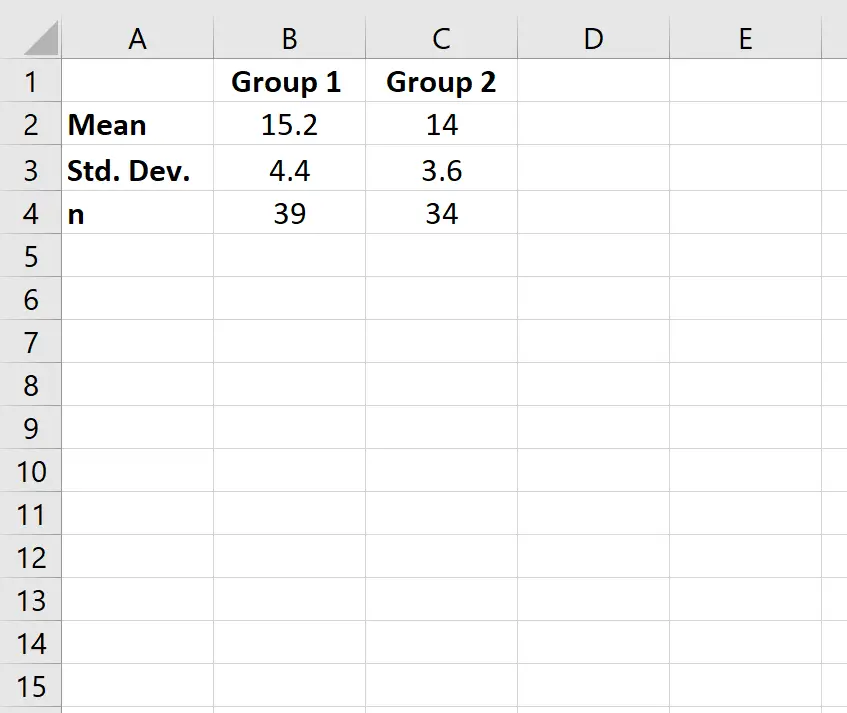
အဆင့် 2: ဆိုလိုသည်မှာ ခြားနားချက်ကို တွက်ချက်ပါ။
ထို့နောက် ကျွန်ုပ်တို့သည် အုပ်စု၏ ခြားနားချက်ကို တွက်ချက်မည်ကို ဆိုလိုသည်။
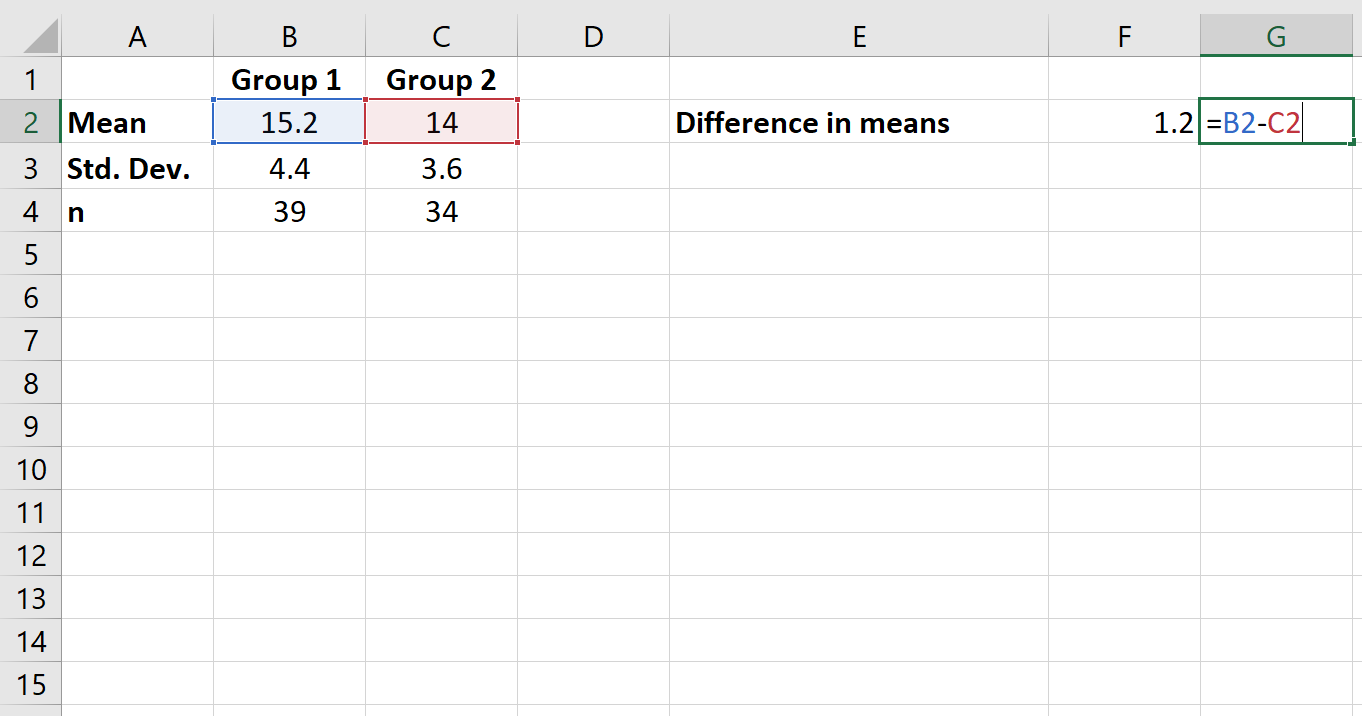
အဆင့် 3- စုပေါင်းစံနှုန်းသွေဖည်မှုကို တွက်ချက်ပါ။
ထို့နောက်၊ စုပေါင်းစံသွေဖည်မှုကို တွက်ချက်ပါမည်။
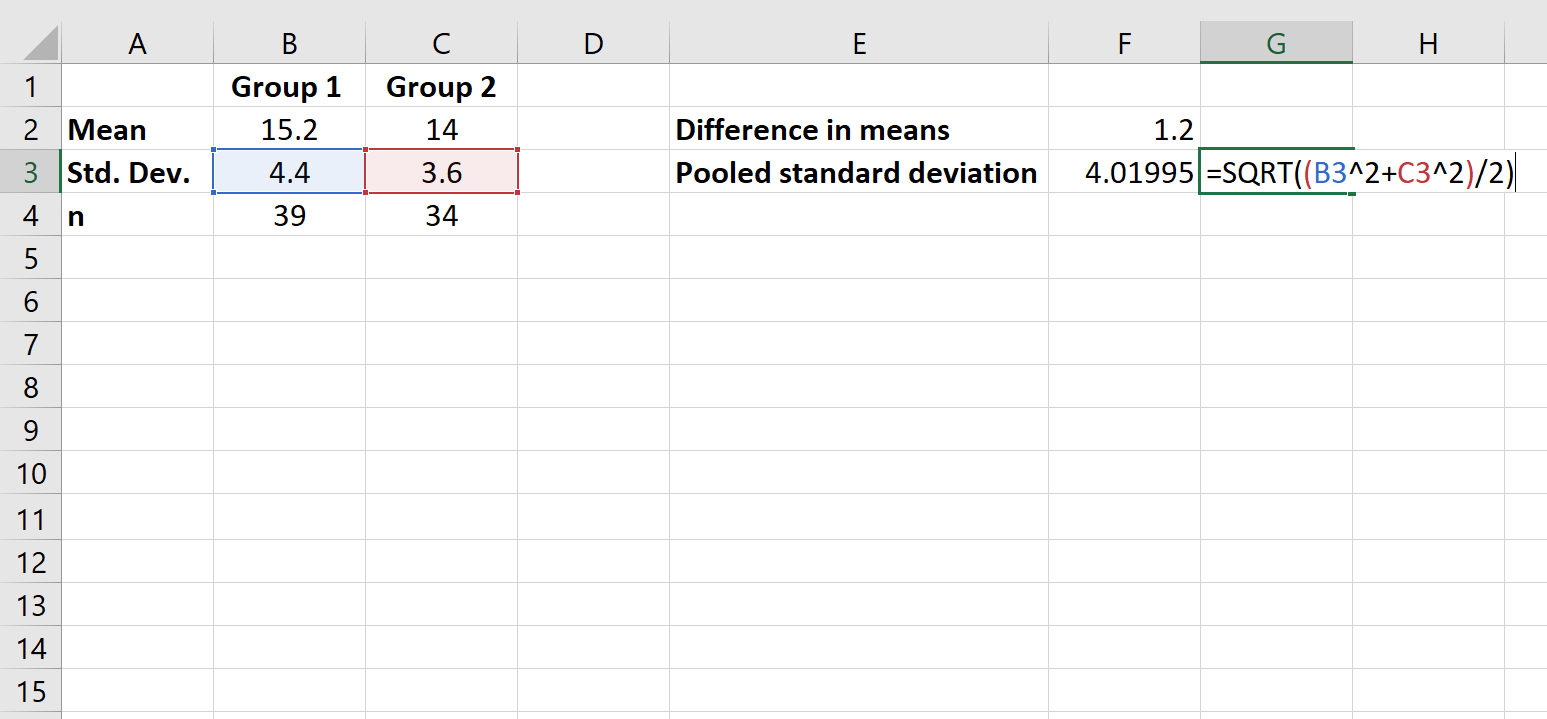
အဆင့် 4- Cohen’s d ကို တွက်ချက်ပါ။
နောက်ဆုံးတွင် Cohen’s d ကို တွက်ချက်ပါမည်။
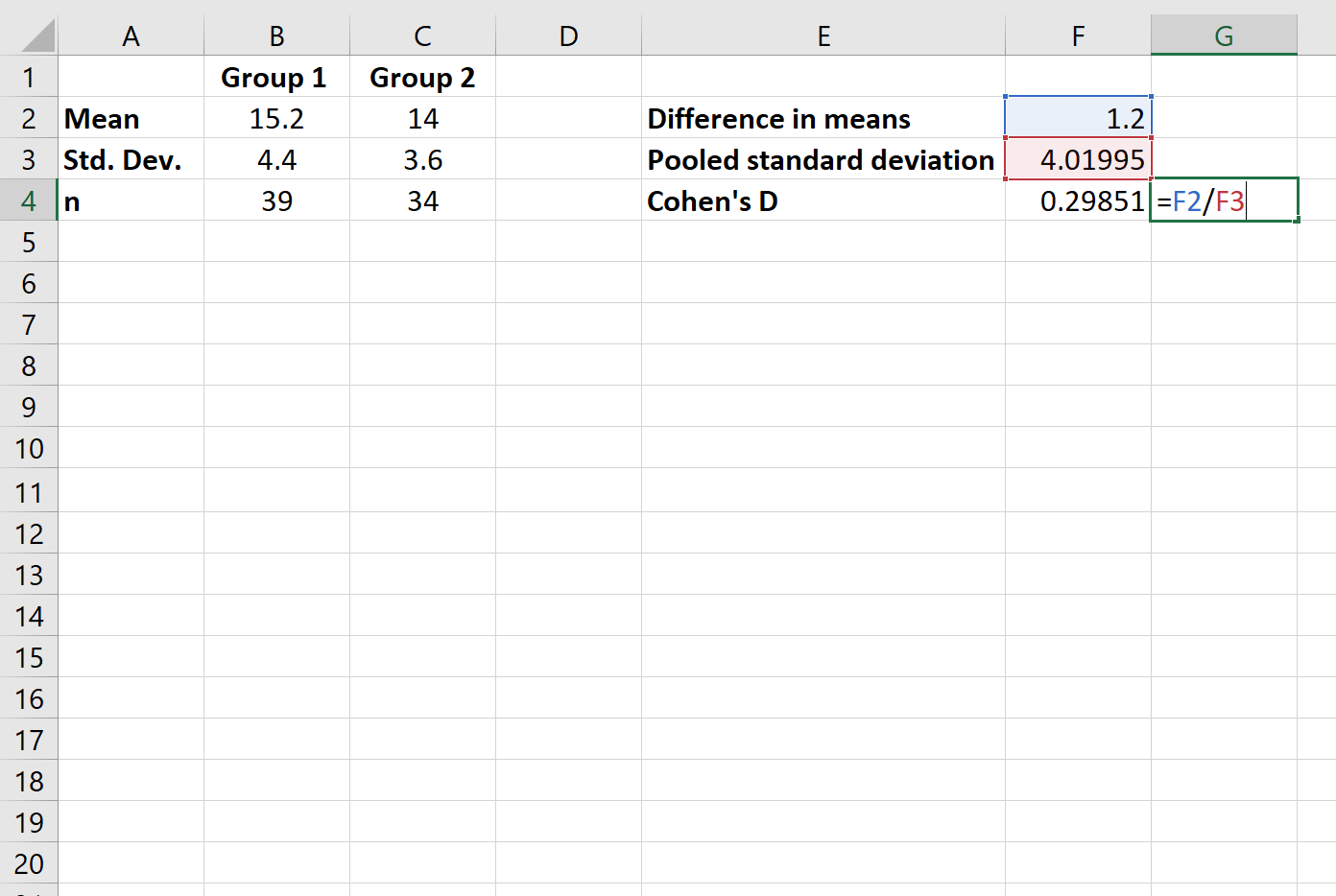
ဤဥပမာအတွက် Cohen’s d သည် 0.29851 ဖြစ်သွားသည်။
Cohen’s d ၏အဓိပ္ပာယ်ဖွင့်ဆိုပုံ
ယေဘူယျအားဖြင့် Cohen’s d ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်။
- 0.2 = သေးငယ်သောအကျိုးသက်ရောက်မှုအရွယ်အစား
- 0.5 = အလယ်အလတ်အကျိုးသက်ရောက်မှုအရွယ်အစား
- 0.8 = ကြီးမားသောအကျိုးသက်ရောက်မှုအရွယ်အစား
ကျွန်ုပ်တို့၏ဥပမာတွင်၊ အကျိုးသက်ရောက်မှုအရွယ်အစား 0.29851 သည် သေးငယ်သောအကျိုးသက်ရောက်မှုအရွယ်အစားဟု ယူဆနိုင်ဖွယ်ရှိသည်။
ဆိုလိုသည်မှာ အုပ်စုနှစ်ခု၏ နည်းလမ်းများအကြား ခြားနားချက်မှာ ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာ ကွဲပြားသော်လည်း အုပ်စုများ၏ အဓိပ္ပါယ်မှာ အမှန်တကယ် ကွာခြားချက်မှာ အရေးမပါပေ။
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။