Google sheets တွင် covariance matrix ဖန်တီးနည်း

Covariance သည် ကိန်းရှင်တစ်ခုရှိ ပြောင်းလဲမှုများနှင့် ဒုတိယကိန်းရှင်တစ်ခုရှိ အပြောင်းအလဲများနှင့် ဆက်စပ်နေပုံကို တိုင်းတာခြင်းဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ ၎င်းသည် ကိန်းရှင်နှစ်ခုအား မျဉ်းသားဆက်စပ်နေသည့်အတိုင်းအတာကို တိုင်းတာခြင်းဖြစ်သည်။

ကိန်းရှင်နှစ်ခုကြားရှိ ကွဲလွဲမှုကို တွက်ချက်ရန် ဖော်မြူလာမှာ X နှင့် Y ဖြစ်သည်-

COV( X , Y ) = Σ(x- x )(y- y ) / n

covariance matrix သည် မတူညီသော variable များစွာကြားတွင် ကွဲလွဲမှုကိုပြသသော စတုရန်း matrix တစ်ခုဖြစ်သည်။ ၎င်းသည် ဒေတာအတွဲတစ်ခုတွင် မတူညီသော variable များ မည်သို့ဆက်စပ်ကြောင်း နားလည်ရန် အသုံးဝင်သောနည်းလမ်းတစ်ခုဖြစ်သည်။

အောက်ပါ ဥပမာသည် ပေးထားသော ဒေတာအစုံအတွက် Google Sheets တွင် တူညီသော မက်ထရစ်ကို ဖန်တီးနည်းကို ပြသထားသည်။

Google Sheets တွင် Covariance Matrix ဖန်တီးနည်း

သင်္ချာ၊ သိပ္ပံနှင့် သမိုင်းဘာသာရပ်သုံးခုတွင် မတူညီသော ကျောင်းသား ၁၀ ဦး၏ စာမေးပွဲရမှတ်များကို ပြသသည့် အောက်ပါဒေတာအတွဲတစ်ခုရှိသည် ဆိုကြပါစို့။

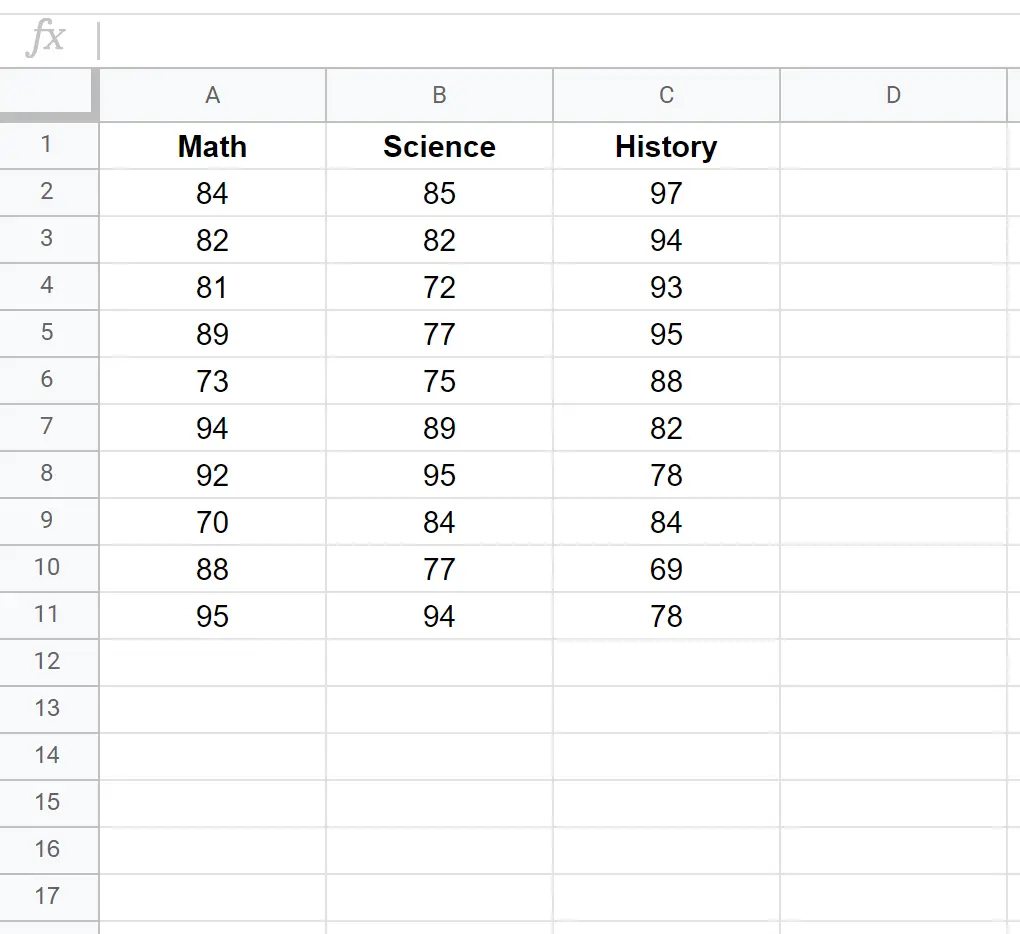
ဤဒေတာအတွဲအတွက် မတူကွဲပြားသည့်မက်ထရစ်ကို ဖန်တီးရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါအထားအသိုဖြင့် COVAR() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။

COVAR(data_y၊ data_x)

ဤဒေတာအတွဲအတွက် covariance matrix ကို ဆဲလ် B15:D17 တွင်ပြသထားသော်လည်း covariance matrix ကိုဖန်တီးရာတွင်အသုံးပြုသည့်ဖော်မြူလာများကိုအောက်ပါဆဲလ် B21:D23 တွင်ပြသထားသည်-

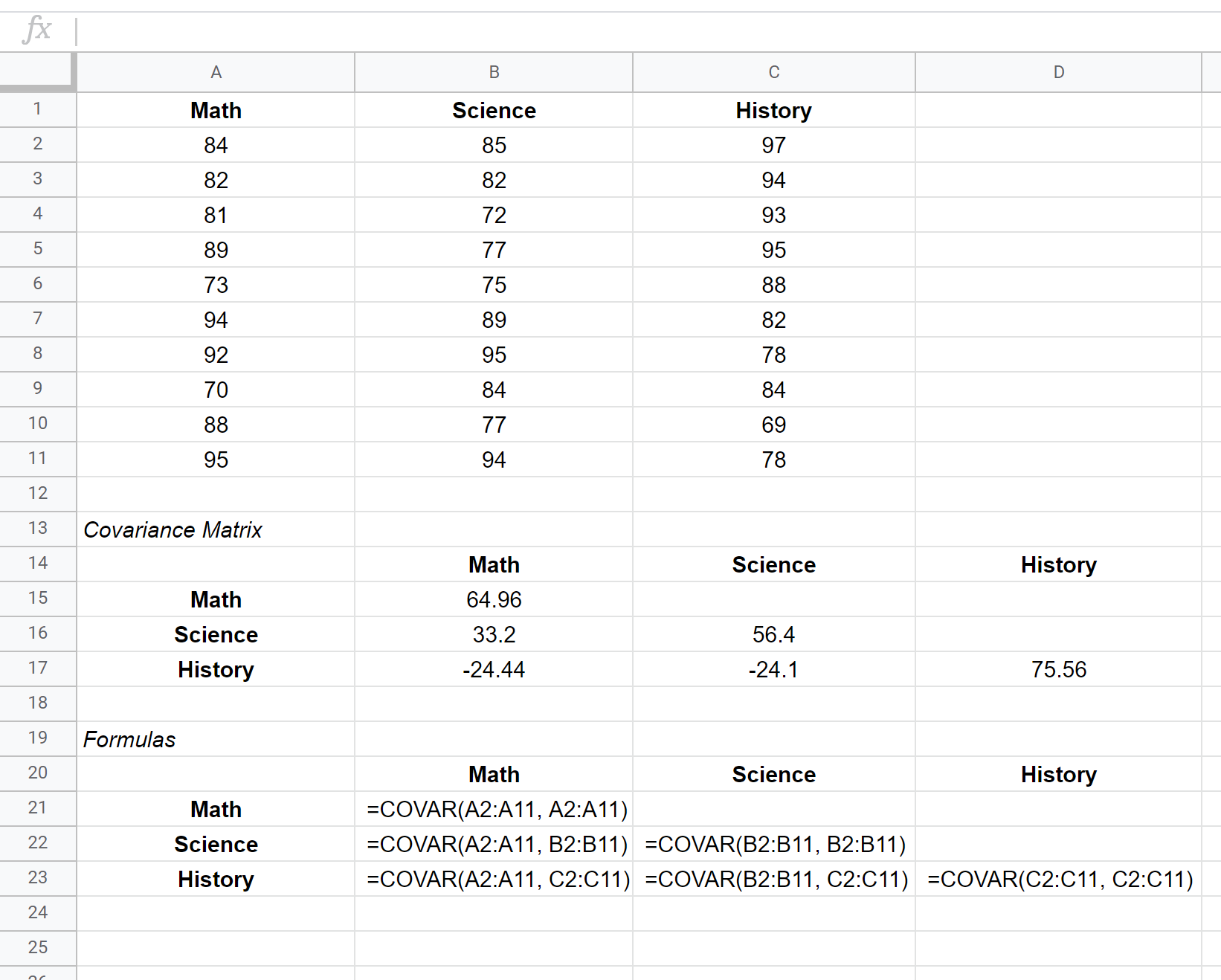
ကွဲလွဲမှုမက်ထရစ်ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။

ကျွန်ုပ်တို့တွင် ကွဲပြားသော matrix တစ်ခုရှိသည်နှင့်၊ ၎င်းသည် matrix တန်ဖိုးများကို အနက်ဖွင့်ရန် ရိုးရှင်းပါသည်။

matrix ၏ထောင့်ဖြတ်များတစ်လျှောက်ရှိတန်ဖိုးများသည် ဘာသာရပ်တစ်ခုစီ၏ကွဲလွဲမှုများဖြစ်သည်။ ဥပမာအားဖြင့်:

• သင်္ချာရမှတ်များ၏ ကွဲလွဲမှုသည် 64.96 ဖြစ်သည်။
• သိပ္ပံရမှတ်များ၏ ကွဲလွဲမှုသည် 56.4 ဖြစ်သည်။
• သမိုင်းဝင်ရမှတ်ကွဲလွဲမှုသည် 75.56 ဖြစ်သည်။

matrix ၏အခြားတန်ဖိုးများသည် မတူညီသောဘာသာရပ်များအကြား ကွဲလွဲမှုများကို ကိုယ်စားပြုသည်။ ဥပမာအားဖြင့်:

• သင်္ချာနှင့် သိပ္ပံရမှတ်များအကြား ကွာခြားချက်မှာ ၃၃.၂ ဖြစ်သည်။
• သင်္ချာနှင့် သမိုင်းရမှတ်များကြား ကွဲလွဲမှုမှာ -24.44 ဖြစ်သည်။
• သိပ္ပံနှင့် သမိုင်းရမှတ်များအကြား ကွဲလွဲမှုမှာ -24.1 ဖြစ်သည်။

ကွဲလွဲမှုများအတွက် အပြုသဘောဆောင်သော ကိန်းဂဏန်း တစ်ခုသည် ကိန်းရှင်နှစ်ခုသည် တပြိုင်နက်တွင် အတိုး သို့မဟုတ် လျော့တတ်သည်ကို ညွှန်ပြသည်။ ဥပမာအားဖြင့်၊ သင်္ချာနှင့် သိပ္ပံတွင် အပြုသဘောဆောင်သော ကွဲလွဲမှု (33.2) ရှိသည်၊ သင်္ချာတွင် အမှတ်များသော ကျောင်းသားများသည်လည်း သိပ္ပံတွင် ရမှတ်များတတ်ကြောင်း ညွှန်ပြသည်။ အလားတူပင် သင်္ချာဘာသာရပ်တွင် ညံ့ဖျင်းသော ကျောင်းသားများသည် သိပ္ပံတွင် ညံ့ဖျင်းစွာ ဖြေဆိုလေ့ရှိကြသည်။

ကွဲလွဲမှုတစ်ခုအတွက် အနုတ်ကိန်းဂဏန်း တစ်ခုသည် ကိန်းရှင်တစ်ခုတိုးလာသည်နှင့်အမျှ၊ ဒုတိယကိန်းရှင်သည် လျော့နည်းသွားကြောင်း ဖော်ပြသည်။ ဥပမာအားဖြင့်၊ သင်္ချာနှင့် သမိုင်းတွင် အနုတ်လက္ခဏာ ကွာဟချက် (-24.44) ရှိသည်၊ သင်္ချာတွင် အမှတ်များသော ကျောင်းသားများသည် သမိုင်းတွင် အမှတ်နိမ့်တတ်ကြောင်း ညွှန်ပြသည်။ အလားတူပင် သင်္ချာဘာသာရပ်တွင် အမှတ်နိမ့်သော ကျောင်းသားများသည် သမိုင်းတွင် ရမှတ်များ မြင့်မားတတ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

Excel တွင် Covariance Matrix ဖန်တီးနည်း
R တွင် ကွဲပြားသော မက်ထရစ်ကို ဖန်တီးနည်း
Python တွင် Covariance Matrix ဖန်တီးနည်း
SPSS တွင် Covariance Matrix ဖန်တီးနည်း