ကွဲလွဲမှု မက်ထရစ်ကို ဘယ်လိုဖတ်မလဲ။

Covariance သည် ကိန်းရှင်တစ်ခုရှိ ပြောင်းလဲမှုများနှင့် ဒုတိယကိန်းရှင်တစ်ခုရှိ အပြောင်းအလဲများနှင့် ဆက်စပ်နေပုံကို တိုင်းတာခြင်းဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ ၎င်းသည် ကိန်းရှင်နှစ်ခုအား မျဉ်းသားဆက်စပ်နေသည့်အတိုင်းအတာကို တိုင်းတာခြင်းဖြစ်သည်။

covariance matrix သည် မတူညီသော variable များစွာကြားတွင် ကွဲလွဲမှုကိုပြသသော စတုရန်း matrix တစ်ခုဖြစ်သည်။ ၎င်းသည် ဒေတာအတွဲတစ်ခုတွင် မတူညီသော variable များ မည်သို့ဆက်စပ်ကြောင်း နားလည်ရန် အသုံးဝင်သောနည်းလမ်းတစ်ခုဖြစ်သည်။

အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့တွင် ကွဲပြားမှုမက်ထရစ်ကို မည်သို့ဖတ်ရမည်ကို ပြသထားသည်။

ကွဲလွဲမှု မက်ထရစ်ကို ဘယ်လိုဖတ်မလဲ။

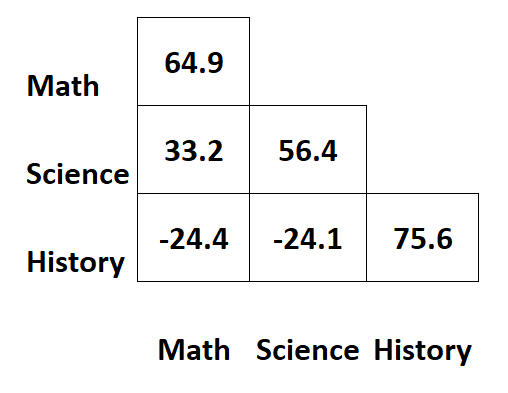
ကျောင်းသားများအတွက် မတူညီသောဘာသာရပ်သုံးမျိုးအတွက် စာမေးပွဲရမှတ်များအကြောင်း အချက်အလက်ပါရှိသော ကျွန်ုပ်တို့တွင် အောက်ဖော်ပြပါ ကွဲပြားသည့် matrix ရှိသည်ဆိုပါစို့။

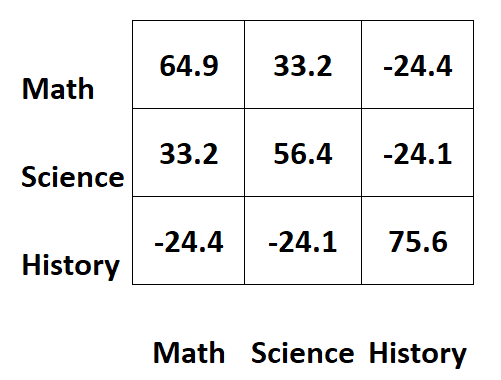
matrix ၏ ထောင့်ဖြတ်များတစ်လျှောက် တန်ဖိုးများသည် ဘာသာရပ်တစ်ခုစီ၏ ကွဲပြားမှုများကို ကိုယ်စားပြုသည်။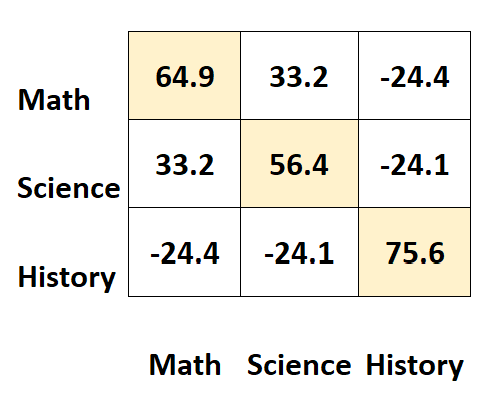

ဥပမာအားဖြင့်:

• သင်္ချာရလဒ်များ၏ကွဲလွဲမှုသည် 64.9 ဖြစ်သည်။
• သိပ္ပံရမှတ်များ၏ ကွဲလွဲမှုသည် 56.4 ဖြစ်သည်။
• သမိုင်းဝင်ရမှတ်များ၏ကွဲလွဲမှုသည် 75.6 ဖြစ်သည်။

matrix ၏အခြားတန်ဖိုးများသည် မတူညီသောဘာသာရပ်များအကြား ကွဲလွဲမှုများကို ကိုယ်စားပြုသည်။

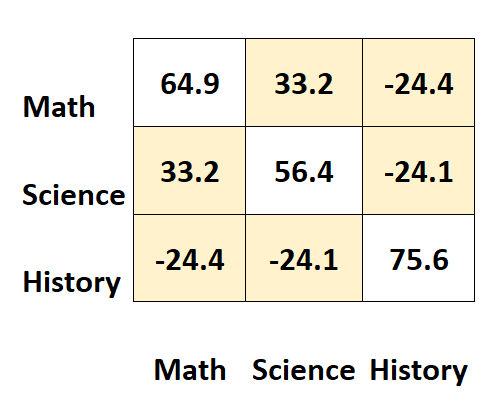
ဥပမာအားဖြင့်:

• သင်္ချာနှင့် သိပ္ပံရမှတ်များကြား ကွာခြားချက်မှာ ၃၃.၂ ဖြစ်သည်။
• သင်္ချာနှင့် သမိုင်းရမှတ်များကြား ကွဲလွဲမှုမှာ -24.4 ဖြစ်သည်။
• သိပ္ပံနှင့် သမိုင်းရမှတ်များအကြား ကွဲလွဲမှုမှာ -24.1 ဖြစ်သည်။

ကွဲလွဲမှုများအတွက် အပြုသဘောဆောင်သော ကိန်းဂဏန်း တစ်ခုသည် ကိန်းရှင်နှစ်ခုသည် တပြိုင်နက်တွင် အတိုး သို့မဟုတ် လျော့တတ်သည်ကို ညွှန်ပြသည်။

ဥပမာအားဖြင့်၊ သင်္ချာနှင့် သိပ္ပံတွင် အပြုသဘောဆောင်သော ကွဲလွဲမှု ( 33.2 ) တွင် သင်္ချာရမှတ်များ မြင့်မားသော ကျောင်းသားများသည် သိပ္ပံတွင် ရမှတ်များ မြင့်မားလေ့ရှိကြောင်း ညွှန်ပြပါသည်။

အပြန်အလှန်အားဖြင့် သင်္ချာဘာသာရပ်တွင် ညံ့ဖျင်းသော ကျောင်းသားများသည် သိပ္ပံဘာသာရပ်တွင် ညံ့ဖျင်းလေ့ရှိသည်။

ကွဲလွဲမှုတစ်ခုအတွက် အနုတ်ကိန်းဂဏန်း တစ်ခုသည် ကိန်းရှင်တစ်ခုတိုးလာသည်နှင့်အမျှ၊ ဒုတိယကိန်းရှင်သည် လျော့နည်းသွားကြောင်း ဖော်ပြသည်။

ဥပမာအားဖြင့်၊ သင်္ချာနှင့် သမိုင်းသည် အနုတ်လက္ခဏာ ( -24.44 ) တွင် သင်္ချာဘာသာရပ်တွင် မြင့်မားသော ကျောင်းသားများသည် သမိုင်းတွင် နိမ့်ကျတတ်ကြောင်း ညွှန်ပြသည်။

ဆန့်ကျင်ဘက်အားဖြင့် သင်္ချာဘာသာရပ်တွင် အမှတ်နိမ့်သော ကျောင်းသားများသည် သမိုင်းတွင် ရမှတ်မြင့်မားလေ့ရှိသည်။

covariance matrix ၏ symmetry ဆိုင်ရာ မှတ်စု

ကွဲပြားမှု matrix သည် ပြီးပြည့်စုံစွာ အချိုးကျကြောင်း သတိပြုသင့်သည်။

ဥပမာ၊ ညာဘက်အပေါ်ဆုံးဆဲလ်က ဘယ်ဘက်အောက်ခြေဆဲလ်နဲ့ အတိအကျတူညီတဲ့တန်ဖိုးကို ပြပါတယ်-

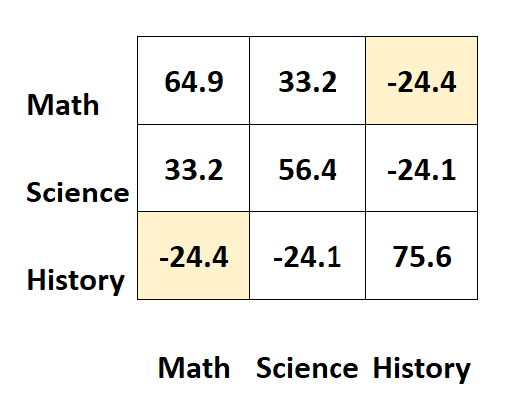
အမှန်မှာ၊ ဆဲလ်နှစ်ခုသည် သမိုင်းနှင့် သင်္ချာအကြား ကွဲလွဲမှုကို တိုင်းတာသည်။

covariance matrix သည် symmetric ဖြစ်သောကြောင့် matrix တွင်ပြသထားသော coariance value တစ်ဝက်သည် မလိုအပ်တော့၍ မလိုအပ်ပါ။

ထို့ကြောင့်၊ တစ်ခါတစ်ရံတွင် ကွဲလွဲမှု matrix ၏ ထက်ဝက်ကိုသာ ပြသလိမ့်မည်-

ကွဲပြားသော matrix ကို မည်သည့်အချိန်တွင် အသုံးပြုရမည်နည်း။

လက်တွေ့တွင်၊ သင်သည် coariance matrix ထက် ဆက်စပ်မက်ထရစ်ကို မကြာခဏဖန်တီးပြီး အဓိပ္ပါယ်ပြန်ဆိုရန် လိုအပ်ပါသည်။

သို့ရာတွင်၊ ကွဲပြားသော စက်သင်ယူမှုဆိုင်ရာ အယ်လဂိုရီသမ်များနှင့် မော်ဒယ်များအတွက် တူညီသောမက်ထရစ်များကို “ အဖုံးအောက်” တွင် သုံးလေ့ရှိသည်။

ဥပမာအားဖြင့်၊ ကိန်းရှင်အမြောက်အများပါဝင်သော ဒေတာအတွဲတစ်ခု၏ အရင်းခံပုံစံများကို နားလည်ရန် ကူညီပေးသည့် အဓိကအစိတ်အပိုင်းများကို ခွဲခြမ်းစိတ်ဖြာမှုတွင် ၊ covariance matrix ကို အသုံးပြုသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် မတူညီသော ကိန်းဂဏန်းဆိုင်ရာဆော့ဖ်ဝဲကို အသုံးပြု၍ covariance matrix ကိုဖန်တီးနည်းကို ရှင်းပြသည်-

R တွင် ကွဲပြားသော မက်ထရစ်ကို ဖန်တီးနည်း
Python တွင် Covariance Matrix ဖန်တီးနည်း
SPSS တွင် Covariance Matrix ဖန်တီးနည်း
Excel တွင် Covariance Matrix ဖန်တီးနည်း