Python တွင်ကုဗလဆုတ်ယုတ်မှုလုပ်ဆောင်နည်း

Cubic regression သည် ကိန်းရှင်များကြား ဆက်နွှယ်မှုမဟုတ်သောအခါတွင် ကြိုတင်တွက်ဆထားသောကိန်းရှင်နှင့် တုံ့ပြန်ကိန်းရှင်ကြားရှိ ဆက်နွယ်မှုကို တွက်ချက်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သော ဆုတ်ယုတ်မှုအမျိုးအစားတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာတွင် Python တွင် ကုဗလဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- Python ရှိ ကုဗလဆုတ်ယုတ်မှု

ကျွန်ုပ်တို့တွင် variable နှစ်ခု (x နှင့် y) ပါရှိသော အောက်ပါပန်ဒါ DataFrame ရှိသည်ဆိုပါစို့။

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' x ': [6, 9, 12, 16, 22, 28, 33, 40, 47, 51, 55, 60],
                   ' y ': [14, 28, 50, 64, 67, 57, 55, 57, 68, 74, 88, 110]})

#view DataFrame
print (df)

     xy
0 6 14
1 9 28
2 12 50
3 16 64
4 22 67
5 28 57
6 33 55
7 40 57
8 47 68
9 51 74
10 55 88
11 60 110

ဤဒေတာ၏ ရိုးရှင်းသော ခွဲခြမ်းစိပ်ဖြာမှုတစ်ခုကို ပြုလုပ်ပါက၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွှယ်မှုသည် မျဉ်းမညီကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

 import matplotlib. pyplot as plt

#create scatterplot
plt. scatter (df. x , df. y ) 

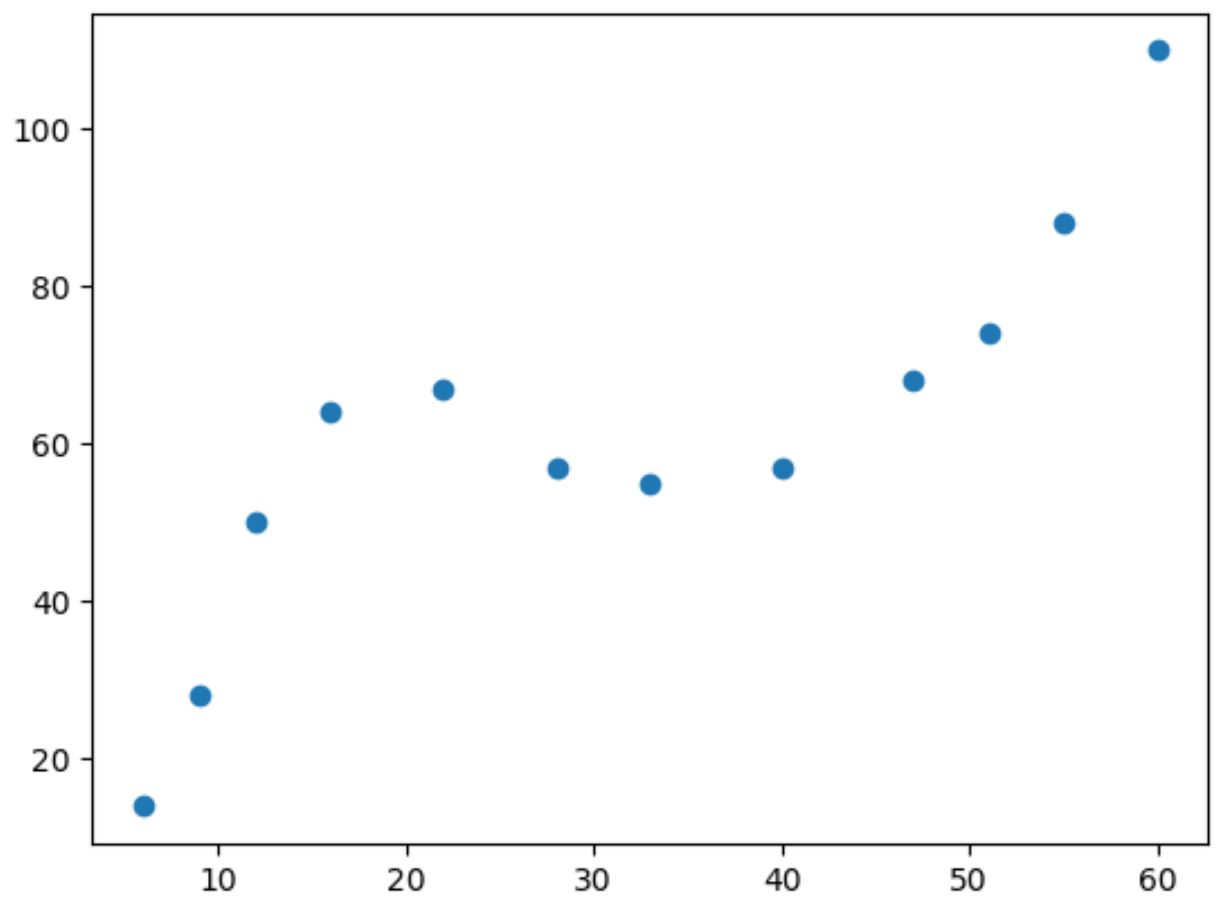
x ၏တန်ဖိုးတိုးလာသည်နှင့်အမျှ y သည် သတ်မှတ်ထားသောအမှတ်သို့တိုးလာပြီး လျော့နည်းသွားသည်၊ ထို့နောက် ထပ်တိုးလာသည်။

ကွက်ကွက်ရှိ “ မျဉ်းကွေး” နှစ်ခုပါသော ဤပုံစံသည် ကိန်းရှင်နှစ်ခုကြားရှိ ကုဗိပ်ဆက်နွယ်မှုကို ညွှန်ပြနေသည်။

ဆိုလိုသည်မှာ cubic regression model သည် variable နှစ်ခုကြားရှိ ဆက်နွယ်မှုကို quantify လုပ်ရန်အတွက် ကောင်းမွန်သော ကိုယ်စားလှယ်လောင်းဖြစ်သည်။

ကုဗလဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန်၊ numpy.polyfit() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဒီဂရီ 3 ပါသော ကိန်းဂဏန်းပမာဏ ဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့ ဖြည့်သွင်းနိုင်သည်-

 import numpy as np

#fit cubic regression model
model = np. poly1d (np. polyfit (df. x , df. y , 3))

#add fitted cubic regression line to scatterplot
polyline = np. linspace (1, 60, 50)
plt. scatter (df. x , df. y )
plt. plot (polyline, model(polyline))

#add axis labels
plt. xlabel (' x ')
plt. ylabel (' y ')

#displayplot
plt. show () 

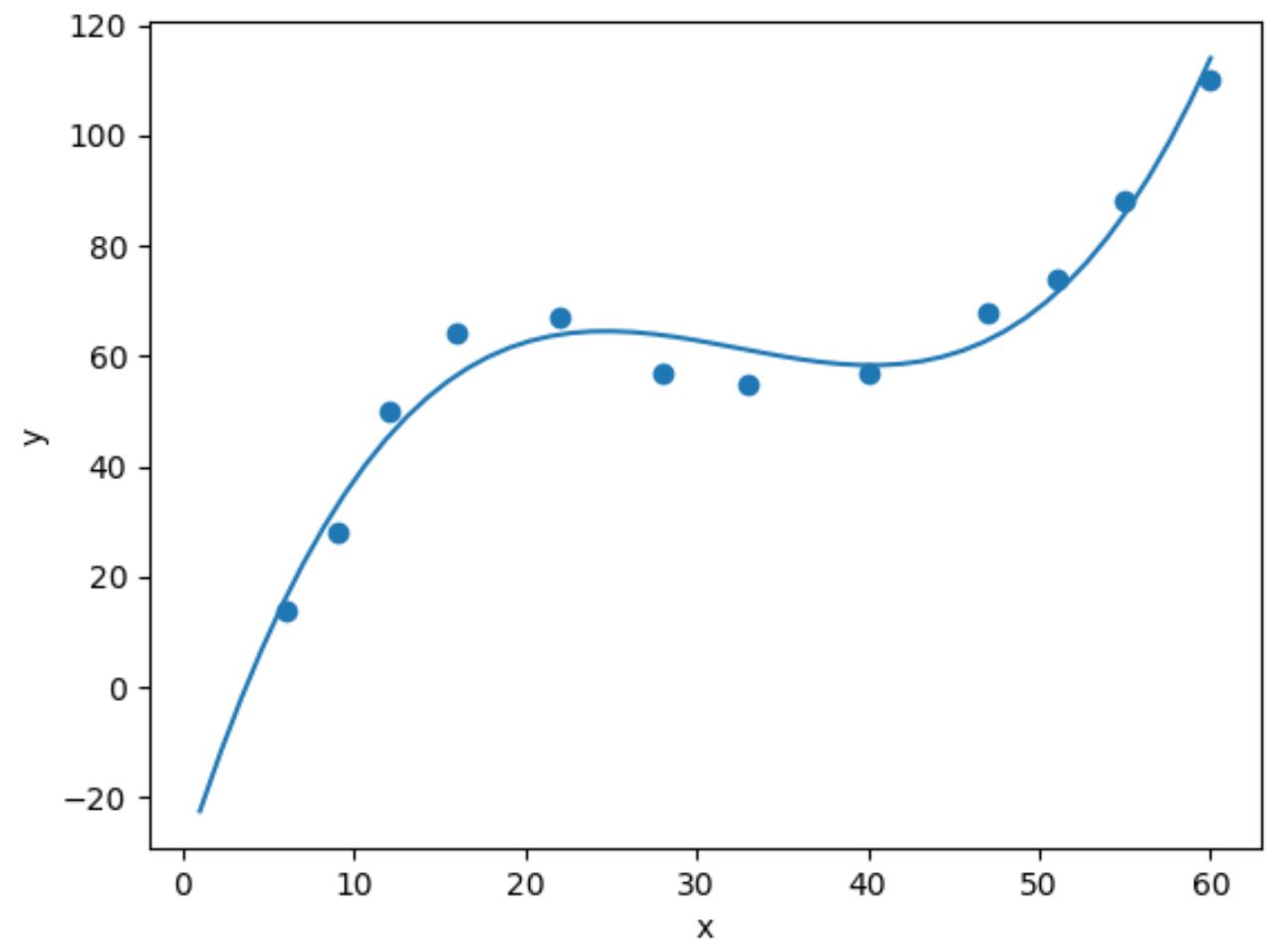
မော်ဒယ် coefficients များကို ရိုက်နှိပ်ခြင်းဖြင့် တပ်ဆင်ထားသော ကုဗဆုတ်ဆုတ်ညီမျှခြင်းကို ကျွန်ုပ်တို့ ရယူနိုင်ပါသည်။

 print (model)

          3 2
0.003302x - 0.3214x + 9.832x - 32.01

တပ်ဆင်ထားသော ကုဗဆုတ်ဆုတ်ညီမျှခြင်းမှာ-

y = 0.003302(x) ³ – 0.3214(x) ² + 9.832x – 30.01

x ၏တန်ဖိုးအပေါ်အခြေခံ၍ y ၏မျှော်မှန်းတန်ဖိုးကိုတွက်ချက်ရန် ဤညီမျှခြင်းကိုအသုံးပြုနိုင်သည်။

ဥပမာ၊ x သည် 30 ဖြစ်ပါက၊ y အတွက် မျှော်မှန်းတန်ဖိုးမှာ 64.844 ဖြစ်သည် ။

y = 0.003302(30) ³ – 0.3214(30) ² + 9.832(30) – 30.01 = 64.844

မော်ဒယ်၏ R-squared ကိုရရန် အတိုချုံးရေးနိုင်သည်၊ ၎င်းသည် ခန့်မှန်းသူကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏အချိုးအစားဖြစ်သည်။

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np. polyfit (x, y, degree)
    p = np. poly1d (coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np. sum (y)/len(y)
    ssreg = np. sum ((yhat-ybar) ** 2)
    sstot = np. sum ((y - ybar) ** 2)
    results[' r_squared '] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(df. x , df. y , 3)

{'r_squared': 0.9632469890057967}

ဤဥပမာတွင်၊ မော်ဒယ်၏ R စတုရန်းသည် 0.9632 ဖြစ်သည်။

ဆိုလိုသည်မှာ တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှု 96.32% ကို ခန့်မှန်းသူကိန်းရှင်က ရှင်းပြနိုင်သည်။

ဤတန်ဖိုးသည် အလွန်မြင့်မားသောကြောင့်၊ ကုဗလဆုတ်ယုတ်မှုပုံစံသည် ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုကို ကောင်းမွန်စွာ တွက်ချက်ပေးကြောင်း ၎င်းကဆိုသည်။

ဆက်စပ်မှု- ကောင်းသော R-squared တန်ဖိုးဆိုသည်မှာ အဘယ်နည်း။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါ သင်ခန်းစာများသည် Python တွင် အခြားသော အသုံးများသော အလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Python တွင် ရိုးရှင်းသော linear regression လုပ်ဆောင်နည်း
Python တွင် quadratic regression လုပ်ဆောင်နည်း
Python တွင် polynomial regression လုပ်နည်း