Curvilinear regression ဆိုတာ ဘာလဲ။ (အဓိပ္ပါယ်နှင့် ဥပမာများ)
Curvilinear regression သည် မျဉ်းဖြောင့်မဟုတ်ပဲ မျဉ်းကွေး နှင့် အံဝင်ခွင်ကျဖြစ်အောင် ကြိုးစားသည့် မည်သည့် regression model အတွက်မဆို ပေးထားသော အမည်ဖြစ်သည်။
curvilinear regression model ၏ ယေဘူယျ ဥပမာများ ပါဝင်သည်။
Quadratic regression- ခန့်မှန်းသူကိန်းရှင်တစ်ခုနှင့် တုံ့ပြန်မှုကိန်းရှင် ကြားတွင် လေးထောင့်ပုံသဏ္ဍာန်ဆက်နွယ်မှုရှိသည့်အခါ အသုံးပြုသည်။ ဂရပ်ဖစ်ပြသောအခါ၊ ဤဆက်နွယ်မှုအမျိုးအစားသည် ကွဲလွဲမှုတစ်ခုပေါ်ရှိ “ U” သို့မဟုတ် ပြောင်းပြန် “ U” နှင့်တူသည်-
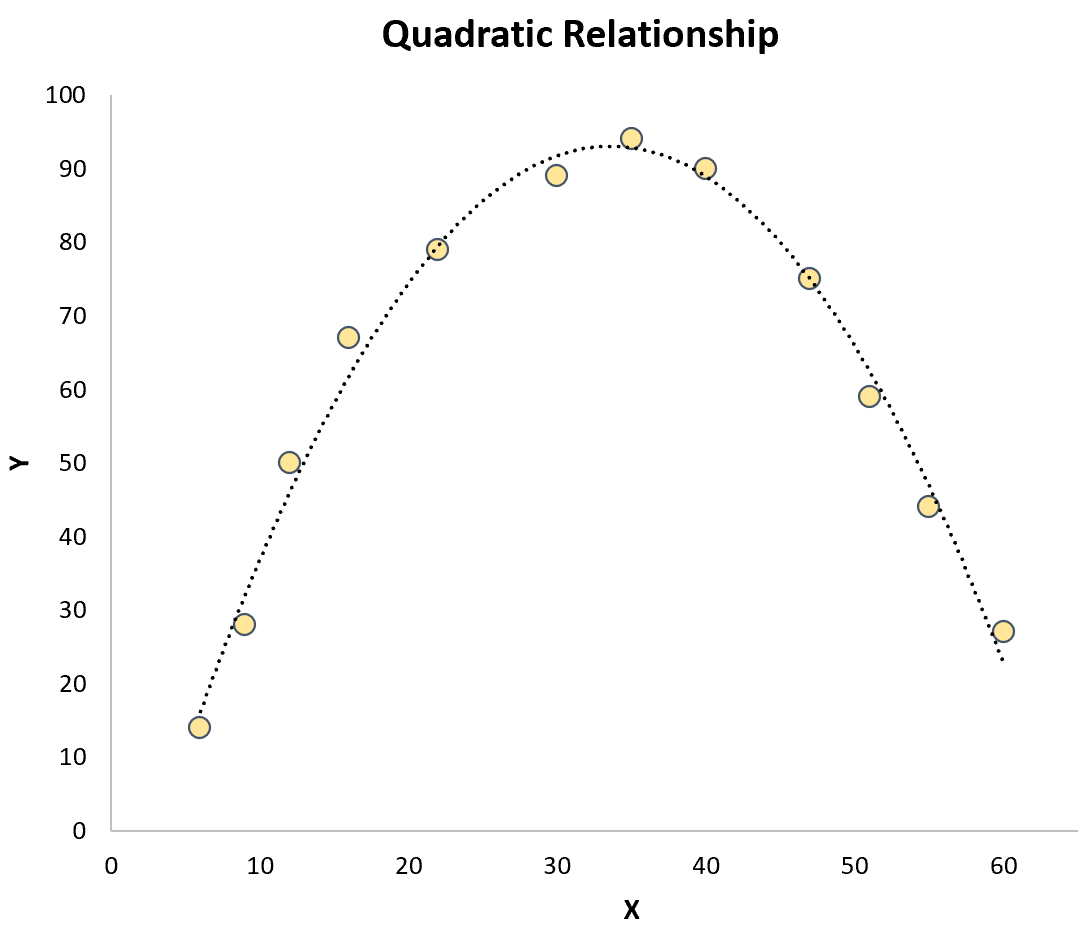
Cubic Regression- ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်တစ်ခုကြားတွင် ကုဗိပ်ဆက်နွယ်မှုရှိသည့်အခါ အသုံးပြုသည်။ ဂရပ်ဖစ်ပြသောအခါ၊ ဤဆက်နွယ်မှုအမျိုးအစားသည် ကွဲအက်မှုတစ်ခုပေါ်တွင် ကွဲပြားသောမျဉ်းကွေးနှစ်ခုကို ပြသသည်-
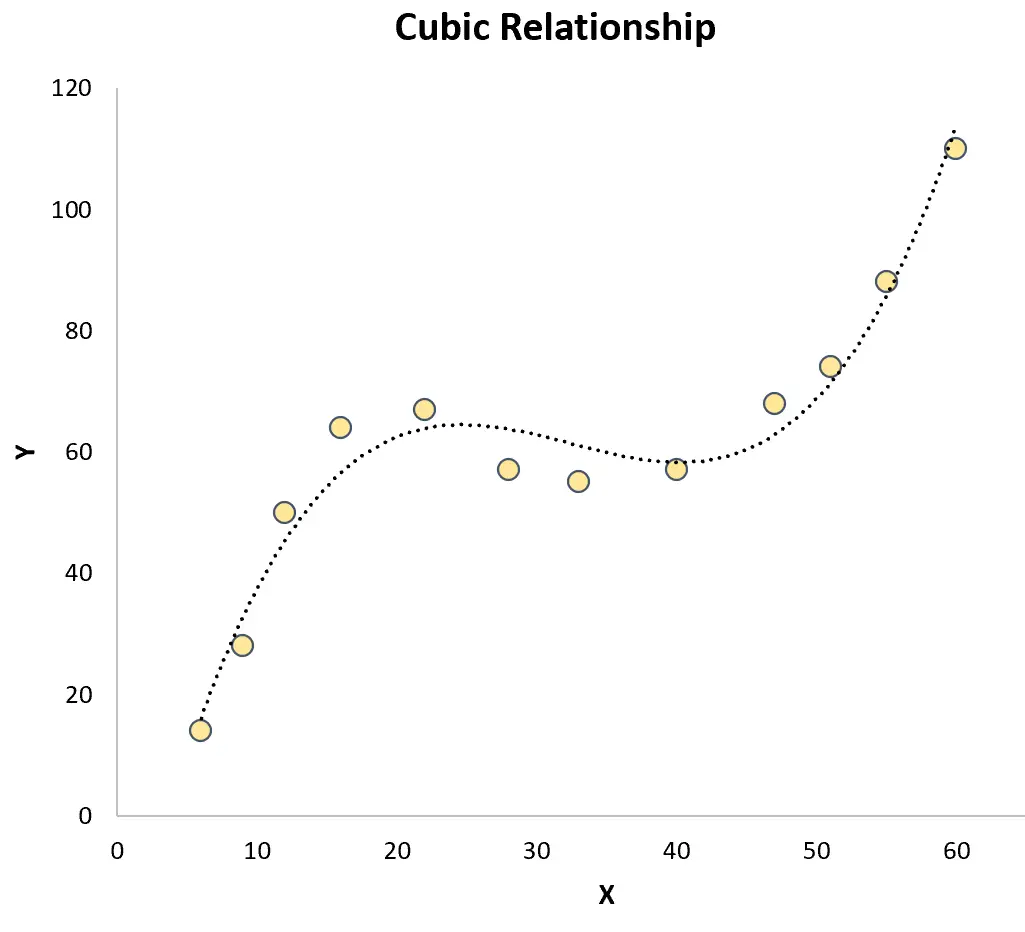
ဤနှစ်ခုစလုံးသည် ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်သည် တစ်ပြေးညီဖြစ်နေသော ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု နှင့် ဆန့်ကျင်ဘက်ဖြစ်သည်။
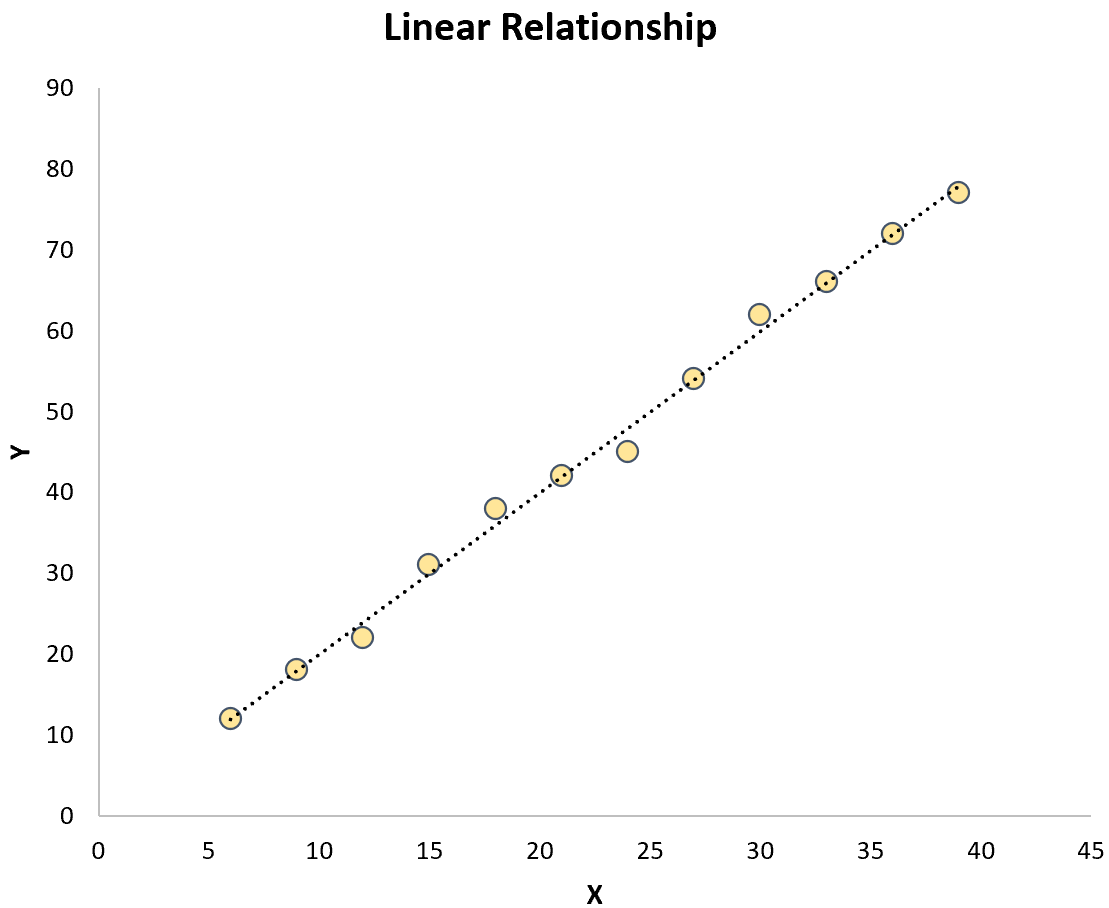
curvilinear regression မော်ဒယ်များအတွက် ဖော်မြူလာ
ရိုးရှင်းသော linear regression model သည် အောက်ပါဖော်မြူလာကို အသုံးပြု၍ ဒေတာအစုတစ်ခုအား အံဝင်ခွင်ကျဖြစ်အောင် ကြိုးပမ်းသည်-
ŷ = β 0 + β 1 x
ရွှေ-
- ŷ- တုံ့ပြန်မှု ကိန်းရှင်
- β 0 , β 1 – ဆုတ်ယုတ်မှုကိန်းဂဏန်းများ
- x- ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်
ဆန့်ကျင်ဘက်အားဖြင့်၊ လေးပုံတစ်ပုံ ဆုတ်ယုတ်မှုပုံစံသည် အောက်ပါဖော်မြူလာကို အသုံးပြုသည်-
ŷ = β 0 + β 1 x + β 2 x 2
ထို့အပြင် ကုဗလဆုတ်ယုတ်မှုပုံစံသည် အောက်ပါဖော်မြူလာကို အသုံးပြုသည်-
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
ထပ်ကိန်းများပါ၀င်သော ဆုတ်ယုတ်မှုပုံစံများအတွက် ပေးထားသော နောက်ထပ်ယေဘုယျအမည်မှာ အောက်ဖော်ပြပါဖော်မြူလာကို ယူဆောင်သည့် ပေါလီအမည်ဆုတ်ယုတ်မှု ဖြစ်သည်။
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
k ၏တန်ဖိုးသည် polynomial ၏ ဒီဂရီကို ဖော်ပြသည်။ ဒီဂရီသည် မည်သည့်ကိန်းဂဏန်းမဆို အပြုသဘောဆောင်နိုင်သော်လည်း လက်တွေ့တွင် ကျွန်ုပ်တို့သည် 3 သို့မဟုတ် 4 ထက်ကြီးသောဒီဂရီဖြင့် polynomial regression မော်ဒယ်များနှင့် ကိုက်ညီခဲပါသည်။
ဆုတ်ယုတ်မှုပုံစံဖော်မြူလာတွင် ထပ်ကိန်းများကိုအသုံးပြုခြင်းဖြင့်၊ မျဉ်းဖြောင့်များအစား မျဉ်းကြောင်းများ အစား မျဉ်းကြောင်းများဆိုင်ရာ နှိုင်းယှဥ်မှုပုံစံများသည် ဒေတာအတွဲများနှင့် ကိုက်ညီနိုင်မည်ဖြစ်သည်။
curvilinear regression ကို ဘယ်အချိန်မှာ သုံးရမလဲ
curvilinear regression ကို အသုံးပြုသင့်သည် ၊ မသင့်ကို သိရန် အလွယ်ဆုံးနည်းလမ်းမှာ ခန့်မှန်းသူ variable နှင့် တုံ့ပြန်မှု variable ၏ အပိုင်းခွဲတစ်ခုကို ဖန်တီးရန်ဖြစ်သည်။
scatterplot သည် variable နှစ်ခုကြားရှိ linear ဆက်နွယ်မှုကို ပြသပါက၊ ရိုးရိုး linear regression သည် သင့်လျော်ပါသည်။
သို့ရာတွင်၊ ခွဲခြမ်းစိတ်ဖြာချက်သည် ခန့်မှန်းသူနှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား လေးထောင့်ပုံ၊ ကုဗ သို့မဟုတ် အခြား curvilinear ပုံစံကို ပြသပါက၊ curvilinear regression ကို အသုံးပြုရန် ပိုသင့်လျော်ပါသည်။
ရိုးရှင်းသော linear regression model နှင့် curvilinear regression model တို့ကိုလည်း ဖြည့်စွက်နိုင်ပြီး data နှင့် အသင့်တော်ဆုံး မော်ဒယ်တစ်ခုစီ၏ တပ်ဆင်ထားသော R-squared တန်ဖိုးများကို နှိုင်းယှဉ်ဆုံးဖြတ်နိုင်သည်။
ချိန်ညှိထားသော R-squared သည် တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှုမည်မျှရှိသည်ကို ပြောပြနိုင်သောကြောင့် မော်ဒယ်ရှိ ခန့်မှန်းသူကိန်းရှင်အရေအတွက်အတွက် ချိန်ညှိထားသော ခန့်မှန်းကိန်းရှင်ကိန်းရှင်(များ) က ရှင်းပြနိုင်သောကြောင့် အသုံးဝင်သည်။
ယေဘူယျအားဖြင့်၊ အမြင့်ဆုံးချိန်ညှိထားသော R-squared တန်ဖိုးရှိသော မော်ဒယ်သည် ဒေတာအစုံနှင့် ပိုမိုကိုက်ညီမှုရှိသည်။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ကွဲပြားသော စာရင်းအင်းဆော့ဖ်ဝဲလ်တွင် ကိန်းဂဏန်းများ ကိန်းဂဏန်းများ ဆုတ်ယုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-
Polynomial Regression နိဒါန်း
Excel တွင် Polynomial Regression ကို မည်သို့လုပ်ဆောင်မည်နည်း။
Python တွင် polynomial regression လုပ်နည်း
R တွင် polynomial regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။