Anova ယူဆချက်များကို စစ်ဆေးနည်း

တစ်လမ်းသွား ANOVA သည် သုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော သီးခြားအုပ်စုများ၏ နည်းလမ်းများကြားတွင် သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည့် ကိန်းဂဏန်းစမ်းသပ်မှုတစ်ခုဖြစ်သည်။

ဤသည်မှာ တစ်လမ်းမောင်း ANOVA ကို အသုံးပြုသည့်အခါ ဥပမာတစ်ခုဖြစ်သည်။

ကျောင်းသား 90 မှ 30 ယောက်ကို အုပ်စုသုံးစုခွဲပြီး အတန်းတစ်တန်းကို ကျပန်းခွဲပေးပါသည်။ အဖွဲ့တစ်ခုစီသည် စာမေးပွဲအတွက် ပြင်ဆင်ရန် တစ်လအတွက် မတူညီသော လေ့လာမှုနည်းစနစ်ကို အသုံးပြုပါသည်။ လကုန်တွင် ကျောင်းသားအားလုံး စာမေးပွဲကို အတူတူဖြေဆိုကြသည်။

သင်ကြားမှုနည်းပညာသည် စာမေးပွဲရမှတ်များအပေါ် သက်ရောက်မှုရှိမရှိ သိလိုပါသည်။ ထို့ကြောင့် သင်သည် အုပ်စုသုံးစု၏ ပျမ်းမျှရမှတ်များကြားတွင် ကိန်းဂဏန်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် တစ်လမ်းမောင်း ANOVA ကို သင်လုပ်ဆောင်သည်။

တစ်လမ်းမောင်း ANOVA ကို မလုပ်ဆောင်မီ၊ ယူဆချက် သုံးခုနှင့် ကိုက်ညီကြောင်း ဦးစွာ စစ်ဆေးရပါမည်။

1. Normality – နမူနာတစ်ခုစီကို ပုံမှန်ဖြန့်ဝေထားသော လူဦးရေမှ ထုတ်ယူထားပါသည်။

2. သာတူညီမျှကွဲလွဲမှုများ – နမူနာများထုတ်ယူသည့် လူဦးရေ၏ကွဲလွဲမှုများသည် တူညီသည်။

3. လွတ်လပ်ရေး – အဖွဲ့တစ်ခုစီအတွင်းရှိ လေ့လာတွေ့ရှိချက်များသည် တစ်ခုနှင့်တစ်ခု အမှီအခိုကင်းပြီး အဖွဲ့များအတွင်းမှ လေ့လာချက်များကို ကျပန်းနမူနာဖြင့် ရယူခဲ့ပါသည်။

ဤယူဆချက်များနှင့် မကိုက်ညီပါက၊ ကျွန်ုပ်တို့၏ တစ်လမ်းတည်းဖြစ်သော ANOVA ၏ ရလဒ်များသည် ယုံကြည်စိတ်ချနိုင်မည်မဟုတ်ပေ။

ဤယူဆချက်များအား မည်သို့စစ်ဆေးရမည်ကို ဤဆောင်းပါးတွင် ကျွန်ုပ်တို့ ရှင်းပြထားပြီး ၎င်းတို့အနက်မှ တစ်စုံတစ်ရာကို ချိုးဖောက်ပါက မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ယူဆချက် 1- ပုံမှန်အခြေအနေ

ANOVA သည် နမူနာတစ်ခုစီကို ပုံမှန်ဖြန့်ဝေနေသည့် လူဦးရေမှ ထုတ်ယူသည်ဟု ယူဆသည်။

R တွင် ဤယူဆချက်ကို မည်သို့စစ်ဆေးရမည်နည်း။

ဤယူဆချက်ကို အတည်ပြုရန်၊ ကျွန်ုပ်တို့သည် ချဉ်းကပ်မှုနှစ်ခုကို အသုံးပြုနိုင်သည်။

• Histograms သို့မဟုတ် QQ ကွက်များကို အသုံးပြု၍ အယူအဆကို အမြင်အာရုံဖြင့် စစ်ဆေးပါ။
• Shapiro-Wilk၊ Kolmogorov-Smironov၊ Jarque-Barre သို့မဟုတ် D’Agostino-Pearson ကဲ့သို့သော တရားဝင်စာရင်းအင်းစစ်ဆေးမှုများကို အသုံးပြု၍ အယူအဆကို အတည်ပြုပါ။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ပရိုဂရမ် A၊ ပရိုဂရမ် B သို့မဟုတ် ပရိုဂရမ် C ကို တစ်လကြာ လိုက်နာရန် လူ 30 ကို ကျပန်းသတ်မှတ်ပေးသည့် ကိုယ်အလေးချိန်စမ်းသပ်မှုတွင် ပါဝင်ရန် လူ 90 ကို ခေါ်ယူသည်ဆိုပါစို့။ ပရိုဂရမ်သည် ကိုယ်အလေးချိန်ကျခြင်းအပေါ် သက်ရောက်မှုရှိမရှိ သိရန်၊ တစ်လမ်းမောင်း ANOVA ကို လုပ်ဆောင်လိုပါသည်။ အောက်ပါကုဒ်သည် histograms၊ QQ plots နှင့် Shapiro-Wilk စမ်းသပ်မှုတို့ကို အသုံးပြု၍ ပုံမှန်အဖြစ်ယူဆချက်ကို မည်သို့စစ်ဆေးရမည်ကို သရုပ်ပြသည်။

1. ANOVA မော်ဒယ်ကို အံကိုက်ပါ။

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. တုံ့ပြန်မှုတန်ဖိုးများ၏ ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးပါ။

 #create histogram
hist(data$weight_loss)

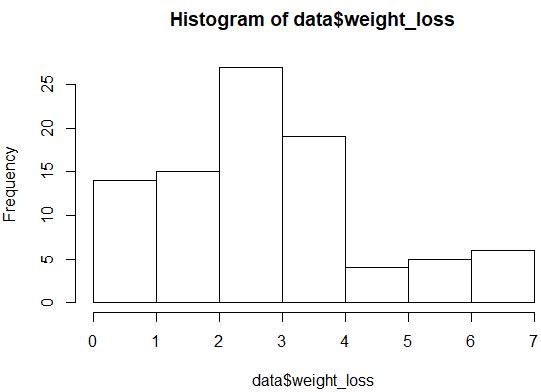
ဖြန့်ဖြူးမှုသည် သာမန်အားဖြင့် ဖြန့်ဝေပုံမပေါ်ပါ (ဥပမာ၊ ၎င်းသည် “ ခေါင်းလောင်း” ပုံသဏ္ဍာန်မဟုတ်ပါ)၊ သို့သော် ဖြန့်ဖြူးမှုကို နောက်ထပ်ကြည့်ရှုရန် QQ ကွက်ကွက်တစ်ခုကိုလည်း ဖန်တီးနိုင်သည်။

3. ကျန်ရှိသော QQ ကွက်တစ်ခုကို ဖန်တီးပါ။

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

ယေဘုယျအားဖြင့်၊ ဒေတာအမှတ်များသည် QQ ကွက်ကွက်တစ်ခုရှိ ဖြောင့်ထောင့်ဖြတ်မျဉ်းတစ်လျှောက်တွင် ရှိနေပါက၊ ဒေတာအစုံသည် ပုံမှန်ဖြန့်ဖြူးမှုနောက်ဆက်တွဲဖြစ်နိုင်သည်။ ဤကိစ္စတွင်၊ အဆုံးများတစ်လျှောက် မျဉ်းကြောင်းမှ သိသာထင်ရှားစွာ သွေဖည်သွားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်၊ ၎င်းသည် ဒေတာကို ပုံမှန်ဖြန့်ဝေခြင်းမရှိကြောင်း ညွှန်ပြနိုင်သည်။

4. ပုံမှန်အခြေအနေအတွက် Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်ပါ။

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

Shapiro-Wilk စမ်းသပ်မှုတွင် နမူနာများသည် ပုံမှန်ဖြန့်ဝေမှုမှမဟုတ်သည့် အခြားယူဆချက်များနှင့် ဆန့်ကျင်ဘက်ဖြစ်သော ပုံမှန်ဖြန့်ဝေမှုမှ ဆင်းသက်လာသည်ဟူသော အချည်းနှီးသောယူဆချက်ကို စမ်းသပ်သည်။ ဤကိစ္စတွင်၊ စမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.005999 ဖြစ်ပြီး၊ ၎င်းသည် 0.05 ၏ အယ်လ်ဖာအဆင့်ထက် နိမ့်သည်။ ၎င်းသည် နမူနာများသည် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုအား မလိုက်နာကြောင်း အကြံပြုသည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်ရမလဲ။

ယေဘူယျအားဖြင့်၊ နမူနာအရွယ်အစားများ လုံလောက်စွာကြီးနေသရွေ့ ပုံမှန်ဖြစ်ရိုးဖြစ်စဉ်ယူဆချက်အား ချိုးဖောက်မှုများအတွက် တစ်လမ်းသွား ANOVA သည် အတော်လေး ကြံ့ခိုင်သည်ဟု ယူဆပါသည်။

ထို့အပြင်၊ သင့်တွင် အလွန်ကြီးမားသောနမူနာများရှိပါက Shapiro-Wilk စမ်းသပ်မှုကဲ့သို့သော ကိန်းဂဏန်းစမ်းသပ်မှုများသည် သင့်ဒေတာသည် ပုံမှန်မဟုတ်ကြောင်း အမြဲလိုလိုပြောပြလိမ့်မည်။ ထို့ကြောင့်၊ histograms နှင့် QQ ကွက်များကဲ့သို့သော ဇယားများကို အသုံးပြု၍ သင်၏ဒေတာကို အမြင်အာရုံဖြင့် စစ်ဆေးခြင်းသည် အကောင်းဆုံးဖြစ်သည်။ ဂရပ်များကို ကြည့်ရုံဖြင့် ဒေတာများကို ပုံမှန်ဖြန့်ဝေခြင်း ရှိ၊

သာမန်ဖြစ်ရိုးဖြစ်စဉ်၏ယူဆချက်အား ပြင်းထန်စွာ ချိုးဖောက်ပါက သို့မဟုတ် သင်သည် အလွန်ရှေးရိုးဆန်သူဖြစ်လိုပါက၊ သင့်တွင် ရွေးချယ်စရာနှစ်ခုရှိသည်။

(၁) ဖြန့်ဝေမှုများကို ပုံမှန်အတိုင်း ပိုမိုဖြန့်ဝေနိုင်ရန် သင့်ဒေတာ၏ တုံ့ပြန်မှုတန်ဖိုးများကို ပြောင်းလဲပါ။

(၂) ပုံမှန်အခြေအနေဟု ယူဆရန်မလိုအပ်သော Kruskal-Wallis စမ်းသပ်မှု ကဲ့သို့သော ညီမျှသောမဟုတ်သော စမ်းသပ်စစ်ဆေးမှုကို ပြုလုပ်ပါ။

ယူဆချက် #2- တူညီသောကွဲလွဲမှု

နမူနာများကို ထုတ်ယူသည့် လူဦးရေ၏ ကွဲလွဲမှုများသည် တူညီသည်ဟု ANOVA က ယူဆသည်။

R တွင် ဤယူဆချက်ကို မည်သို့စစ်ဆေးရမည်နည်း။

ချဉ်းကပ်မှု နှစ်ခုကို အသုံးပြု၍ ဤယူဆချက်အား R ဖြင့် အတည်ပြုနိုင်သည်-

• ဘောက်စ်ကွက်များကို အသုံးပြု၍ အယူအဆကို အမြင်အာရုံဖြင့် စစ်ဆေးပါ။
• Bartlett’s test ကဲ့သို့သော တရားဝင်စာရင်းအင်းစစ်ဆေးမှုများကို အသုံးပြု၍ အယူအဆကို စမ်းသပ်ပါ။

အောက်ဖော်ပြပါကုဒ်သည် ကျွန်ုပ်တို့ယခင်ကဖန်တီးထားသည့် အလေးချိန်ဆုံးရှုံးမှုဒေတာအတွဲကို အသုံးပြု၍ ၎င်းကိုပြုလုပ်နည်းကို သရုပ်ပြသည်။

1. အကွက်ကွက်များ ဖန်တီးပါ။

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

အုပ်စုတစ်ခုစီရှိ ကိုယ်အလေးချိန်ကျခြင်း၏ ကွဲလွဲမှုကို အကွက်တစ်ခုစီ၏ အရှည်ဖြင့် စောင့်ကြည့်နိုင်သည်။ အကွက်ရှည်လေ၊ ကွဲလွဲမှု ပိုများလေဖြစ်သည်။ ဥပမာအားဖြင့်၊ Program A နှင့် Program B တို့နှင့် နှိုင်းယှဉ်ပါက ပရိုဂရမ် C တွင်ပါဝင်သူများအတွက် ကွဲလွဲမှုအနည်းငယ်ပိုများသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

2. Bartlett စမ်းသပ်မှုကို လုပ်ဆောင်ပါ။

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

Bartlett test သည် နမူနာများတွင် တူညီသောကွဲလွဲမှု မရှိသည့် အခြားယူဆချက်နှင့် တူညီသောကွဲလွဲမှုများရှိနေကြောင်း Bartlett test သည် null hypothesis ကို စမ်းသပ်သည်။ ဤကိစ္စတွင်၊ စမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.01599 ဖြစ်ပြီး၊ ၎င်းသည် 0.05 ၏ alpha အဆင့်ထက် နိမ့်သည်။ ဤသည်မှာ နမူနာများအားလုံးတွင် တူညီသောကွဲလွဲမှု မရှိသည်ကို ညွှန်ပြပါသည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်ရမလဲ။

ယေဘူယျအားဖြင့်၊ အုပ်စုတစ်ခုစီသည် နမူနာအရွယ်အစားရှိသရွေ့ တူညီသောကွဲလွဲမှုယူဆချက်အား ချိုးဖောက်မှုအတွက် တစ်လမ်းသွား ANOVA ကို မျှတစွာခိုင်ခံ့သည်ဟု ယူဆပါသည်။

သို့သော်၊ နမူနာအရွယ်အစားများ တူညီခြင်းမရှိပါက၊ ဤယူဆချက်အား ပြင်းထန်စွာချိုးဖောက်ပါက၊ Kruskal-Wallis စမ်းသပ်မှုအစား၊ သင်သည် တစ်လမ်းသွား ANOVA ၏ parametric ဗားရှင်းမဟုတ်သော Kruskal-Wallis စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်။

ယူဆချက် နံပါတ် ၃- လွတ်လပ်ရေး

ANOVA က ယူဆသည်

• အုပ်စုတစ်ခုစီ၏ လေ့လာတွေ့ရှိချက်များသည် အခြားအုပ်စုအားလုံး၏ လေ့လာတွေ့ရှိချက်များနှင့် အမှီအခိုကင်းပါသည်။
• အုပ်စုတစ်ခုစီရှိ လေ့လာတွေ့ရှိချက်များကို ကျပန်းနမူနာဖြင့် ရယူခဲ့ပါသည်။

ဤယူဆချက်ကို မည်သို့အတည်ပြုရမည်နည်း။

အုပ်စုတစ်ခုစီရှိ လေ့လာတွေ့ရှိချက်များသည် သီးခြားလွတ်လပ်ပြီး ၎င်းတို့ကို ကျပန်းနမူနာဖြင့် ရယူထားကြောင်း အတည်ပြုရန် သင်အသုံးပြုနိုင်သည့် တရားဝင်စမ်းသပ်မှု မရှိပါ။ ဤယူဆချက်ကို ကျေနပ်စေရန် တစ်ခုတည်းသောနည်းလမ်းမှာ ကျပန်းပုံစံဒီဇိုင်းကို အသုံးပြုခြင်းဖြစ်သည်။

ဒီယူဆချက်ကို မလေးစားရင် ဘာလုပ်ရမလဲ။

ကံမကောင်းစွာဖြင့်၊ ဤယူဆချက်နှင့်မကိုက်ညီပါက သင်လုပ်ဆောင်နိုင်မှုများစွာမရှိပါ။ ရိုးရှင်းစွာပြောရလျှင် အုပ်စုတစ်ခုစီရှိ လေ့လာတွေ့ရှိချက်များသည် အခြားအဖွဲ့များ၏ လေ့လာတွေ့ရှိချက်များနှင့် အမှီအခိုကင်းကင်းသော နည်းလမ်းဖြင့် ဒေတာများကို စုဆောင်းခဲ့လျှင် သို့မဟုတ် အုပ်စုတစ်ခုစီရှိ လေ့လာချက်များကို ကျပန်းစနစ်ဖြင့် မရရှိပါက၊ ANOVA ရလဒ်များသည် ယုံကြည်စိတ်ချရမည်မဟုတ်ပါ။ .

ဤယူဆချက်နှင့် မကိုက်ညီပါက၊ လုပ်ဆောင်ရမည့် အကောင်းဆုံးအရာမှာ ကျပန်းပုံစံဖြင့် စမ်းသပ်မှုကို ပြန်လည်ဖန်တီးခြင်းဖြစ်သည်။

နောက်ထပ်ဖတ်ရန်:

တစ်လမ်းမောင်း ANOVA ကို R ဖြင့် မည်သို့လုပ်ဆောင်ရမည်နည်း။
Excel တွင် One-Way ANOVA လုပ်ဆောင်နည်း