Anova မော်ဒယ်တွင် အကြွင်းအကျန်များကို ခွဲခြမ်းစိတ်ဖြာနည်း
ANOVA (“ ကွဲလွဲမှုကို ခွဲခြမ်းစိတ်ဖြာခြင်း” ) သည် သုံးမျိုး သို့မဟုတ် ထို့ထက်ပိုသော သီးခြားအုပ်စုများ၏ နည်းလမ်းများအကြား သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည့် ပုံစံတစ်မျိုးဖြစ်သည်။
ကျွန်ုပ်တို့သည် ANOVA မော်ဒယ်တစ်ခုအား ဒေတာအစုတစ်ခုသို့ တပ်ဆင်သည့်အခါတိုင်း၊ အကြွင်းအကျန်များ အမြဲရှိလိမ့်မည် – ၎င်းတို့သည် တစ်ဦးချင်းစီ၏ စူးစမ်းလေ့လာမှုနှင့် လေ့လာတွေ့ရှိမှုမှရရှိလာသော အုပ်စု၏ ဆိုလိုရင်းအကြား ကွာခြားချက်ကို ကိုယ်စားပြုသည်။
အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့တွင် ANOVA မော်ဒယ်အတွက် အကြွင်းအကျန်များကို တွက်ချက်နည်းကို ပြသထားသည်။
ဥပမာ- ANOVA တွင် အကြွင်းအကျန်များကို တွက်ချက်ခြင်း။
ကျွန်ုပ်တို့သည် ပရိုဂရမ် A၊ ပရိုဂရမ် B သို့မဟုတ် ပရိုဂရမ် C ကို တစ်လကြာ လိုက်နာရန် လူ 30 ကို ကျပန်းတာဝန်ပေးသည့် ကိုယ်အလေးချိန် လျှော့ချစမ်းသပ်မှုတွင် ပါဝင်ရန် လူ 90 ကို စုဆောင်းထားသည်ဆိုပါစို့။
ပရိုဂရမ်သုံးခုမှ ထွက်ပေါ်လာသော ကိုယ်အလေးချိန်ကျခြင်းကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်နိုင်သည်။
ပရိုဂရမ်တစ်ခုစီတွင် ပါဝင်သူတစ်ဦးချင်းစီ၏ ပျမ်းမျှကိုယ်အလေးချိန်ကို အောက်ပါအတိုင်း တွက်ချက်မည်ဆိုပါစို့။
- အစီအစဉ် A : 1.58 ပေါင်
- ပရိုဂရမ် B : 2.56 ပေါင်
- ပရိုဂရမ် C : 4.13 ပေါင်
ANOVA မော်ဒယ်မှ အကြွင်းအကျန်များသည် လူတစ်ဦးစီ၏ ကိုယ်အလေးချိန်ကျခြင်းနှင့် ၎င်းတို့၏ ပရိုဂရမ်၏ ပျမ်းမျှကိုယ်အလေးချိန်အကြား ကွာခြားချက်ဖြစ်သည်။
ဥပမာအားဖြင့်၊ အောက်ဖော်ပြပါဇယားသည် လေ့လာမှုတွင် မတူညီသော လူ ၁၀ ဦးအတွက် အကြွင်းအကျန်များကို တွက်ချက်နည်းကို ပြသသည်-
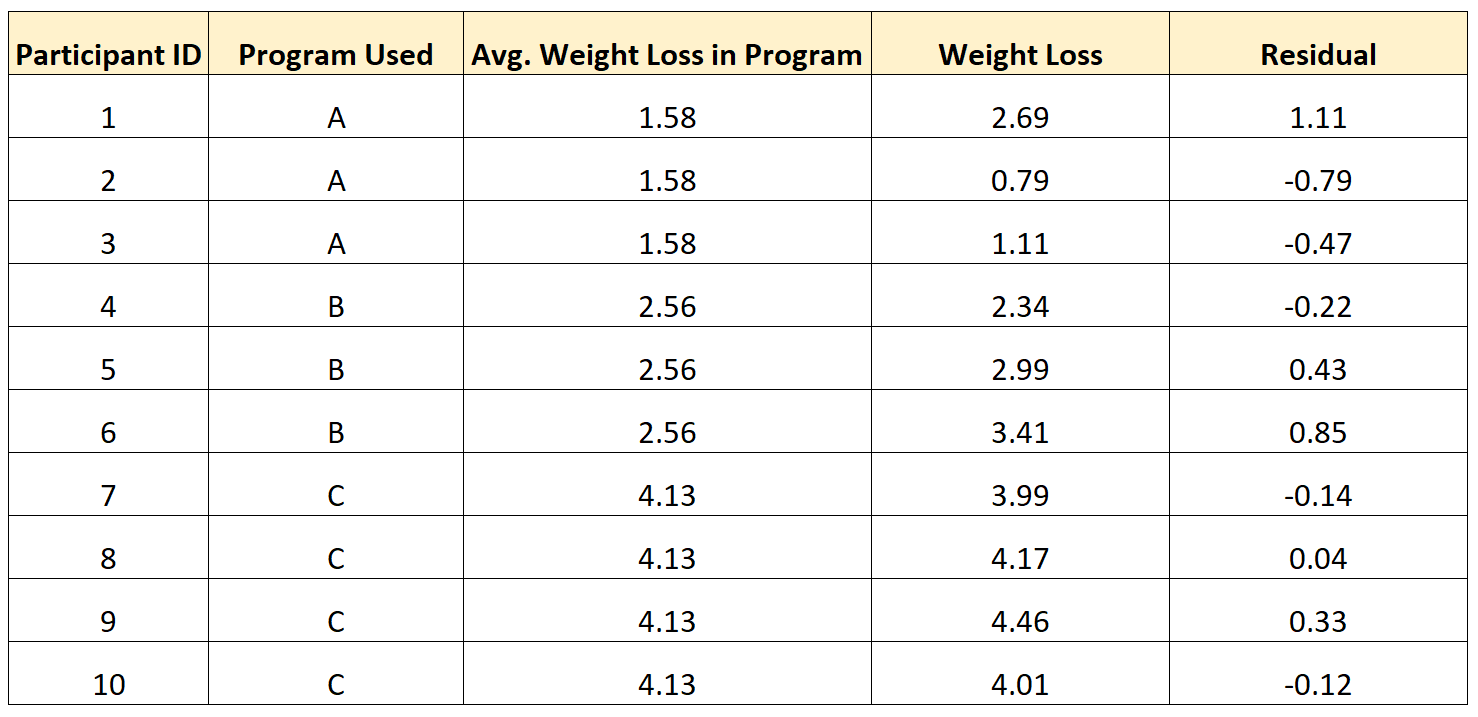
အောက်ပါပုံစံကို သတိပြုပါ။
- ၎င်းတို့၏ အုပ်စု ပျမ်းမျှထက် တန်ဖိုးရှိသော ပုဂ္ဂိုလ်များသည် အပေါင်းလက္ခဏာ ကျန်ရှိနေပါသည်။
- မိမိတို့အုပ်စုထက် နိမ့်ကျသောတန်ဖိုးရှိသူများသည် အနုတ်လက္ခဏာ ကျန်ရှိနေသည်။
လက်တွေ့တွင်၊ ကျွန်ုပ်တို့သည် လူ 90 လုံးအတွက် အကြွင်းအကျန်များကို တွက်ချက်ပါသည်။
ပုံမှန်အခြေအနေစစ်ဆေးရန် အကြွင်းအကျန်များကို အသုံးပြုနည်း
ANOVA ၏ ယူဆချက် တစ်ခုသည် ကျန်အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေခြင်းဖြစ်သည်။
ဤယူဆချက်ကို အတည်ပြုရန် အသုံးအများဆုံးနည်းလမ်းမှာ QQ ကွက်ကွက် ဖန်တီးရန်ဖြစ်သည်။
အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေပါက၊ QQ ကွက်ကွက်ရှိ အမှတ်များသည် ဖြောင့်ထောင့်ဖြတ်မျဉ်းပေါ်တွင် တည်ရှိနေမည်ဖြစ်သည်။
ဤသည်မှာ ကျွန်ုပ်တို့၏ယခင်နမူနာအတွက် QQ ဇာတ်ကွက်သည် မည်သို့မည်ပုံဖြစ်သည်-
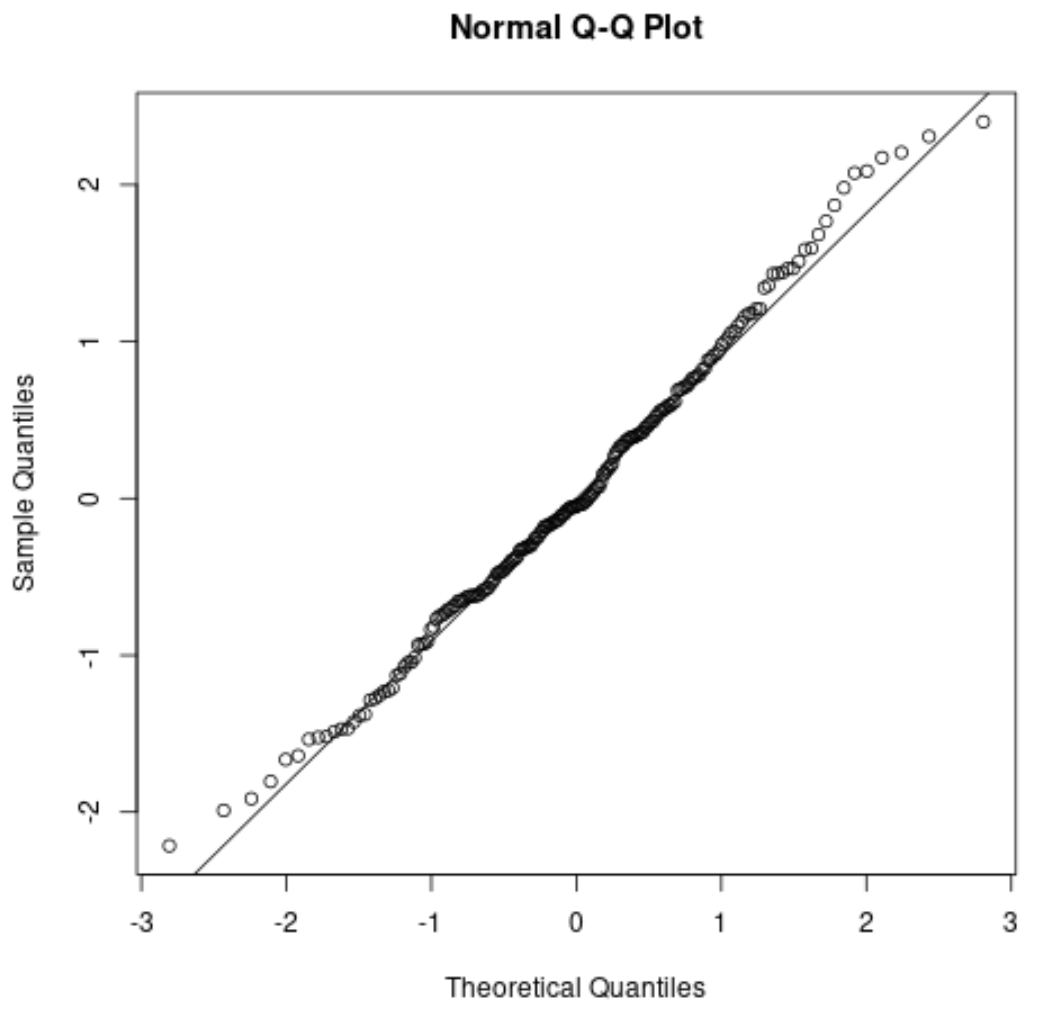
အကြံပြုချက်များသည် အမြီးစွန်းရှိ ဖြောင့်ထောင့်ဖြတ်မျဉ်းမှ အနည်းငယ်သွေဖည်သွားသော်လည်း ယေဘုယျအားဖြင့် အကြံပြုချက်များသည် ထောင့်ဖြတ်မျဉ်းအတိုင်း ကောင်းစွာကျသည်။ ဒါက ပုံမှန်ဖြစ်ရိုးဖြစ်စဉ် ယူဆချက်နဲ့ ကိုက်ညီတယ်လို့ ကျွန်တော်တို့ကို ပြောပြတယ်။
အကိုးအကားအတွက်၊ ဤသည်မှာ ပုံမှန်မဟုတ်သော ဖြန့်ဝေခြင်းမဟုတ်သော အကြွင်းအကျန်များအတွက် QQ ကွက်ကွက်ကဲ့သို့ ဖြစ်ကောင်းဖြစ်နိုင်သည်-
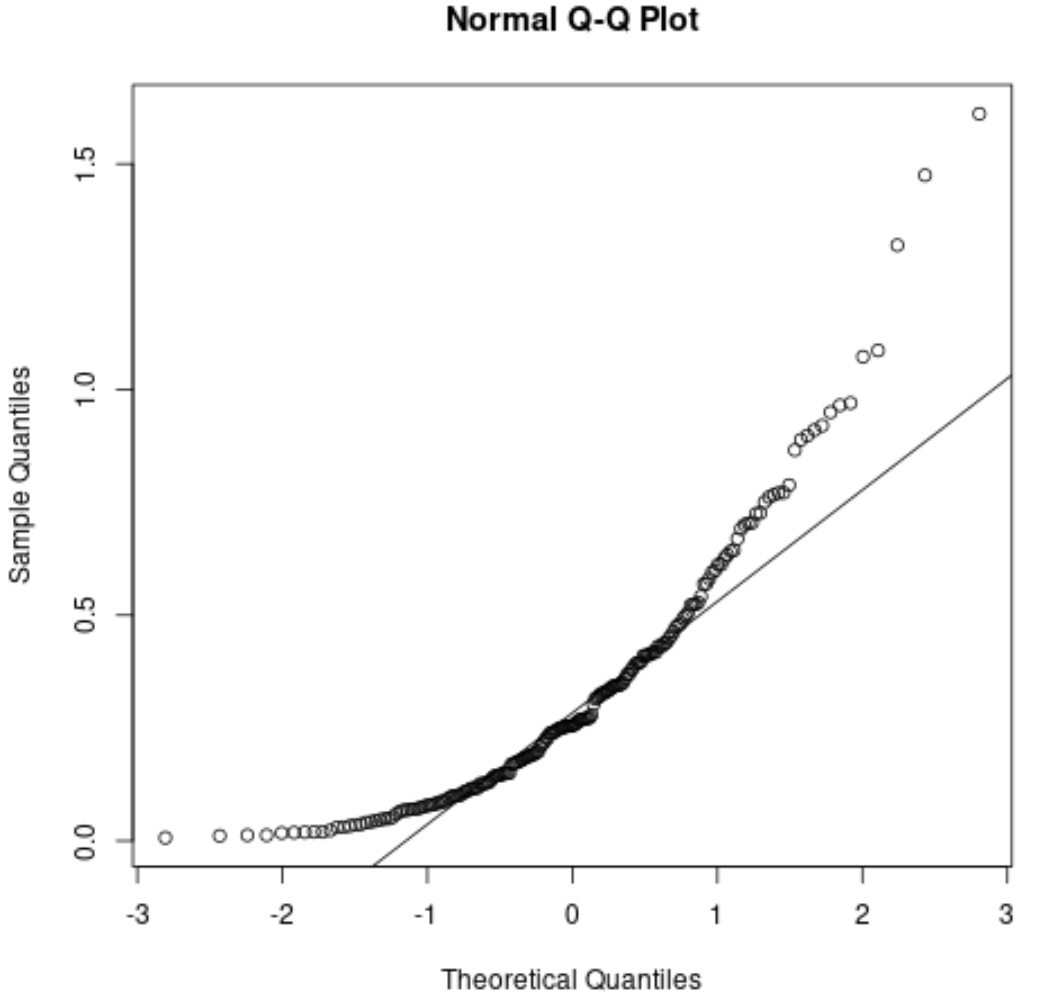
အကြွင်းအကျန်များကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်းမရှိကြောင်း ညွှန်ပြသော ဖြောင့်ထောင့်ဖြတ်မျဉ်းမှ အမှတ်များသည် အလွန်သွေဖည်သွားပါသည်။
မတူညီသောဆော့ဖ်ဝဲလ်တွင် QQကွက်များကိုဖန်တီးနည်းကိုလေ့လာရန် အောက်ပါသင်ခန်းစာများကို ကိုးကားပါ။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ပါဆောင်းပါးများသည် ANOVA မော်ဒယ်များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-
One-Way ANOVA မိတ်ဆက်
ANOVA ယူဆချက်များကို စစ်ဆေးနည်း
လက်တွေ့ဘဝတွင် ANOVA အသုံးပြုခြင်း၏ ဥပမာ 4 ခု
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။