Python တွင် augmented dickey-fuller စမ်းသပ်မှု (ဥပမာနှင့်အတူ)

အချိန်စီးရီးတစ်ခုသည် ခေတ်ရေစီးကြောင်းမရှိပါက၊ အချိန်နှင့်အမျှ အဆက်မပြတ်ကွဲလွဲမှုကိုတင်ပြပြီး အချိန်နှင့်အမျှ ဆက်တိုက်အလိုအလျောက်ဆက်နွှယ်မှုဖွဲ့စည်းပုံပါရှိသည့် အချိန်စီးရီးတစ်ခုအား “ စာရေးကိရိယာ” ဟု ဆိုပါသည်။

အချိန်စီးရီးတစ်ခုသည် တည်ငြိမ်မှုရှိမရှိ စမ်းသပ်ရန် နည်းလမ်းတစ်ခုမှာ အောက်ပါ null နှင့် အခြားအခြားသော ယူဆချက်များကို အသုံးပြုထားသည့် augmented Dickey-Fuller စမ်းသပ်မှုကို လုပ်ဆောင်ရန်ဖြစ်သည်-

H ₀ : အချိန်စီးရီးသည် လှုပ်ရှားမှုမရှိပေ။ တစ်နည်းဆိုရသော် ၎င်း၏ဖွဲ့စည်းပုံသည် အချိန်ပေါ်မူတည်ပြီး ၎င်း၏ပြောင်းလဲမှုသည် အချိန်နှင့်အမျှ မတည်မြဲပါ။

H _A : အချိန်စီးရီးသည် ငြိမ်သက်နေသည်။

အကယ်၍ စမ်းသပ်မှု၏ p-တန်ဖိုး သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက (ဥပမာ α = 0.05)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်ပြီး time series သည် ငြိမ်နေသည်ဟု ကောက်ချက်ချနိုင်ပါသည်။

အောက်ပါ အဆင့်ဆင့် ဥပမာသည် ပေးထားသော အချိန်စီးရီးအတွက် Python တွင် တိုးမြှင့်ထားသော Dickey-Fuller စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

ဥပမာ- Python ရှိ Dickey-Fuller စမ်းသပ်မှုကို တိုးမြှင့်ထားသည်။

Python တွင် အောက်ပါ time series data ရှိသည်ဆိုပါစို့။

 data = [3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10]

ဒေတာအပေါ် တိုးမြှင့်ထားသော Dickey-Fuller စမ်းသပ်မှု မလုပ်ဆောင်မီ၊ ကျွန်ုပ်တို့သည် ဒေတာကို မြင်ယောင်နိုင်ရန် အမြန်ကွက်ကွက်တစ်ခုကို ဖန်တီးနိုင်သည်-

 import matplotlib. pyplot as plt

plt. plot (data) 

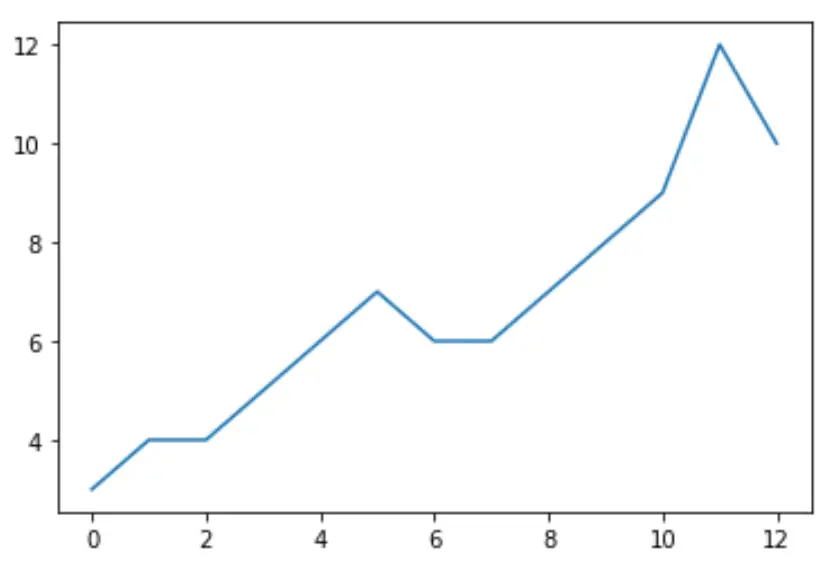
တိုးမြှင့်ထားသော Dickey-Fuller စမ်းသပ်မှုကို လုပ်ဆောင်ရန်၊ ကျွန်ုပ်တို့သည် statsmodels စာကြည့်တိုက်မှ adfuller() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။ ပထမဦးစွာ၊ ကျွန်ုပ်တို့သည် statsmodels ကိုထည့်သွင်းရန်လိုအပ်သည်-

 pip install statsmodels

ထို့နောက် ကျွန်ုပ်တို့သည် augmented Dickey-Fuller စမ်းသပ်မှုကို လုပ်ဆောင်ရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 from statsmodels. tsa . stattools import adfuller

#perform augmented Dickey-Fuller test
adfuller(data)

(-0.9753836234744063,
 0.7621363564361013,
 0,
 12,
 {'1%': -4.137829282407408,
  '5%': -3.1549724074074077,
  '10%': -2.7144769444444443},
 31.2466098872313)

ဤသည်မှာ ရလဒ်၏ အရေးကြီးဆုံးတန်ဖိုးများကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည် ။

• စမ်းသပ်စာရင်းအင်း- 0.97538
• P-တန်ဖိုး- 0.7621

p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။

ဆိုလိုသည်မှာ အချိန်စီးရီးသည် ငုတ်တုတ်မဟုတ်ပါ။ တစ်နည်းဆိုရသော် ၎င်း၏ဖွဲ့စည်းပုံသည် အချိန်ပေါ်မူတည်ပြီး ၎င်း၏ပြောင်းလဲမှုသည် အချိန်နှင့်အမျှ မတည်မြဲပါ။

ထပ်လောင်းအရင်းအမြစ်များ

Matplotlib တွင် အချိန်စီးရီးတစ်ခုကို ဘယ်လိုဆွဲမလဲ။
Pandas DataFrame မှ စီးရီးများစွာကို ဘယ်လိုဆွဲမလဲ။
Python တွင် Mann-Kendall Trend Test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။