နှိုင်းယှဉ်မှုများစွာအတွက် dunnett ၏စမ်းသပ်မှုကို အသုံးပြုနည်း

ANOVA (ကွဲလွဲမှုကို ခွဲခြမ်းစိတ်ဖြာခြင်း) ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော သီးခြားအုပ်စုများ၏ နည်းလမ်းများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ANOVA ၏ p-value သည် သတ်မှတ်ထားသော အရေးကြီးသော အဆင့်တစ်ခုအောက်တွင် ရှိနေပါက၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး အနည်းဆုံး အုပ်စု၏ ဆိုလိုသည်မှာ အခြားနည်းလမ်းများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား ရှိသည်ဟု ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်ပါသည် ။

သို့သော် မည်သည့် အဖွဲ့များ အချင်းချင်း ကွဲပြားသည်ကို ဤအရာက ကျွန်ုပ်တို့အား မပြောပါ။ ၎င်းသည် ကျွန်ုပ်တို့အား အုပ်စု ပျမ်းမျှ ပျမ်းမျှအားလုံး မညီမျှကြောင်း ရိုးရှင်းစွာ ပြောပြသည်။ ဘယ်အဖွဲ့တွေက တစ်ယောက်နဲ့တစ်ယောက် မတူဘူးဆိုတာ အတိအကျသိဖို့အတွက် Post-hoc test လုပ်ဖို့လိုပါတယ်။

လေ့လာမှုရှိအုပ်စုတစ်စုကို ထိန်းချုပ်ရေးအဖွဲ့ ဟုယူဆပါက၊ ANOVA ပြီးနောက် Dunnett ၏စမ်းသပ်မှုကို post-hoc စမ်းသပ်မှုအဖြစ် ကျွန်ုပ်တို့အသုံးပြုသင့်သည်။

Dunnett စမ်းသပ်မှု: အဓိပ္ပါယ်

Dunnett စမ်းသပ်မှုကို လုပ်ဆောင်ရန် အောက်ပါ အဆင့်နှစ်ဆင့်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

အဆင့် 1- Dunnett ၏အရေးပါသောတန်ဖိုးကိုရှာပါ။

ဦးစွာ၊ ကျွန်ုပ်တို့သည် Dunnett ၏ အရေးပါသောတန်ဖိုးကို ရှာဖွေရန် လိုအပ်သည်။ ၎င်းကို အောက်ပါအတိုင်း တွက်ချက်သည်။

Dunnett အရေးပါသောတန်ဖိုး- t _d √ 2MS _w /n

ရွှေ-

• t _d : ပေးထားသော အယ်လ်ဖာအဆင့်၊ အုပ်စုအရေအတွက်နှင့် အုပ်စုနမူနာအရွယ်အစားများအတွက် Dunnett ၏ဇယား တွင်တွေ့ရသောတန်ဖိုး။
• MS _w : ANOVA အထွက်ဇယားရှိ “အုပ်စုအတွင်း” ၏ ပျမ်းမျှစတုရန်းများ
• n- အုပ်စုနမူနာအရွယ်အစား

အဆင့် 2- Dunnett ၏ အရေးပါသောတန်ဖိုးနှင့် အုပ်စုနည်းလမ်းများကြား ကွာခြားချက်များကို နှိုင်းယှဉ်ပါ။

ထို့နောက်၊ အုပ်စုတစ်ခုစီ၏ပျမ်းမျှနှင့်ထိန်းချုပ်မှုအုပ်စု၏ပျမ်းမျှအကြားအကြွင်းမဲ့ခြားနားချက်ကိုတွက်ချက်သည်။ ကွာခြားချက်သည် Dunnett ၏ အရေးပါသောတန်ဖိုးထက် ကျော်လွန်ပါက၊ ဤကွာခြားချက်ကို ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်ဟု ဆိုပါသည်။

အောက်ဖော်ပြပါ ဥပမာသည် Dunnett စာမေးပွဲကို လက်တွေ့တွင် မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

Dunnett စမ်းသပ်မှု- ဥပမာ

လေ့လာမှုအသစ်နှစ်ခုသည် ကျောင်းသားများ၏ စာမေးပွဲရမှတ်များကို တိုးတက်စေမည့် အလားအလာရှိမရှိ ဆရာတစ်ဦးမှ သိချင်သည်ဆိုပါစို့။ ၎င်းကိုစမ်းသပ်ရန်၊ သူမ၏အတန်းတွင် ကျောင်းသား 30 ကို အောက်ဖော်ပြပါ အုပ်စုသုံးစုဖြင့် ကျပန်းခွဲသည်။

• ထိန်းချုပ်ရေးအဖွဲ့- ကျောင်းသား ၁၀ ဦး
• နည်းပညာလေ့လာမှုအသစ် 1: 10 ကျောင်းသား
• နည်းပညာလေ့လာမှုအသစ် 2: 10 ကျောင်းသား

၎င်းတို့၏ သတ်မှတ်ထားသော လေ့လာမှုနည်းစနစ်ကို အသုံးပြုပြီး တစ်ပတ်အကြာတွင် ကျောင်းသားတစ်ဦးစီသည် တူညီသောစာမေးပွဲကို ဖြေဆိုကြသည်။ ရလဒ်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

• ထိန်းချုပ်မှုအဖွဲ့၏ ပျမ်းမျှစာမေးပွဲရမှတ်- 81.6
• လေ့လာမှုနည်းပညာအုပ်စုအသစ်အတွက် ပျမ်းမျှစာမေးပွဲရမှတ် 1: 85.8
• New Study Technique 2 အုပ်စုစာမေးပွဲတွင် ပျမ်းမျှရမှတ်- 87.7
• ANOVA အထွက်ဇယားရှိ “အုပ်စုအတွင်း” ၏ ပျမ်းမျှစတုရန်းများ- 23.3

ဤအချက်အလက်ဖြင့်၊ လေ့လာမှုအသစ်နှစ်ခုမှတစ်ခုသည် ထိန်းချုပ်မှုအဖွဲ့ထက် သိသိသာသာကွဲပြားသောပျမ်းမျှစာမေးပွဲရမှတ်များကိုထုတ်ပေးခြင်းရှိမရှိ ဆုံးဖြတ်ရန် Dunnett စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်။

အဆင့် 1- Dunnett ၏အရေးပါသောတန်ဖိုးကိုရှာပါ။

α = 0.05၊ အုပ်စုနမူနာအရွယ်အစား n = 10၊ နှင့် အုပ်စုစုစုပေါင်း = 3 ကိုအသုံးပြု၍ Dunnett ၏ဇယားသည် အရေးပါသောတန်ဖိုးကိုတွက်ချက်ရာတွင် 2.57 တန်ဖိုးကို အသုံးပြုရန် ကျွန်ုပ်တို့အား ပြောထားသည်။

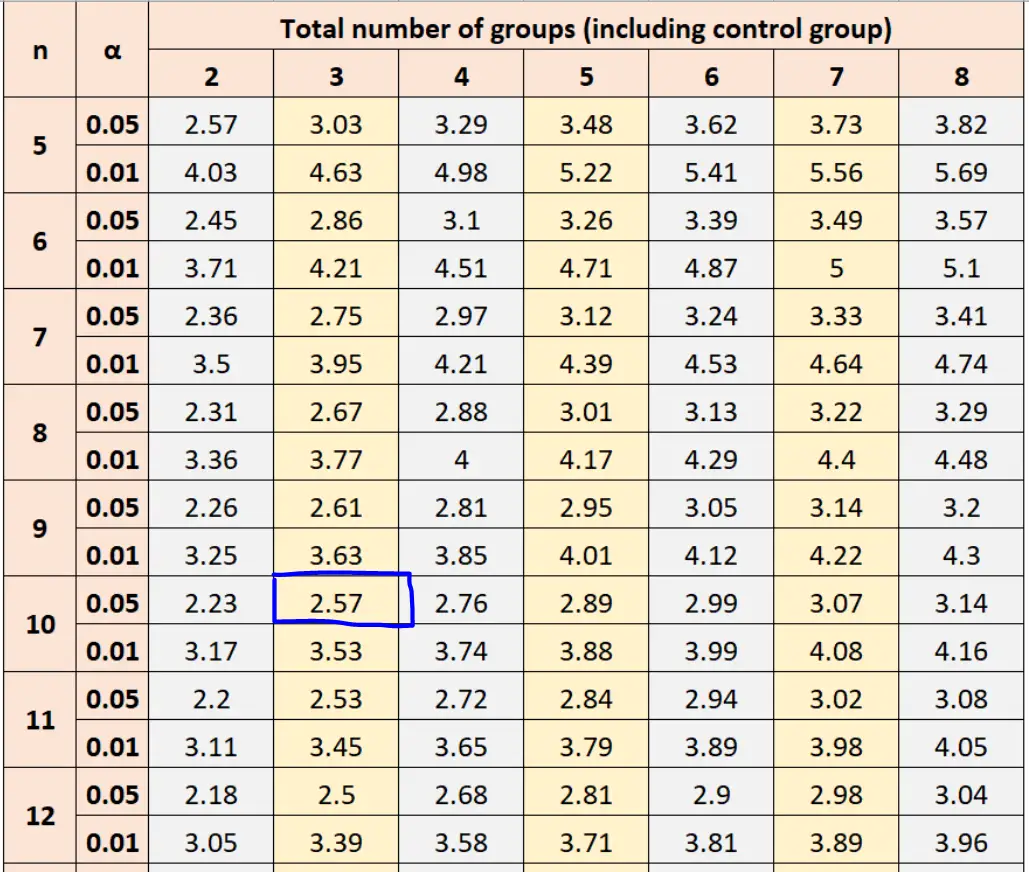
ထို့နောက် အရေးကြီးသော Dunnett တန်ဖိုးကို ရှာဖွေရန် ဤနံပါတ်ကို ဖော်မြူလာတွင် ထည့်သွင်းနိုင်သည်-

Dunnett ၏ အရေးပါသောတန်ဖိုး- t _d √ 2MS _w /n = 2.57√ 2(23.3)/10 = 5.548

အဆင့် 2- Dunnett ၏ အရေးပါသောတန်ဖိုးနှင့် အုပ်စုနည်းလမ်းများကြား ကွာခြားချက်များကို နှိုင်းယှဉ်ပါ။

လေ့လာမှုနည်းပညာတစ်ခုစီ၏နည်းလမ်းများနှင့် ထိန်းချုပ်မှုအဖွဲ့၏အကြွင်းမဲ့ကွာခြားချက်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

• ဗိုက်သား။ နည်းပညာအသစ် 1 နှင့် ထိန်းချုပ်မှုကြား ကွာခြားချက်- |85.8 – 81.6| = ၄.၂
• ဗိုက်သား။ နည်းပညာအသစ် 2 နှင့် ထိန်းချုပ်မှုကြား ကွာခြားချက်- |87.7 – 81.6| = ၆.၁

နည်းပညာ 2 နှင့် ထိန်းချုပ်မှုအုပ်စုကြားရှိ ပကတိကွာခြားချက်သာလျှင် 5,548 ၏ Dunnett အရေးပါသောတန်ဖိုးထက် ကြီးသည်။

ထို့ကြောင့်၊ လေ့လာမှုနည်းပညာအသစ် #2 သည် ထိန်းချုပ်မှုအဖွဲ့နှင့် နှိုင်းယှဉ်ပါက သိသိသာသာကွဲပြားသော စာမေးပွဲရလဒ်များကို ထုတ်ပေးသည်ဟု ကျွန်ုပ်တို့ပြောနိုင်သည်၊ သို့သော် ၎င်းသည် လေ့လာမှုနည်းပညာအသစ် #1 အတွက် ကိစ္စမဟုတ်ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

One-Way ANOVA မိတ်ဆက်
ANOVA ဖြင့် Post-Hoc Testing ကိုအသုံးပြုခြင်းလမ်းညွှန်
R တွင် Dunnett ၏စမ်းသပ်မှုကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။