R တွင် dunnett ၏စမ်းသပ်မှုကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။
Post hoc test သည် မည်သည့်အဖွဲ့၏ အဓိပ္ပါယ်သည် တစ်ခုနှင့်တစ်ခု ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာ ကွာခြားသည်ကို ဆုံးဖြတ်ရန် ANOVA ပြီးနောက် လုပ်ဆောင်သော စမ်းသပ်မှုအမျိုးအစားတစ်ခုဖြစ်သည်။
လေ့လာမှုအုပ်စုများထဲမှ တစ်ခုကို ထိန်းချုပ်ရေးအဖွဲ့ ဟု ယူဆပါက၊ ကျွန်ုပ်တို့သည် Dunnett ၏စမ်းသပ်မှုကို post-hoc စမ်းသပ်မှုအဖြစ် အသုံးပြုသင့်သည်။
ဤသင်ခန်းစာတွင် Dunnett စာမေးပွဲကို R တွင် မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။
ဥပမာ- R တွင် Dunnett စမ်းသပ်မှု
လေ့လာမှုအသစ်နှစ်ခုသည် ကျောင်းသားများ၏ စာမေးပွဲရမှတ်များကို တိုးတက်စေမည့် အလားအလာရှိမရှိ ဆရာတစ်ဦးမှ သိချင်သည်ဆိုပါစို့။ ၎င်းကိုစမ်းသပ်ရန်၊ သူမ၏အတန်းတွင် ကျောင်းသား 30 ကို အောက်ဖော်ပြပါ အုပ်စုသုံးစုဖြင့် ကျပန်းခွဲသည်။
- ထိန်းချုပ်ရေးအဖွဲ့- ကျောင်းသား ၁၀ ဦး
- နည်းပညာလေ့လာမှုအသစ် 1: 10 ကျောင်းသား
- နည်းပညာလေ့လာမှုအသစ် 2: 10 ကျောင်းသား
၎င်းတို့၏ သတ်မှတ်ထားသော လေ့လာမှုနည်းစနစ်ကို အသုံးပြုပြီး တစ်ပတ်အကြာတွင် ကျောင်းသားတစ်ဦးစီသည် တူညီသောစာမေးပွဲကို ဖြေဆိုကြသည်။
ဒေတာအတွဲတစ်ခုဖန်တီးရန်၊ အုပ်စု၏နည်းလမ်းကိုမြင်ယောင်ရန်၊ တစ်ကြောင်း ANOVA လုပ်ဆောင်ရန်နှင့် နောက်ဆုံးတွင် မည်သည့်လေ့လာမှုနည်းပညာအသစ် (ရှိပါက) သည် ထိန်းချုပ်မှုအဖွဲ့နှင့် နှိုင်းယှဉ်ခြင်းဖြင့် ကွဲပြားသောရလဒ်များကိုထုတ်ပေးကြောင်း ဆုံးဖြတ်ရန် R တွင် အောက်ပါအဆင့်များကို ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။ .
အဆင့် 1: ဒေတာအတွဲကို ဖန်တီးပါ။
အောက်ပါကုဒ်သည် ကျောင်းသား 30 ဦးလုံး၏ စာမေးပွဲရလဒ်များပါရှိသော ဒေတာအတွဲတစ်ခုကို ဖန်တီးနည်းကို ပြသသည်-
#create data frame data <- data.frame(technique = rep (c("control", "new1", "new2"), each = 10 ), score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89, 81, 82, 83, 83, 83, 84, 87, 90, 92, 93, 77, 78, 79, 88, 89, 90, 91, 95, 95, 98)) #view first six rows of data frame head(data) technical score 1 control 76 2 controls 77 3 controls 77 4 controls 81 5 controls 82 6 controls 82
အဆင့် 2- အုပ်စုတစ်ခုစီအတွက် စာမေးပွဲရလဒ်များကို ကြည့်ပါ။
အုပ်စုတစ်ခုစီအတွက် စာမေးပွဲရလဒ်များ ဖြန့်ဝေမှုကို မြင်သာစေရန် boxplots များကို မည်သို့ထုတ်လုပ်ရမည်ကို အောက်ပါကုဒ်တွင် ပြသသည်-
boxplot(score ~ technique,
data = data,
main = "Exam Scores by Studying Technique",
xlab = "Studying Technique",
ylab = "Exam Scores",
col = "steelblue",
border = "black")
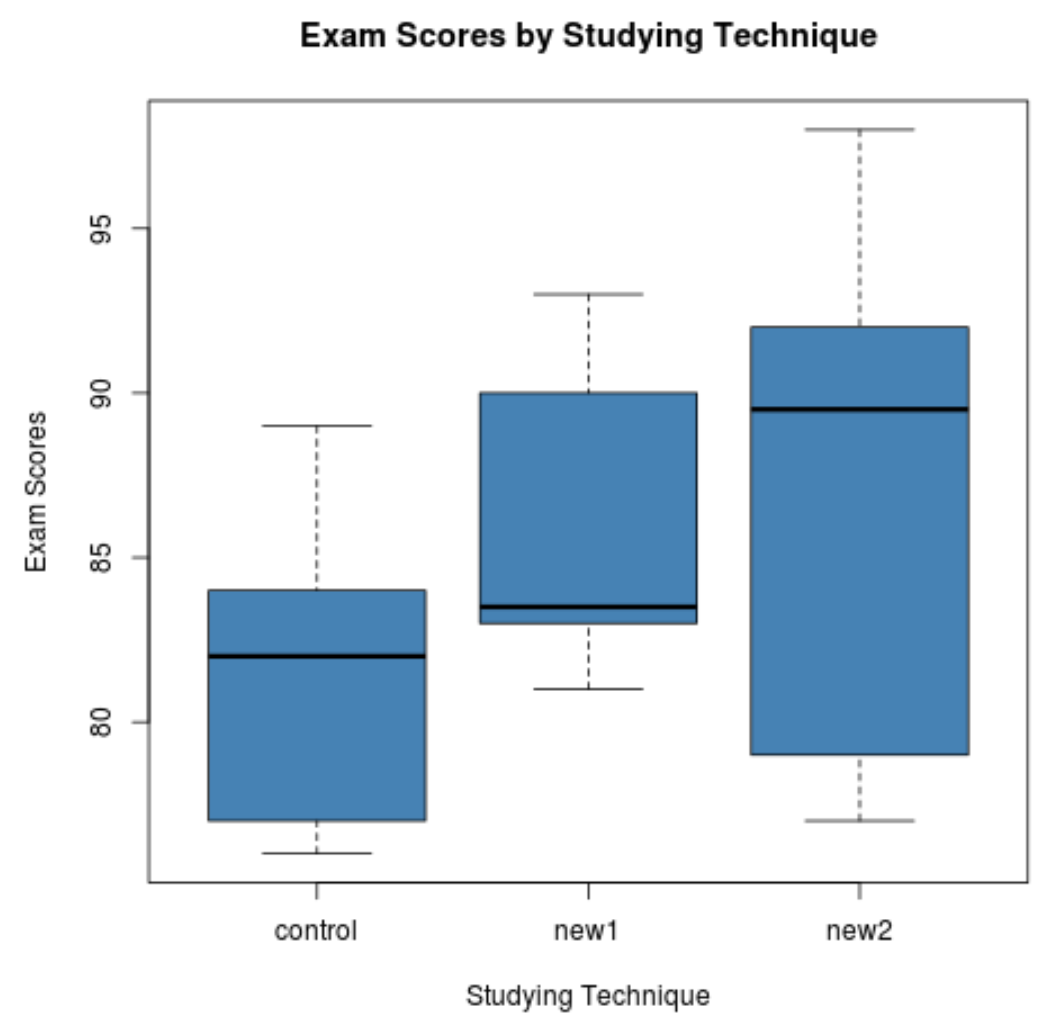
အကွက်ကွက်များမှနေ၍ စာမေးပွဲရမှတ်များ ခွဲဝေမှုသည် လေ့လာမှုနည်းပညာတစ်ခုစီအတွက် အလွန်ကွာခြားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ ထို့နောက် ဤကွဲပြားမှုများသည် စာရင်းအင်းအရ သိသာထင်ရှားမှုရှိမရှိ ဆုံးဖြတ်ရန် တစ်လမ်းသွား ANOVA ကို လုပ်ဆောင်ပါမည်။
ဆက်စပ်- R ဖြင့် ဇယားကွက်တစ်ခုတွင် Multiple Box Plot များကို မည်သို့ဆွဲမည်နည်း။
အဆင့် 3- တစ်လမ်းမောင်း ANOVA လုပ်ဆောင်ပါ။
အုပ်စုတစ်ခုစီရှိ ပျမ်းမျှစာမေးပွဲရမှတ်များကြား မတူညီမှုများကို စမ်းသပ်ရန်အတွက် အောက်ပါကုဒ်သည် တစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-
#fit the one-way ANOVA model model <- aov(score ~ technique, data = data) #view model output summary(model) Df Sum Sq Mean Sq F value Pr(>F) technical 2 211.5 105.73 3.415 0.0476 * Residuals 27 836.0 30.96 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
အလုံးစုံ p-တန်ဖိုး ( 0.0476 ) သည် 0.05 ထက်နည်းသောကြောင့်၊ အုပ်စုတစ်ခုစီတွင် တူညီသောပျမ်းမျှစာမေးပွဲရမှတ်မရှိခြင်းကို ညွှန်ပြသည်။ ထို့နောက်၊ ထိန်းချုပ်မှုအဖွဲ့မှ ကွာခြားသည့် ပျမ်းမျှစာမေးပွဲရမှတ်များကို မည်သည့်လေ့လာမှုနည်းပညာမှထုတ်ပေးသည်ကို ဆုံးဖြတ်ရန် Dunnett စာမေးပွဲကို ကျွန်ုပ်တို့လုပ်ဆောင်ပါမည်။
အဆင့် 4: Dunnett စမ်းသပ်မှုကိုလုပ်ဆောင်ပါ။
R တွင် Dunnett စမ်းသပ်မှုကို လုပ်ဆောင်ရန် အောက်ပါ syntax ကိုအသုံးပြုသည့် DescTools စာကြည့်တိုက်မှ DunnettTest() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်ပါသည်။
Dunnett စမ်းသပ်မှု(x၊ g)
ရွှေ-
- x- ဒေတာတန်ဖိုးများ၏ ကိန်းဂဏာန်း vector တစ်ခု (ဥပမာ စာမေးပွဲရလဒ်များ)
- g- အုပ်စုများ၏အမည်များကိုသတ်မှတ်ပေးသော vector တစ်ခု (ဥပမာ-လေ့လာမှုနည်းပညာ)
အောက်ပါကုဒ်သည် ကျွန်ုပ်တို့၏ ဥပမာအတွက် ဤလုပ်ဆောင်ချက်ကို အသုံးပြုနည်းကို ပြသသည်-
#load DescTools library library(DescTools) #perform Dunnett's Test DunnettTest(x=data$score, g=data$technique) Dunnett's test for comparing several treatments with a control: 95% family-wise confidence level $control diff lwr.ci upr.ci pval new1-control 4.2 -1.6071876 10.00719 0.1787 new2-control 6.4 0.5928124 12.20719 0.0296 * --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1' '1.' 0.1 ' ' 1
ရလဒ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် နည်းလမ်းမှာ အောက်ပါအတိုင်းဖြစ်သည်။
- လေ့လာမှုနည်းလမ်းသစ် 1 နှင့် ထိန်းချုပ်မှုအဖွဲ့ကြား စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှကွာခြားချက်မှာ 4.2 ဖြစ်သည်။ သက်ဆိုင်ရာ p-value သည် 0.1787 ဖြစ်သည်။
- လေ့လာမှုနည်းလမ်းသစ် 2 နှင့် ထိန်းချုပ်မှုအဖွဲ့ကြား စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှကွာခြားချက်မှာ 6.4 ဖြစ်သည်။ သက်ဆိုင်ရာ p-တန်ဖိုးသည် 0.0296 ဖြစ်သည်။
ရလဒ်များအပေါ် အခြေခံ၍ Technique 2 ကိုလေ့လာခြင်းသည် ထိန်းချုပ်မှုအဖွဲ့နှင့် သိသိသာသာ (p = 0.0296) ကွာခြားသည့် ပျမ်းမျှစာမေးပွဲရမှတ်များကို ထုတ်ပေးသည့် တစ်ခုတည်းသောနည်းလမ်းဖြစ်ကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။
ထပ်လောင်းအရင်းအမြစ်များ
One-Way ANOVA မိတ်ဆက်
တစ်လမ်းမောင်း ANOVA ကို R ဖြင့် မည်သို့လုပ်ဆောင်ရမည်နည်း။
R တွင် Tukey စမ်းသပ်မှုပြုလုပ်နည်း