ပင်ကိုယ်ဖြစ်နိုင်ခြေ

ဤဆောင်းပါးတွင် empirical probability တွက်ချက်နည်းကို ရှင်းပြထားပါသည်။ empirical probability ကဘာလဲ၊ သူ့ရဲ့ဖော်မြူလာကဘာလဲ၊ ဥပမာတစ်ခုနဲ့ empirical probability နဲ့ သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေကြားက ကွာခြားချက်တွေက ဘာတွေလဲဆိုတာ သင်ရှာဖွေတွေ့ရှိပါလိမ့်မယ်။

empirical probability ဆိုတာ ဘာလဲ။

Empirical probability သည် အဖြစ်အပျက်တစ်ခု ဖြစ်ပွားနိုင်ခြေကို ညွှန်ပြသော empirical tests သို့မဟုတ် facts များအပေါ် အခြေခံ၍ ကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှုတစ်ခုဖြစ်သည်။

တစ်နည်းဆိုရသော်၊ စမ်းသပ်မှုတစ်ခု၏ရလဒ်များမှ empirical probability ကိုတွက်ချက်ပြီး အဖြစ်အပျက်တစ်ခုဖြစ်ပေါ်လာနိုင်ခြေကိုပြောပြသည်။

စမ်းသပ်မှုကို ထပ်ခါထပ်ခါ ပြုလုပ်လေ၊ ရရှိသော ပင်ကိုယ်ဖြစ်နိုင်ခြေ တိကျလေလေဖြစ်သည်။ အဘယ်ကြောင့်ဆိုသော် ဤဖြစ်နိုင်ခြေအမျိုးအစားသည် အကြိမ်ပေါင်းထောင်ပေါင်းများစွာကို အတုယူကာ အချိန်တိုအတွင်း ခွဲခြမ်းစိတ်ဖြာနိုင်သော ကွန်ပျူတာပရိုဂရမ်များကို အသုံးပြု၍ ဆုံးဖြတ်လေ့ရှိပါသည်။

Empirical probability သည် 0 နှင့် 1 အကြား ဂဏန်းတစ်ခုဖြစ်သည်။ ဖြစ်ရပ်တစ်ခု ဖြစ်ပွားရန် အလားအလာ ပိုများလေ၊ empirical probability ပိုများလေ၊ နှင့် အပြန်အလှန်အားဖြင့်၊ ဖြစ်ရပ်တစ်ခု ဖြစ်ပွားနိုင်ခြေနည်းလေ၊ ၎င်း၏ empirical probability နည်းပါးလေဖြစ်သည်။

Empirical ဖြစ်နိုင်ခြေ ဖော်မြူလာ

ယေဘူယျဖြစ်နိုင်ခြေအတွက် ဖော်မြူလာ သည် စမ်းသပ်မှုတစ်ခုအတွင်း အဖြစ်အပျက်တစ်ခုဖြစ်ပွားသည့်အကြိမ်အရေအတွက်ဖြစ်ပြီး စမ်းသပ်မှုပြုလုပ်ခဲ့သည့် အကြိမ်စုစုပေါင်းကို ပိုင်းခြားထားသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် သစ်ပင်တစ်ပင်ကို ဆယ်ကြိမ်ကြည့်ရှုပြီး သစ်ပင်၌ ငှက်တစ်ကောင်ကို ခုနစ်ကြိမ်တွေ့ဖူးပါက၊ သစ်ပင်ကိုကြည့်ရင်း ငှက်တစ်ကောင်ကို မြင်နိုင်သည့် ပင်ကိုယ်ဖြစ်နိုင်ခြေမှာ-

Empirical Probability ၏ ဥပမာ

empirical probability ၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့် ဤဖြစ်နိုင်ခြေအမျိုးအစားအပေါ် အဆင့်ဆင့် လေ့ကျင့်ခန်းတစ်ခုကို ဖြေရှင်းပါမည်။ ဤနည်းဖြင့် သင်သည် empirical probability ကို မည်ကဲ့သို့ တွက်ချက်သည်ကို သိနိုင်သည်။

• သေခြင်းကို လှိမ့်ခြင်း၏ ကျပန်းစမ်းသပ်မှုတွင် ပါဝင်သည့် မူလဖြစ်ရပ်များ၏ ပင်ကိုယ်ဖြစ်နိုင်ခြေကို တွက်ချက်သည်။

ပထမဦးစွာ၊ ရရှိလာသော စမ်းသပ်မှုရလဒ်များကို သီအိုရီရလဒ်များနှင့် နှိုင်းယှဉ်ခြင်း၏ သီအိုရီဆိုင်ရာ ဖြစ်နိုင်ခြေကို တွက်ချက်ပါမည်။ (၁၊ ၂၊ ၃၊ ၄၊ ၅ နှင့် ၆) တွင် ဖြစ်နိုင်ခြေရှိသော ရလဒ်ခြောက်ခုရှိသည်၊ ထို့ကြောင့် မူလဖြစ်ရပ်တစ်ခုစီ၏ သီအိုရီဖြစ်နိုင်ခြေမှာ-

ဤလေ့ကျင့်ခန်းကိုဖြေရှင်းရန်၊ ကျွန်ုပ်တို့သည် သေတ္တာကို အကြိမ်များစွာ လှည့်ပတ်ကာ ရလဒ်များကို အရေးပေါ်ဇယားတွင် မှတ်တမ်းတင်ရပါမည်။ အဲဒါအတွက် ဥပမာ Excel ပရိုဂရမ်ကို သုံးနိုင်ပါတယ်။

စမ်းသပ်မှုအရေအတွက်၏ အရေးပါမှုကို သင်မြင်နိုင်စေရန်အတွက်၊ ကျွန်ုပ်တို့သည် ပထမအကြိမ် လွှတ်တင်မှု ဆယ်ခု၊ ထို့နောက် တစ်ရာနှင့် နောက်ဆုံးတွင် တစ်ထောင်ကို ပုံဖော်ပါမည်။ ထို့ကြောင့်၊ ပထမအကြိမ် ကျပန်းပစ်ခြင်း ၁၀ ခု၏ သရုပ်ဖော်မှုမှ ရရှိသော ရလဒ်များမှာ အောက်ပါအတိုင်း ဖြစ်သည်။

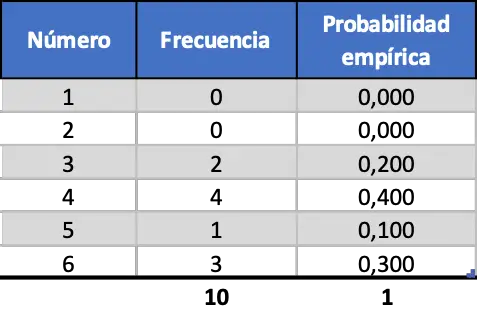
သင်တွေ့မြင်ရသည့်အတိုင်း၊ ပစ်ဆယ်ကြိမ်သာ ပုံဖော်ခြင်းဖြင့် ရရှိသော ပင်ကိုယ်ဖြစ်နိုင်ခြေများသည် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ (0.167) နှင့် မနီးစပ်ပါ။

သို့သော် ကျွန်ုပ်တို့သည် စမ်းသပ်မှုအရေအတွက်ကို တိုးလာသည်နှင့်အမျှ၊ ဤမက်ထရစ်နှစ်ခုသည် ပို၍ဆင်တူလာသည်၊ လွှတ်တင်မှု 100 ၏ သရုပ်ဖော်ပုံကိုကြည့်ပါ-

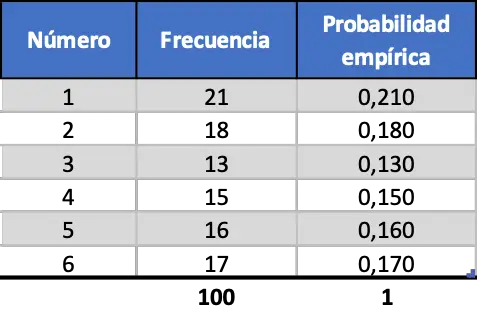
ယခုသေဆုံးမှုပေါ်ရှိ ဂဏန်းတစ်ခုစီအတွက် တွက်ချက်ထားသော empirical probability သည် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေနှင့် ပို၍ဆင်တူသော်လည်း၊ ကျွန်ုပ်တို့သည် အလွန်ကွဲပြားသောတန်ဖိုးများကို ရရှိဆဲဖြစ်သည်။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် တူညီသောလုပ်ထုံးလုပ်နည်းကို လုပ်ဆောင်သော်လည်း လွှတ်တင်မှုပေါင်း ၁၀၀၀ ကို ပုံဖော်ထားသည်။

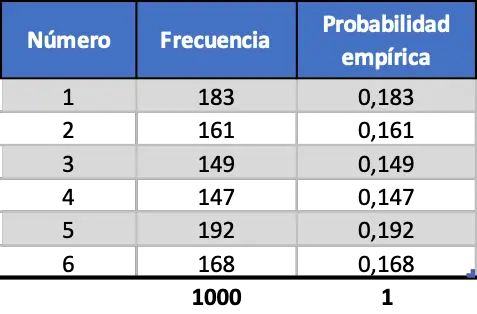
နောက်ဆုံးအခြေအနေဇယားတွင်ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်အတိုင်း၊ ယခု empirical probabilities များ၏တန်ဖိုးများသည် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေများနှင့်အလွန်နီးစပ်ပါသည်။

အချုပ်အားဖြင့် ဆိုရသော် ကျွန်ုပ်တို့သည် လက်တွေ့စမ်းသပ်မှုအရေအတွက်ကို တိုးလာလေလေ၊ အဖြစ်အပျက်တစ်ခု၏ ပင်ကိုယ်ဖြစ်နိုင်ခြေ၏တန်ဖိုးသည် ၎င်း၏သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ ဖြစ်ပျက်မှုဆီသို့ နီးကပ်လေလေဖြစ်သည်။ ဤစည်းမျဉ်းကို ကိန်းဂဏန်းများစွာ၏ ဥပဒေအဖြစ် သတ်မှတ်သည်၊ ဒေတာများများရှိလေ၊ စမ်းသပ်မှုတန်ဖိုးများသည် သီအိုရီတန်ဖိုးများနှင့် နီးကပ်လေလေဖြစ်ကြောင်း ဖော်ပြထားသည်။

ထို့အပြင်၊ ကျွန်ုပ်တို့သည် ကြိမ်နှုန်းဇယားသုံးခုကို နှိုင်းယှဉ်ပါက၊ ပင်ကိုယ်ဖြစ်နိုင်ခြေသည် အတိအကျမဟုတ်သော်လည်း လက်တွေ့စမ်းသပ်မှုအရေအတွက်ပေါ်မူတည်၍ ပြောင်းလဲသွားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်ရပါသည်။ ဆိုလိုချင်တာက သင်ရရှိထားတဲ့ တန်ဖိုးတွေကို ဘယ်လိုအဓိပ္ပာယ်ကောက်ရမယ်ဆိုတာ သိရပါမယ်။

Empirical probability နှင့် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ

နောက်ဆုံးတွင်၊ ဖြစ်နိုင်ခြေ နှစ်မျိုးရှိသော်လည်း ၎င်းတို့သည် လုံးဝကွဲပြားသော အဓိပ္ပါယ်ရှိသောကြောင့် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ၏ သဘောတရားနှင့် ဖြစ်နိုင်ခြေဆိုင်ရာ အယူအဆကို ခွဲခြမ်းစိတ်ဖြာပါမည်။

empirical probability နှင့် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေ (သို့မဟုတ် classical probability) အကြား ခြားနားချက် မှာ လက်တွေ့အတွေ့အကြုံမှ စုဆောင်းထားသော ဒေတာများမှ empirical probability ကို တွက်ချက်ပြီး သီအိုရီဆိုင်ရာ ဖြစ်နိုင်ခြေကို မည်သည့်စမ်းသပ်မှုမှ မလုပ်ဆောင်ဘဲ စံပြအခြေအနေများကို ထည့်သွင်းတွက်ချက်နေချိန်တွင် သီအိုရီဆိုင်ရာ ဖြစ်နိုင်ခြေကို တွက်ချက်ပါသည်။

ဆိုလိုသည်မှာ၊ ပင်ကိုယ်ဖြစ်နိုင်ခြေကိုရှာဖွေရန်၊ စမ်းသပ်မှုတစ်ခုအား အတုယူရမည်ဖြစ်ပြီး ရရှိသောရလဒ်များအပေါ်အခြေခံ၍ တွက်ချက်မှုကို လုပ်ဆောင်ရမည်ဖြစ်သည်။ သို့သော် သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေကို သိရန်၊ မည်သည့်စမ်းသပ်မှုမှ မလုပ်ရဘဲ သီအိုရီအရ တွက်ချက်ခြင်းသာဖြစ်သည်။

ထို့အပြင်၊ ဘက်လိုက်မှုအဆင့် ကို empirical probability နှင့် theoretical probability အကြား ခြားနားချက်အဖြစ် သတ်မှတ်သည်။ ဘက်လိုက်မှုသည် အပြုသဘော သို့မဟုတ် အနုတ်လက္ခဏာဖြစ်နိုင်သော်လည်း သုညဖြစ်ရန် အလွန်ခက်ခဲသည်၊ အကြောင်းမှာ ကျပန်းစမ်းသပ်မှုတစ်ခုသည် အလွန်ဖြစ်နိုင်ခြေရှိသော သီအိုရီဆိုင်ရာဖြစ်နိုင်ခြေကို ထိမိသွားသည်ဟု ဆိုလိုသည်။