Excel- regression coefficient အတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ပါ။

linear regression model တွင်၊ regression coefficient သည် ခန့်မှန်းသူ variable တွင် တစ်ယူနစ်တိုးခြင်းနှင့် ဆက်စပ်နေသော တုံ့ပြန်မှုကိန်းရှင် ၏ ပျမ်းမျှပြောင်းလဲမှုကို ပြောပြသည်။

ဆုတ်ယုတ်မှုကိန်းဂဏန်းအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

β ₁ အတွက် ယုံကြည်မှုကြားကာလ : b ₁ ± t _{1-α/2၊ n-2} * se(b ₁ )

ရွှေ-

•   b ₁ = Regression coefficient ကို ဆုတ်ယုတ်မှုဇယားတွင် ပြထားသည်။
• t _{1-∝/2၊ n-2} = 1-∝ ယုံကြည်မှုအဆင့်အတွက် အရေးကြီးသော t တန်ဖိုးသည် လွတ်လပ်မှု၏ n-2 ဒီဂရီဖြစ်ပြီး n သည် ကျွန်ုပ်တို့၏ဒေတာအတွဲရှိ စုစုပေါင်းကြည့်ရှုမှုအရေအတွက်ဖြစ်သည်။
• se(b ₁ ) = ဆုတ်ယုတ်မှုဇယားတွင် ပြသထားသည့် b ₁ ၏ စံအမှား

အောက်ဖော်ပြပါ ဥပမာသည် Excel တွင် ဆုတ်ယုတ်မှုကိန်းဂဏန်းအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ- Excel တွင် Regression Coefficient အတွက် Confidence Interval

အတန်းတစ်တန်းရှိ ကျောင်းသား 15 ဦးအတွက် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ခန့်မှန်းတွက်ချက်မှုကိန်းရှင်နှင့် စာမေးပွဲရမှတ်များအဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို အံကိုက်လုပ်လိုသည်ဆိုပါစို့။

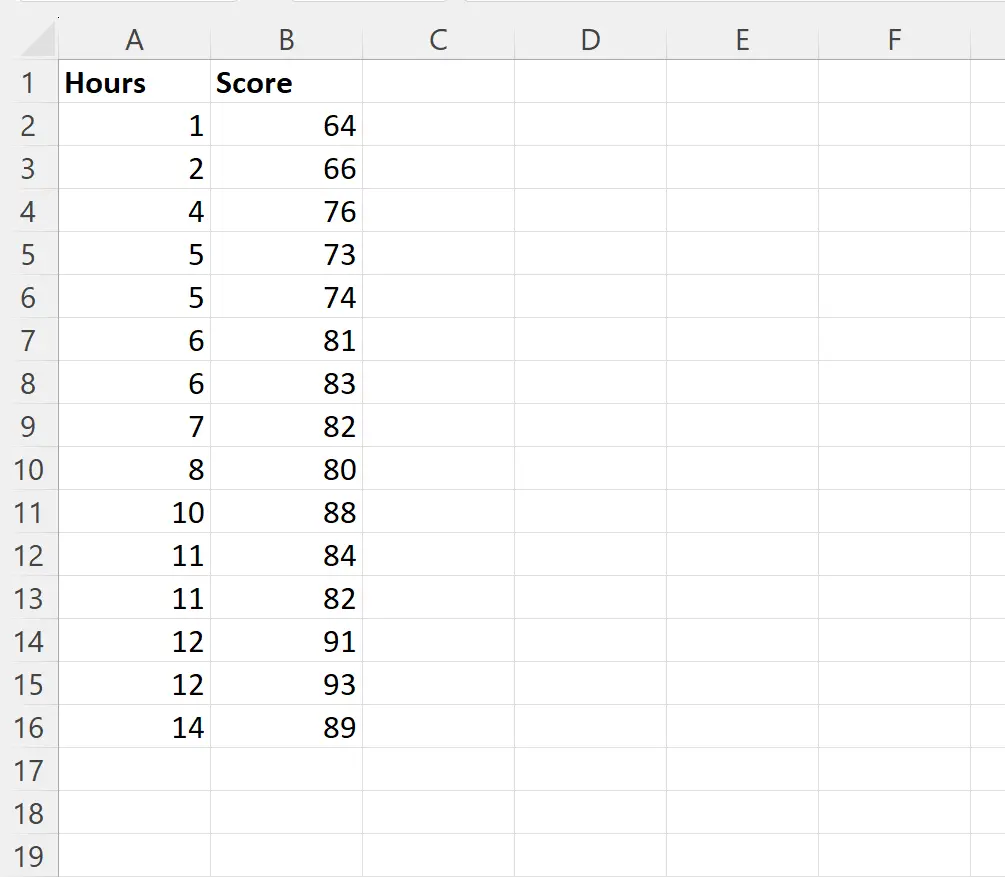
တုံ့ပြန်မှုကိန်းရှင်အဖြစ် နာရီ ကော်လံရှိ တန်ဖိုးများနှင့် ရမှတ် ကော်လံရှိ တန်ဖိုးများကို တုံ့ပြန်မှု variable အဖြစ် နာရီကော်လံရှိ တန်ဖိုးများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုလုပ်ဆောင်ရန် အောက်ပါဖော်မြူလာကို ဆဲလ် D2 တွင် ရိုက်ထည့်နိုင်သည်-

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

ပထမ TRUE အငြင်းအခုံသည် Excel အား သုညဖြစ်ရန် အတင်းအကြပ်မခိုင်းဘဲ ဆုတ်ယုတ်ခြင်းညီမျှခြင်း၏ ကြားဖြတ်ကို ပုံမှန်အတိုင်းတွက်ချက်ရန် ပြောသည်ကို သတိပြုပါ။

ဒုတိယ TRUE အငြင်းအခုံသည် ကိန်းဂဏန်းများအပြင် ကိန်းဂဏန်းများအပြင် ဆုတ်ယုတ်မှုကိန်းဂဏန်းများ ထပ်မံထုတ်လုပ်ရန် Excel အား ပြောထားသည်။

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဖော်မြူလာ၏ရလဒ်ကိုပြသသည် (အထွက်တန်ဖိုးတစ်ခုစီသည် အထွက်အောက်ရှိ အနီရောင်စာသားတွင် အဘယ်အရာကိုကိုယ်စားပြုသည်ကို ကျွန်ုပ်တို့ရှင်းပြသည်)

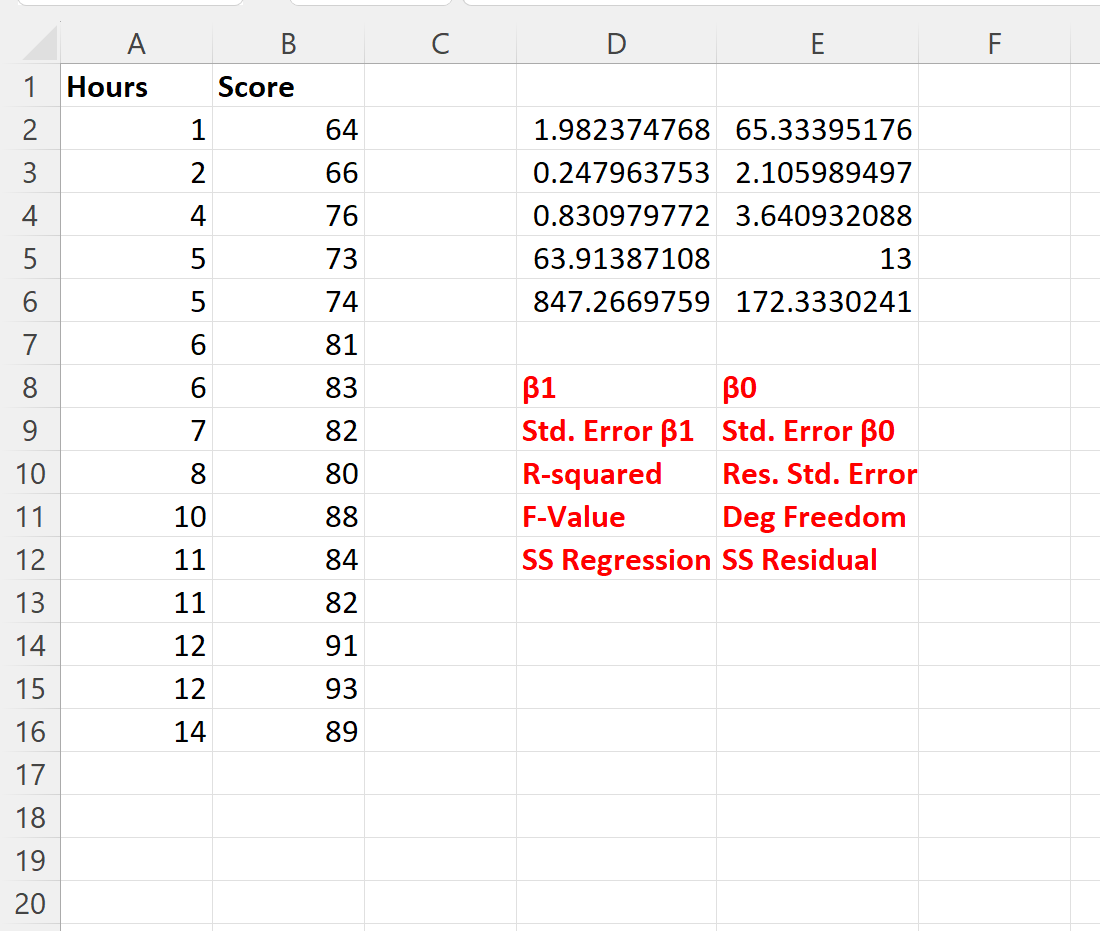
regression coefficients ကို အသုံးပြု၍ တပ်ဆင်ထားသော regression equation ကို အောက်ပါအတိုင်း ရေးသားနိုင်ပါသည်။

ရမှတ် = 65.334 + 1.982*(နာရီလေ့လာသည်)

နာရီများအတွက် regression coefficient သည် 1.982 ဖြစ်ကြောင်း သတိပြုပါ။

၎င်းသည် သင်ယူချိန် နောက်ထပ်တစ်နာရီတိုင်းသည် စာမေးပွဲရမှတ်တွင် ပျမ်းမျှ 1,982 တိုးလာခြင်းနှင့် ဆက်စပ်နေကြောင်း ၎င်းကဆိုသည်။

ဆုတ်ယုတ်မှုကိန်းဂဏန်းအတွက် 95% ယုံကြည်မှုကြားကာလကို တွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် ဆဲလ် H2 နှင့် H3 တွင် အောက်ပါဖော်မြူလာများကို ထည့်သွင်းနိုင်သည်-

• H2: = D2 – T.INV.2T(0.05၊ E5)*D3
• H3- = D2 + T.INV.2T(0.05၊ E5)*D3

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဖော်မြူလာများကို လက်တွေ့တွင် အသုံးပြုနည်းကို ပြသသည်-

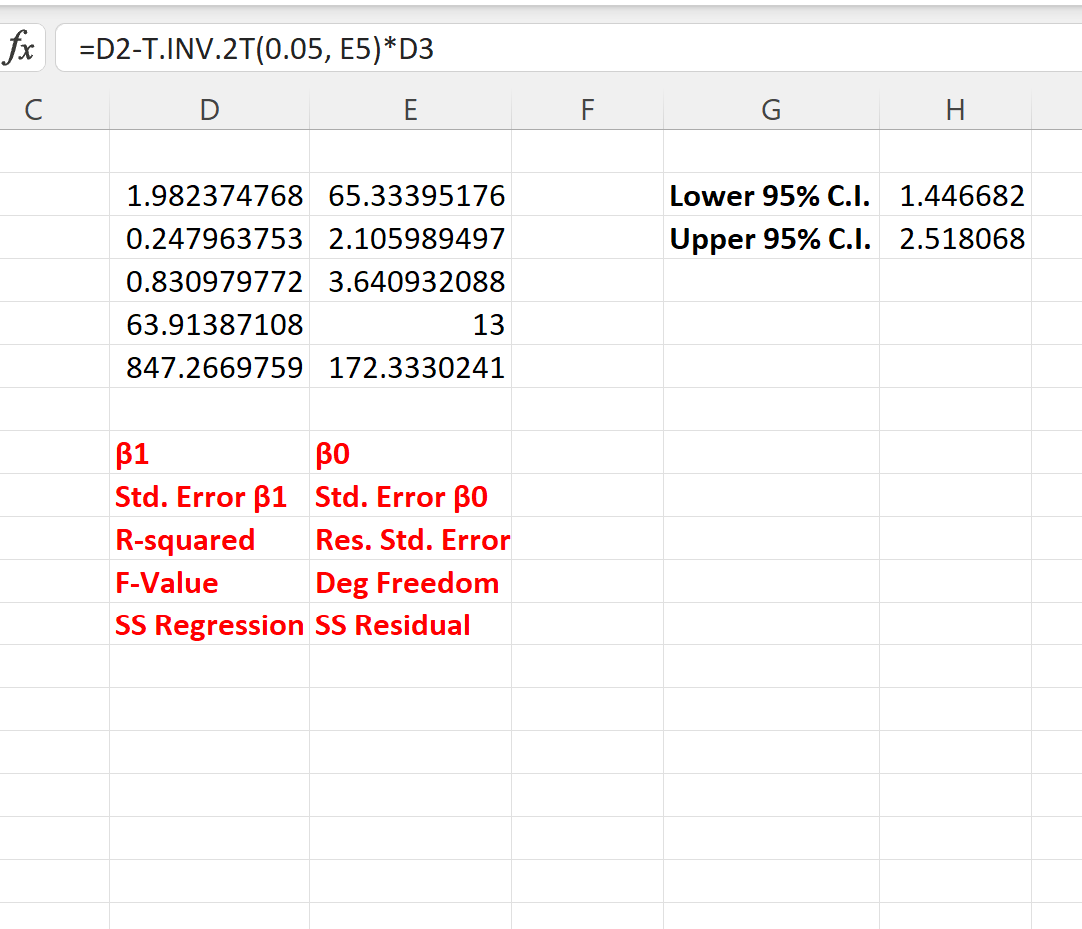
regression coefficient အတွက် 95% ယုံကြည်မှုကြားကာလသည် [1.446၊ 2.518] ဖြစ်သည်။

ဤယုံကြည်မှုကြားကာလတွင် 0 တန်ဖိုးမပါဝင်သော ကြောင့်၊ လေ့လာသည့်နာရီနှင့် စာမေးပွဲအဆင့်ကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသောဆက်စပ်မှုရှိကြောင်း ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်ပါသည်။

ဆုတ်ယုတ်မှုကိန်းဂဏန်းအတွက် 95% ယုံကြည်မှုကြားကာလကို ကိုယ်တိုင်တွက်ချက်ခြင်းဖြင့် ၎င်းသည် မှန်ကန်ကြောင်း ကျွန်ုပ်တို့လည်း အတည်ပြုနိုင်သည်-

• β ₁ အတွက် 95% CI : b ₁ ± t _{1-α/2၊ n-2} * se(b ₁ )
• β ₁ အတွက် 95% CI : 1.982 ± t _{0.975၊ 15-2} * 0.248
• β ₁ အတွက် 95% CI : 1.982 ± 2.1604 * 0.248
• β ₁ အတွက် 95% CI : [1.446၊ 2.518]

regression coefficient အတွက် 95% ယုံကြည်မှုကြားကာလသည် [1.446၊ 2.518] ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် အခြားသော အသုံးများသော အလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
Excel တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
Excel တွင် regression output တွင် P တန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံ