Excel- ဒေတာအတွဲနှစ်ခု၏ ကိန်းဂဏန်းနှိုင်းယှဉ်ချက်ကို ဖန်တီးပါ။

မကြာခဏ၊ သင်သည် ဒေတာအတွဲတစ်ခုစီတွင် တန်ဖိုးများခွဲဝေပုံကွဲပြားပုံကို နားလည်ရန် Excel ရှိ ဒေတာအတွဲနှစ်ခု၏ ကိန်းဂဏန်းအချက်အလက်များ နှိုင်းယှဉ်မှုကို လုပ်ဆောင်လိုပေမည်။

ကိန်းဂဏန်း နှိုင်းယှဉ်မှုကို လုပ်ဆောင်ရန် ဘုံနည်းလမ်း နှစ်ခုရှိသည်။

နည်းလမ်း 1- ဒေတာအတွဲတစ်ခုစီ၏ ဂဏန်းငါးလုံးအကျဉ်းချုပ်ကို တွက်ချက်ပါ။

အောက်ပါတန်ဖိုးများပါ၀င်သည့် ဒေတာအတွဲတစ်ခုစီ၏ ဂဏန်းငါးလုံးအကျဉ်းချုပ်ကို ကျွန်ုပ်တို့ တွက်ချက်နိုင်သည်-

• အနိမ့်ဆုံးတန်ဖိုး
• ပထမ quartile (25th ရာခိုင်နှုန်း)
• ပျမ်းမျှ (၅၀ ရာခိုင်နှုန်း)
• တတိယ quartile (75th percentile)
• အများဆုံး

ဤတန်ဖိုးငါးခုကို တွက်ချက်ခြင်းဖြင့် ဒေတာအစုတစ်ခုစီတွင် တန်ဖိုးများခွဲဝေမှုကို ကောင်းစွာနားလည်နိုင်မည်ဖြစ်သည်။

နည်းလမ်း 2- ပျမ်းမျှနှင့် စံသွေဖည်မှုကို တွက်ချက်ပါ။

ဒေတာအတွဲနှစ်ခု၏ ကိန်းဂဏန်းဆိုင်ရာ နှိုင်းယှဉ်မှုကို လုပ်ဆောင်ရန် ရိုးရှင်းသောနည်းလမ်းမှာ ဒေတာအတွဲတစ်ခုစီ၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို တွက်ချက်ရန်ဖြစ်သည်။

၎င်းသည် “ ဗဟို” တန်ဖိုးသည် မည်သည့်နေရာတွင်ရှိပြီး ဒေတာအစုတစ်ခုစီတွင် တန်ဖိုးများခွဲဝေမှုမှာ အဘယ်အရာဖြစ်သည်ကို အနီးစပ်ဆုံးနားလည်ရန် ကူညီပေးသည်။

အောက်ဖော်ပြပါ ဥပမာသည် ဤနည်းလမ်းတစ်ခုစီကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

ဥပမာ- Excel တွင် ဒေတာအတွဲနှစ်ခု၏ ကိန်းဂဏန်း နှိုင်းယှဉ်မှုကို လုပ်ဆောင်ပါ။

စာမေးပွဲတစ်ခုတွင်ရရှိသော မတူညီသောအတန်းနှစ်ခုမှ ကျောင်းသားများ၏ ရလဒ်များကိုပြသသော Excel တွင် ကျွန်ုပ်တို့တွင် ဒေတာနှစ်စုံရှိသည်ဆိုပါစို့။

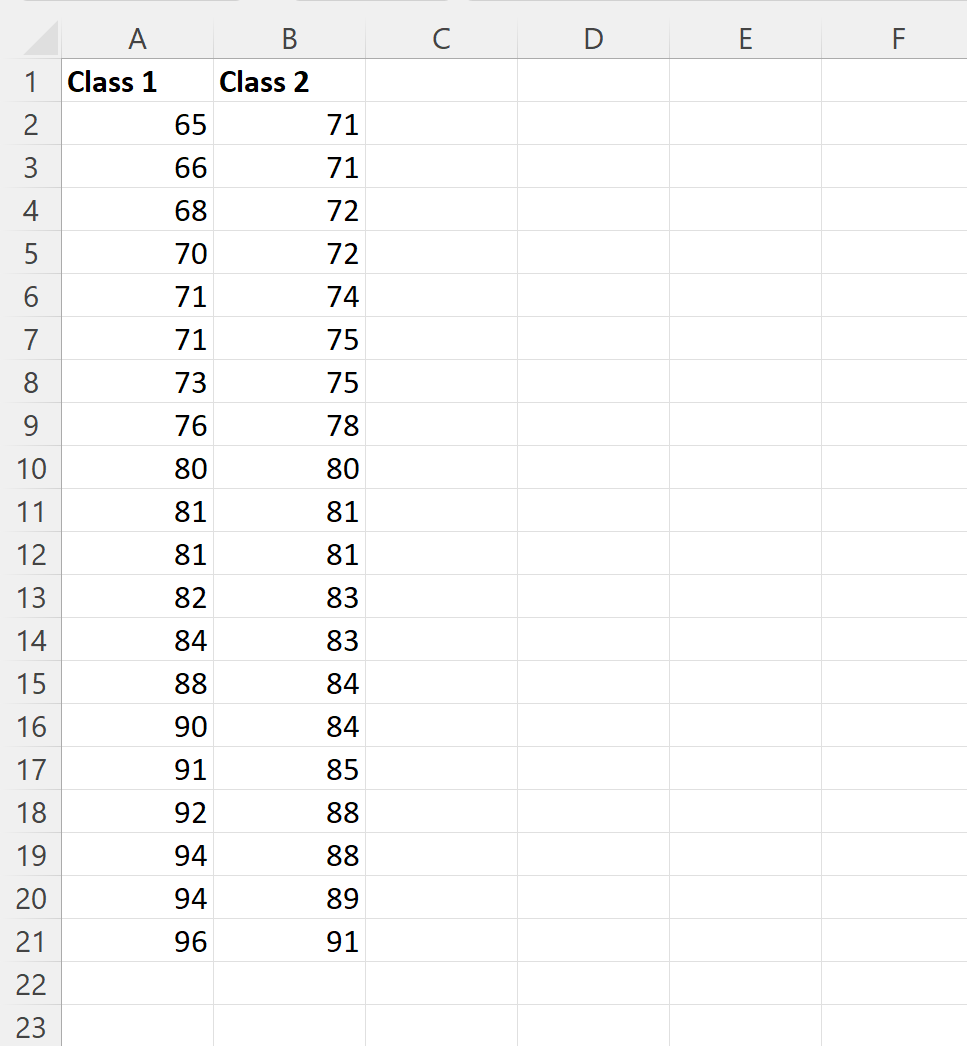
အတန်း 1 အတွက် စာမေးပွဲရလဒ်များ၏ ဂဏန်းငါးလုံးအကျဉ်းချုပ်ကို တွက်ချက်ရန် ကော်လံ E ၏ဆဲလ်များတွင် အောက်ပါဖော်မြူလာများကို ရိုက်ထည့်နိုင်သည်-

• E2 : =MIN(A2:A21)
• E3 : =QUARTILE(A2:A21၊ 1)
• E4 : =Median(A2:A21)
• E5 : =QUARTILE(A2:A21၊ 3)
• E6 : =MAX(A2:A21

ထို့နောက် အတန်း 2 အတွက် တူညီသောတန်ဖိုးများကို တွက်ချက်ရန် ဤဖော်မြူလာများကို ညာဘက်သို့ နှိပ်ပြီး ဆွဲယူနိုင်သည်-

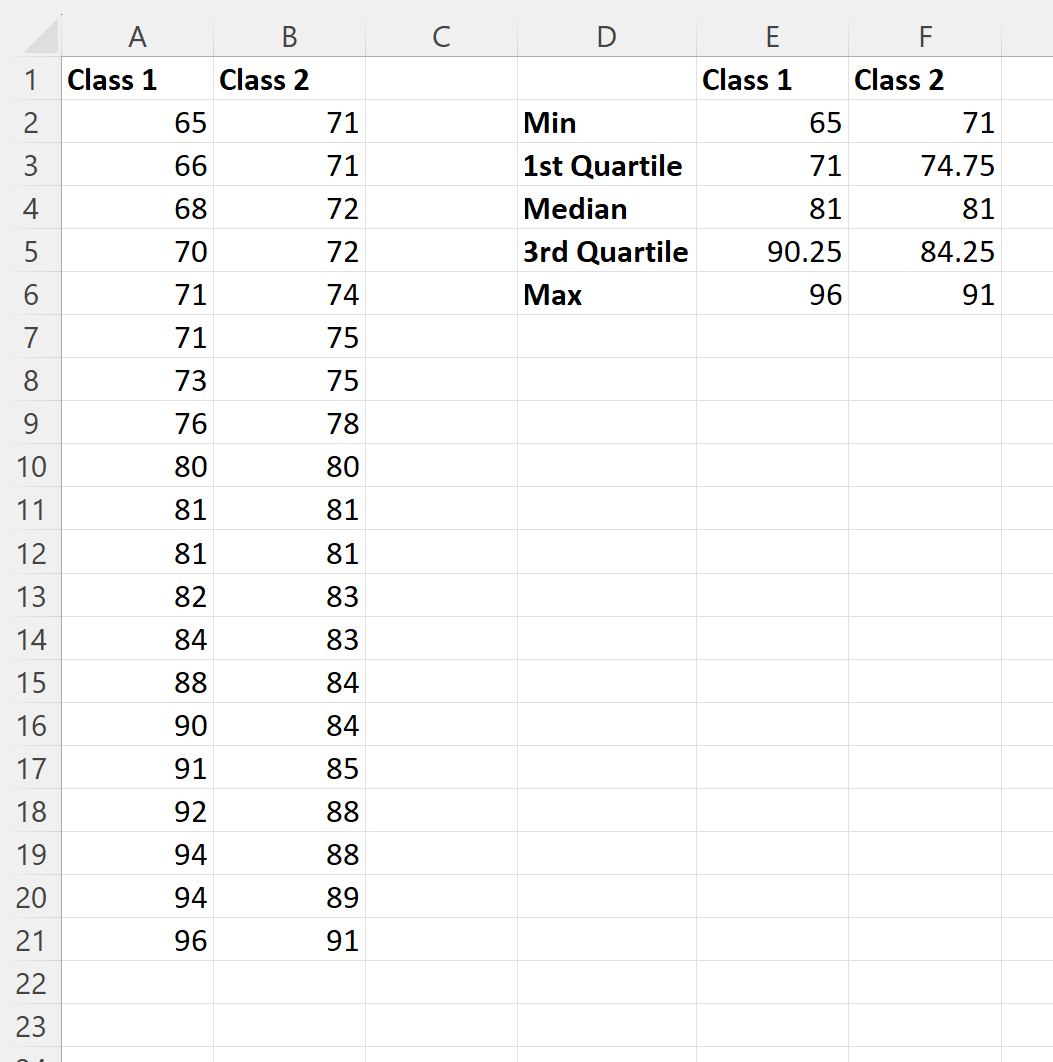
ထို့နောက် Class 1 အတွက် စာမေးပွဲရလဒ်များ၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို တွက်ချက်ရန် အောက်ပါ ဖော်မြူလာများကို ကော်လံ E ၏ဆဲလ်များအတွင်းသို့ ထည့်နိုင်သည်-

• E8 : =AVERAGE(A2:A21)
• E9 : =ETDEV(A2:A21၊ 1)

ထို့နောက် အတန်း 2 အတွက် တူညီသောတန်ဖိုးများကို တွက်ချက်ရန် ဤဖော်မြူလာများကို ညာဘက်သို့ နှိပ်ပြီး ဆွဲယူနိုင်သည်-

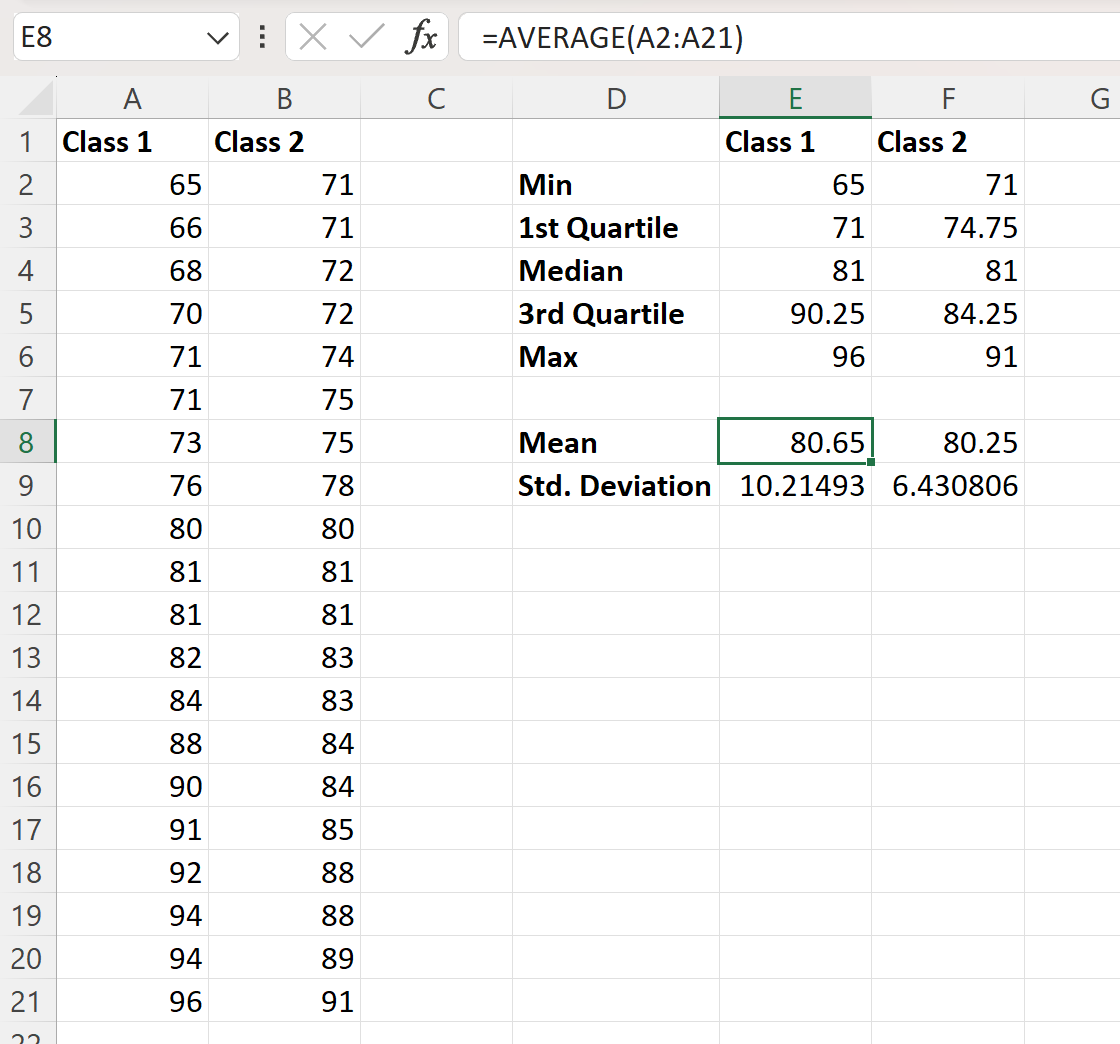
ဒေတာအတွဲနှစ်ခု၏ ဤစာရင်းအင်းနှိုင်းယှဉ်မှုမှ အောက်ပါကောက်ချက်များအား ကျွန်ုပ်တို့ ထုတ်ယူနိုင်သည်-

နိဂုံး 1- ဒေတာအတွဲနှစ်ခုလုံးသည် အလားတူ “core” တန်ဖိုးရှိသည်။

ဒေတာအတွဲနှစ်ခုစလုံးတွင် ပျမ်းမျှစာမေးပွဲရမှတ် 81 ရှိသည်။ ပျမ်းမျှတန်ဖိုးများသည် အနည်းငယ်သာကွာခြားသည်- ပထမတန်းတွင် ပျမ်းမျှစာမေးပွဲရမှတ် 80.65 ရှိပြီး ဒုတိယတန်းတွင် ပျမ်းမျှစာမေးပွဲရမှတ် 80.65 ရှိပြီး ဒုတိယတန်းတွင် ပျမ်းမျှစာမေးပွဲရမှတ် 80.65 ရှိသည်။ 80.65′ သုံးသပ်ချက် 80.25။

၎င်းသည် အတန်းနှစ်ခုကြားရှိ “ core” သို့မဟုတ် “ ပုံမှန်” စာမေးပွဲရမှတ်သည် တူညီကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

နိဂုံး 2- ပထမဒေတာအတွဲတွင် တန်ဖိုးများ ပိုမိုကြီးမားသော “ကွဲလွဲမှု” ရှိသည်။

ပထမတန်းစာမေးပွဲများ၏ ရလဒ်များသည် ဒုတိယတန်းစာမေးပွဲများထက် များစွာပို၍ကွဲပြားကြောင်း ညွှန်ကိန်းအများအပြားက ကျွန်ုပ်တို့ကို ပြောပြသည်။

ဥပမာအားဖြင့်၊ class 1 ၏ scope သည် အလွန်မြင့်မားသည်-

• အတန်းအစား 1 အပိုင်း- 96 – 65 = 31
• အတန်းအစား 2 အပိုင်း- 91 – 71 = 20

class 1 ၏ interquartile range သည် အလွန်မြင့်မားသည်-

• အတန်းအစား 1 ကြားကြားအကွာအဝေး- 90.25 – 71 = 19.25
• အတန်းအစား 2 ကြားကြားအကွာအဝေး- 84.25 မှ 74.75 = 9.5

အတန်း 1 ၏ စံသွေဖည်မှုမှာလည်း ပိုမိုမြင့်မားသည်-

• အတန်းအစား 1 စံသွေဖည်- 10.21
• အတန်းအစား 2: 6.43 ၏ စံသွေဖည်မှု

ဤအစီအမံတစ်ခုစီတိုင်းသည် Class 1 ကျောင်းသားများအတွက် စာမေးပွဲရမှတ်ကွာဟချက်သည် Class 2 အတွက်ထက် များစွာမြင့်မားကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် အခြားသော အသုံးများသည့် လုပ်ဆောင်ချက်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင် Summary Table ဖန်တီးနည်း
Excel တွင် အုပ်စုအလိုက် ပျမ်းမျှတွက်နည်း
Excel တွင် Standard Deviation နှင့် Zero ကို လျစ်လျူရှုနည်း