Excel တွင် regression ၏ standard error တွက်ချက်နည်း
ကျွန်ုပ်တို့သည် linear regression model နှင့် ကိုက်ညီသည်၊ မော်ဒယ်သည် အောက်ပါပုံစံအတိုင်းဖြစ်သည်-
Y = β 0 + β 1 X + … + β i
ϵ သည် X နှင့် ကင်းသော အမှားအယွင်းတစ်ခုဖြစ်သည်။
Y ၏တန်ဖိုးများကိုခန့်မှန်းရန် X ကိုမည်မျှအသုံးပြုနိုင်ပါစေ၊ မော်ဒယ်တွင်ကျပန်းအမှားအမြဲရှိလိမ့်မည်။
ဤကျပန်းအမှား၏ပြန့်ပွားမှုကိုတိုင်းတာရန်နည်းလမ်းတစ်ခုမှာ ကျန်ရှိသောအကြွင်း အကျန်များ၏စံသွေဖည်မှုကိုတိုင်းတာသည့်နည်းလမ်းဖြစ် သည့် regression model ၏စံအမှားကို အသုံးပြုခြင်းဖြစ်သည်။
ဤသင်ခန်းစာသည် Excel ရှိ regression model တစ်ခု၏ စံအမှားကို တွက်ချက်နည်း အဆင့်ဆင့် ဥပမာကို ပေးပါသည်။
အဆင့် 1: ဒေတာကိုဖန်တီးပါ။
ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် မတူညီသောကျောင်းသား 12 ဦးအတွက် အောက်ပါ variable များပါရှိသော ဒေတာအတွဲတစ်ခုကို ဖန်တီးပါမည်။
- စာမေးပွဲရလဒ်
- နာရီပေါင်းများစွာ စာသင်ခဲ့ရသည်။
- လက်ရှိအတန်း
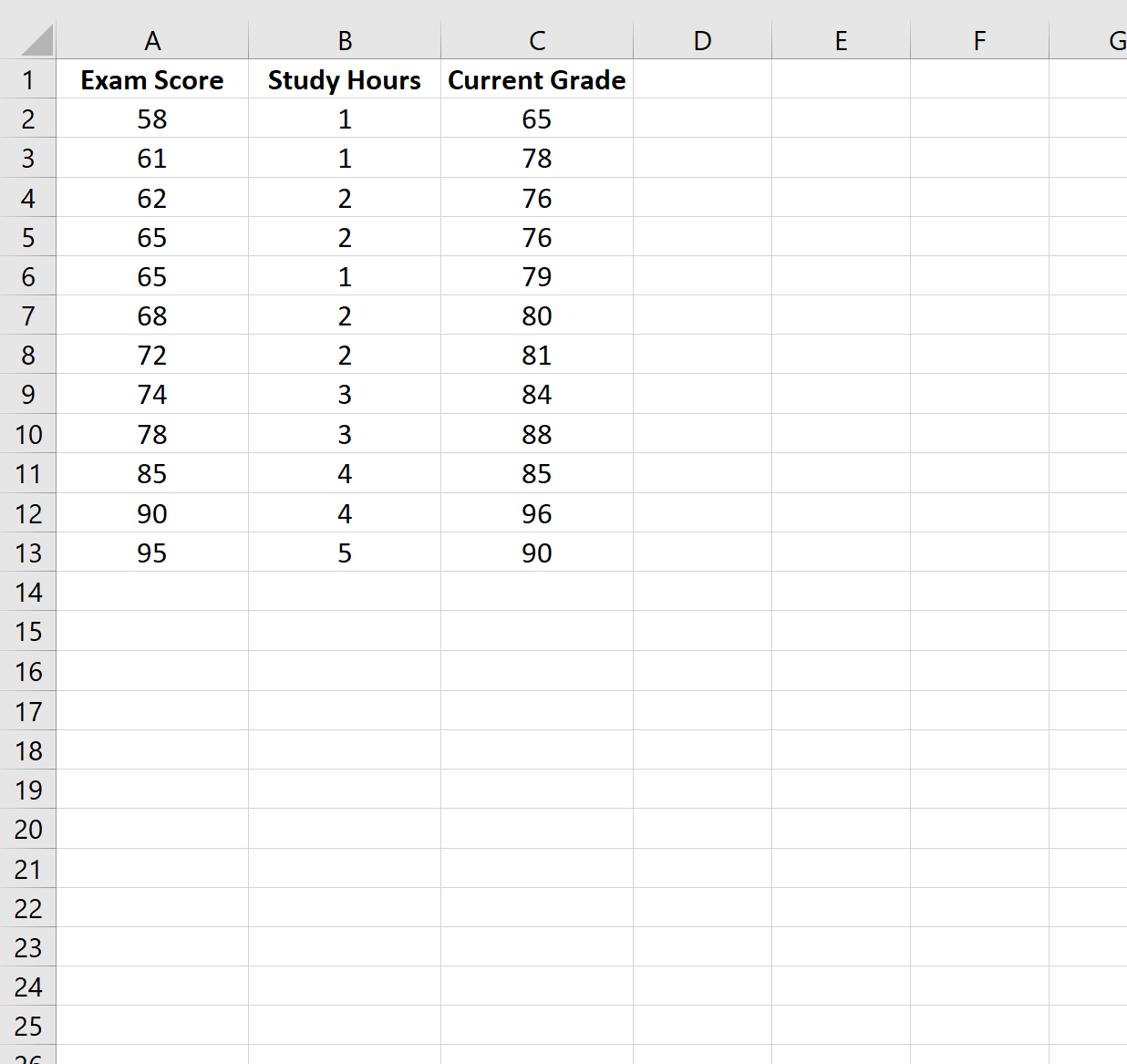
အဆင့် 2- ဆုတ်ယုတ်မှုပုံစံကို အံကိုက်လုပ်ပါ။
ထို့နောက်၊ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုကိန်းရှင် နှင့် စာသင်ချိန် နှင့် လက်ရှိအဆင့်ကို ကြိုတင်ခန့်မှန်းကိန်းရှင်များအဖြစ် စာမေးပွဲရမှတ်ကို အသုံးပြု၍ များစွာသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု ပုံစံကို ဖြည့်သွင်းပါမည်။
၎င်းကိုလုပ်ဆောင်ရန် ထိပ်ဖဲကြိုးတစ်လျှောက်ရှိ Data tab ကိုနှိပ်ပါ၊ ထို့နောက် Data Analysis ကို နှိပ်ပါ။

ဤရွေးချယ်ခွင့်ကို မရရှိနိုင်ပါက၊ Data Analysis ToolPak ကို ဦးစွာ စတင်ရပါ မည်။
ပေါ်လာသောဝင်းဒိုးတွင်၊ Regression ကို ရွေးချယ်ပါ။ ပေါ်လာသည့်ဝင်းဒိုးအသစ်တွင်၊ အောက်ပါအချက်အလက်များကို ပေးဆောင်ပါ-
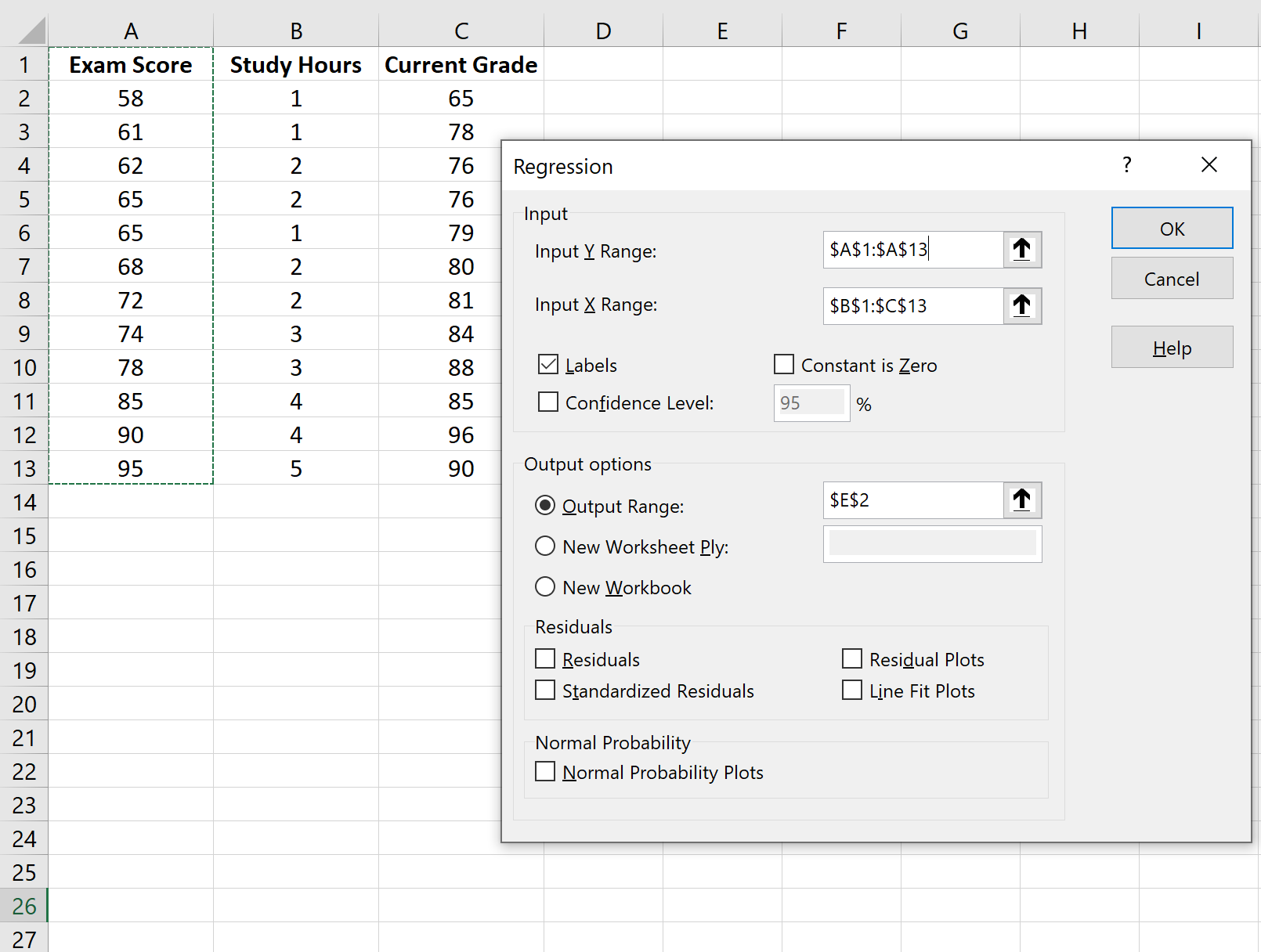
OK ကိုနှိပ်လိုက်သည်နှင့် regression model output ပေါ်လာပါမည်။
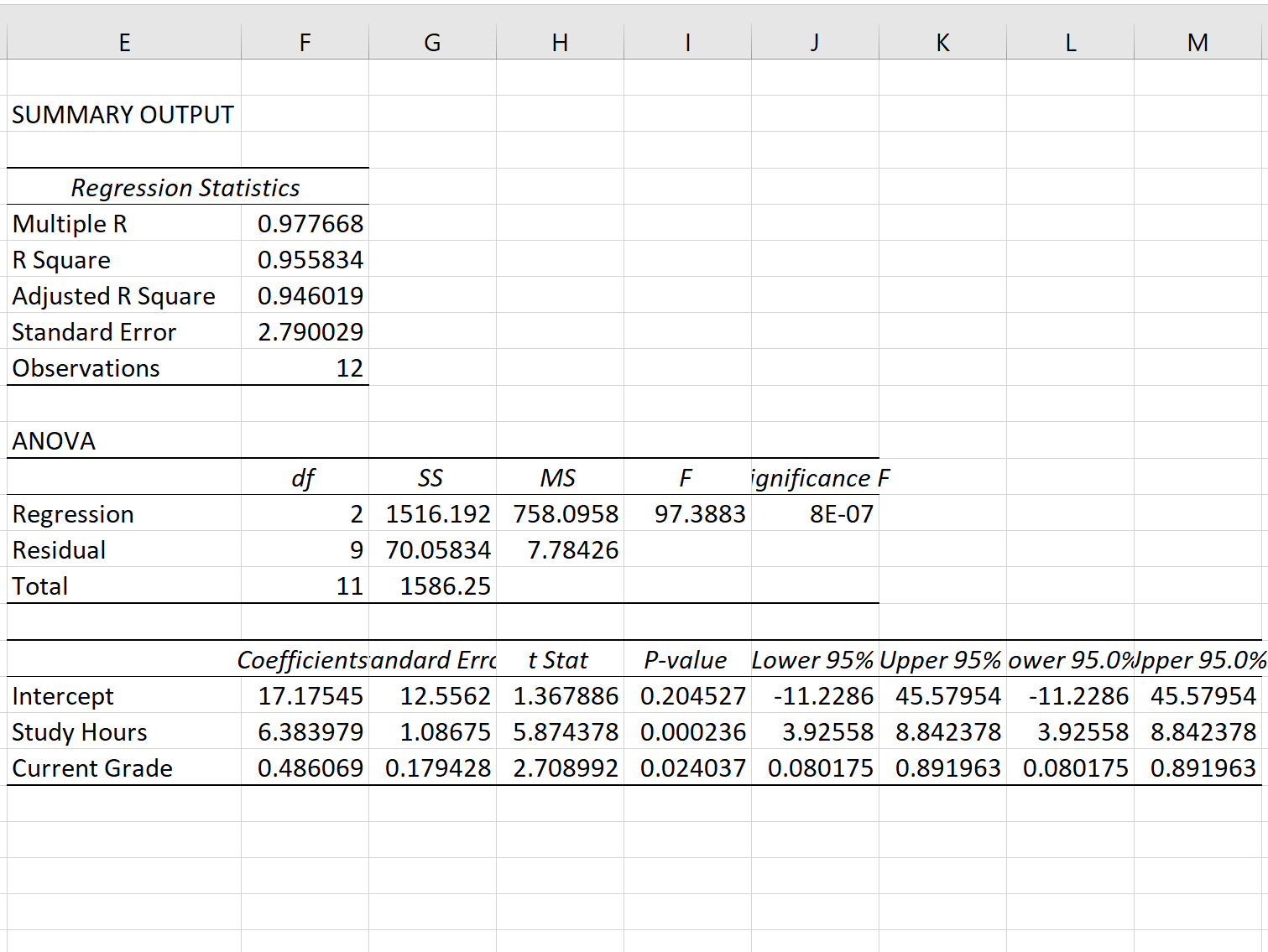
အဆင့် 3- ဆုတ်ယုတ်မှုစံအမှားကို အဓိပါယ်ဖွင့်ဆိုပါ။
ဆုတ်ယုတ်မှုပုံစံ၏ စံအမှားသည် စံအမှား ဘေးရှိ နံပါတ်ဖြစ်သည်
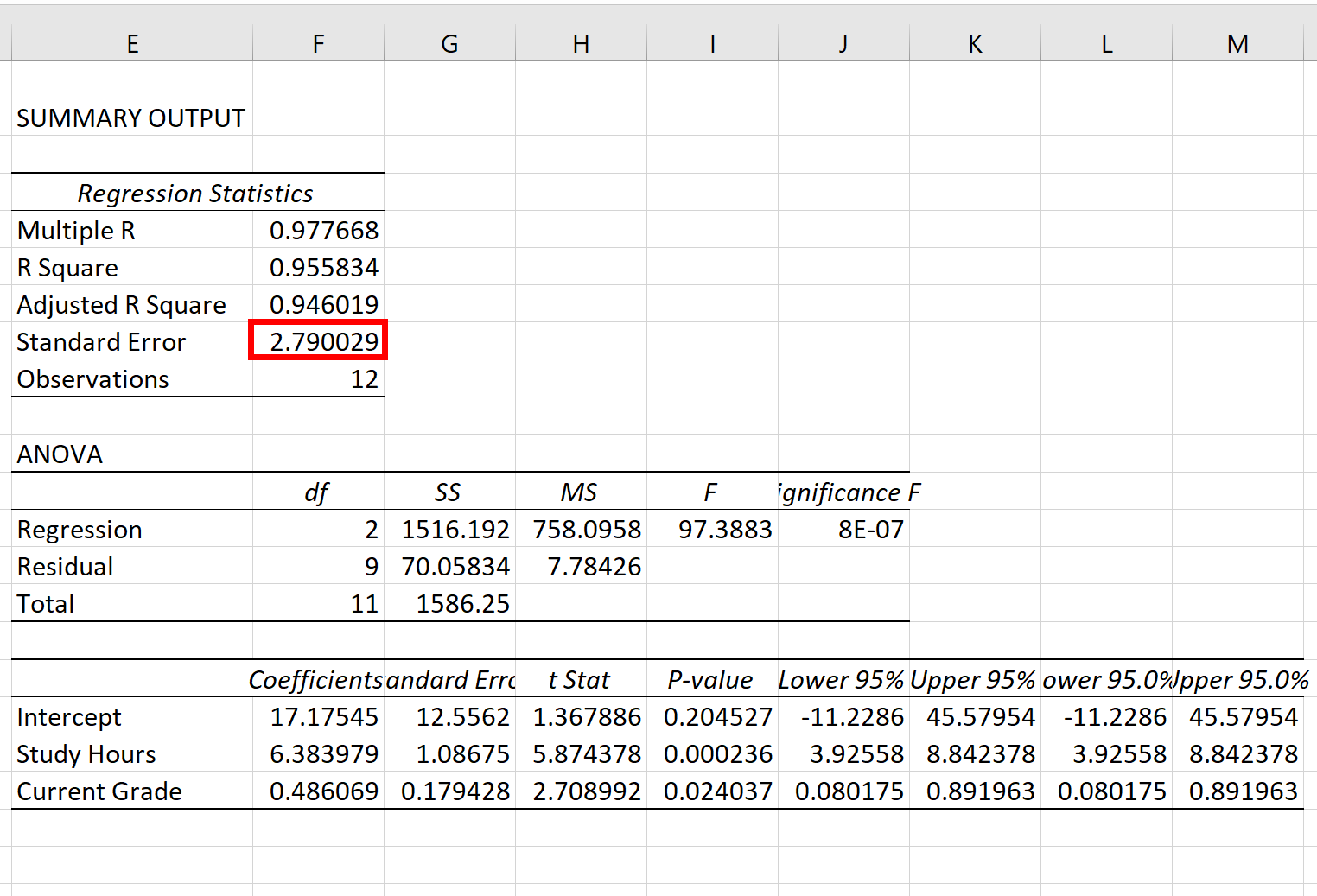
ဤအထူးဆုတ်ယုတ်မှုပုံစံ၏ စံအမှားသည် 2.790029 ဖြစ်သွားသည်။
ဤနံပါတ်သည် အမှန်တကယ် စာမေးပွဲရလဒ်များနှင့် မော်ဒယ်မှ ခန့်မှန်းထားသော စာမေးပွဲရလဒ်များကြား ပျမ်းမျှအကွာအဝေးကို ကိုယ်စားပြုသည်။
အချို့သော စာမေးပွဲရလဒ်များသည် ခန့်မှန်းရမှတ်ထက် 2.79 ယူနစ်ထက် ပိုဝေးနေမည်ဖြစ်ပြီး အချို့မှာ ပိုနီးစပ်မည်ဟု သတိပြုပါ။ သို့သော် ပျမ်းမျှအားဖြင့်၊ အမှန်တကယ် စာမေးပွဲရလဒ်များနှင့် ခန့်မှန်းရလဒ်များကြား အကွာအဝေးမှာ 2.790029 ဖြစ်သည်။
ဆုတ်ယုတ်မှု၏ သေးငယ်သော စံအမှားတစ်ခုသည် ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာအတွဲတစ်ခုနှင့် ပိုမိုနီးကပ်စွာကိုက်ညီကြောင်း သတိပြုပါ။
ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဒေတာသတ်မှတ်မှုတွင် ဆုတ်ယုတ်မှုပုံစံအသစ်ကို ဖြည့်သွင်းပြီး 4.53 ၏ စံအမှားတစ်ခုကို ရယူပါက၊ ဤပုံစံသစ်သည် ယခင်မော်ဒယ်ထက် စာမေးပွဲရမှတ်များကို ခန့်မှန်းရာတွင် ထိရောက်မှုနည်းမည်ဖြစ်သည်။
ထပ်လောင်းအရင်းအမြစ်များ
ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ တိကျမှုကို တိုင်းတာရန် နောက်ထပ်ဘုံနည်းလမ်းမှာ R-squared ကို အသုံးပြုခြင်းဖြစ်သည်။ တိကျမှုနှင့် R-squared ကိုတိုင်းတာရန် ဆုတ်ယုတ်မှု၏စံအမှားကို အသုံးပြုခြင်း၏ အကျိုးကျေးဇူးများကို ဤဆောင်းပါးတွင် ဖတ်ရှုကြည့်ပါ။