Excel တွင် z ရမှတ်မှ p တန်ဖိုးကို မည်သို့ရှာမည်နည်း။
ကိန်းဂဏန်းများဆိုင်ရာ ယူဆချက်စစ်ဆေးမှုများ စွာသည် z-test ကိန်းဂဏန်းကို ဖြစ်ပေါ်စေသည်။ ဤ z-test ကိန်းဂဏန်းကို ရှာတွေ့သည်နှင့် ၎င်းနှင့် ဆက်စပ်နေသည့် p-value ကို တွေ့ရတတ်သည်။ ဤ p-value သည် အချို့သော alpha အဆင့် (ဥပမာ 0.10၊ 0.05၊ 0.01) အောက်တွင် ရှိနေပါက၊ ကျွန်ုပ်တို့သည် စမ်းသပ်မှု၏ null hypothesis ကို ငြင်းပယ်ပြီး ကျွန်ုပ်တို့၏ ရလဒ်များသည် သိသာထင်ရှားသည်ဟု ကောက်ချက်ချပါသည်။
ဤသင်ခန်းစာသည် NORM.DIST လုပ်ဆောင်ချက်ကို အသုံးပြု၍ Excel ရှိ z-score မှ p-value ကိုရှာဖွေခြင်း၏နမူနာများစွာကို သရုပ်ပြထားပြီး၊
NORM.DIST (x၊ ပျမ်းမျှ၊ standard_dev၊ စုစည်းမှု)
ရွှေ-
- x သည် ကျွန်ုပ်တို့စိတ်ဝင်စားသော z ရမှတ်ဖြစ်သည်။
- mean သည် ဖြန့်ဖြူးမှု၏ ဆိုလိုရင်းဖြစ်သည်၊ ကျွန်ုပ်တို့သည် စံပုံမှန်ဖြန့်ဝေမှုအတွက် “ 0” ကို အသုံးပြုပါမည်။
- standard_dev သည် ဖြန့်ဖြူးမှု၏ စံသွေဖည်မှုဖြစ်သည် – ကျွန်ုပ်တို့သည် စံပုံမှန်ဖြန့်ဝေမှုအတွက် “1” ကို အသုံးပြုပါမည်။
- စုစည်းမှု တန်ဖိုးသည် “TRUE” (CDF ကိုပြန်ပေးသည်) သို့မဟုတ် “FALSE” (PDF ကိုပြန်ပေးသည်) – စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်၏တန်ဖိုးကိုရရှိရန် “TRUE” ကိုအသုံးပြုပါမည်။
ဥပမာအချို့ကိုကြည့်ကြပါစို့။
ဥပမာ 1- Z ရမှတ်မှ P တန်ဖိုးကို ရှာဖွေခြင်း (အမြီးနှစ်ကြောင်း စမ်းသပ်မှု)
ကုမ္ပဏီတစ်ခုသည် ဘက်ထရီ အမျိုးအစားအသစ်တွင် ပျမ်းမျှသက်တမ်း 18 နာရီရှိသည့် လက်ရှိပုံမှန် ဘက်ထရီထက် ပျမ်းမျှသက်တမ်း ကွာခြားမှုရှိမရှိ သိလိုပါသည်။ ဘက်ထရီအသစ် 100 ၏ ကျပန်းနမူနာတစ်ခုတွင် ပျမ်းမျှသက်တမ်းသည် 19 နာရီဖြစ်ပြီး စံသွေဖည်မှု 4 နာရီဖြစ်ကြောင်း တွေ့ရှိရသည်။
ဘက်ထရီအသစ်၏ ပျမ်းမျှသက်တမ်းသည် လက်ရှိပုံမှန် ဘက်ထရီ၏ ပျမ်းမျှသက်တမ်းနှင့် ကွာခြားမှုရှိမရှိ ဆုံးဖြတ်ရန် အယ်လ်ဖာအဆင့် 0.05 ကို အသုံးပြု၍ အမြီးနှစ်ကြောင်း သီအိုရီစမ်းသပ်မှုကို ပြုလုပ်ပါ။
အဆင့် 1- အယူအဆများကို ဖော်ပြပါ။
null hypothesis (H 0 ): μ = 18
အစားထိုးယူဆချက်- (Ha): μ ≠ ၁၈
အဆင့် 2- z-test ကိန်းဂဏန်းကို ရှာပါ။
စမ်းသပ်စာရင်းအင်း z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2.5
အဆင့် 3- Excel ကို အသုံးပြု၍ z-test ကိန်းဂဏန်း၏ p-တန်ဖိုးကို ရှာပါ။
z = 2.5 အတွက် p-value ကိုရှာရန်၊ Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုပါမည်- =1 – NORM.DIST(2.5၊ 0၊ 1၊ TRUE)
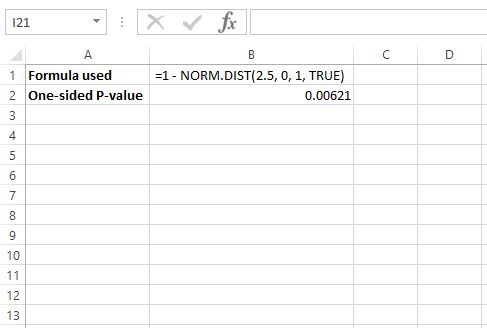
တစ်ဖက်သတ် p-value သည် .00621 ဖြစ်သည်၊ သို့သော် ကျွန်ုပ်တို့သည် အမြီးနှစ်ပိုင်းစမ်းသပ်မှုကို လုပ်ဆောင်နေသောကြောင့် ဤတန်ဖိုးကို 2 နှင့် မြှောက်ရန် လိုအပ်သောကြောင့် p-value သည် .00612 * 2 = .01224 ဖြစ်လိမ့်မည်။
အဆင့် 4- null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် ငြင်းပယ်ခြင်းမပြုပါနှင့်။
0.01224 ၏ p-value သည် ရွေးချယ်ထားသော alpha အဆင့် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။ ဘက်ထရီအသစ်၏ ပျမ်းမျှသက်တမ်းသည် လက်ရှိပုံမှန် ဘက်ထရီ၏ ပျမ်းမျှသက်တမ်းနှင့် သိသိသာသာကွာခြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားများရှိသည်။
ဥပမာ 2- Z ရမှတ်မှ P တန်ဖိုးကို ရှာဖွေခြင်း (တစ်ဖက်သတ်စမ်းသပ်မှု)
အပင်တစ်ပင်၏ ပျမ်းမျှအမြင့်သည် ၁၄ လက်မထက်နည်းသည်ဟု ရုက္ခဗေဒပညာရှင်တစ်ဦးက ခန့်မှန်းသည်။ သူမသည် အပင် 30 ကို ကျပန်းရွေးချယ်ပြီး တိုင်းတာသည်။ ပျမ်းမျှအရပ်သည် 13.5 လက်မဖြစ်ပြီး စံသွေဖည်မှု 2 လက်မရှိကြောင်း သူမတွေ့ရှိခဲ့သည်။
ဤအပင်၏ပျမ်းမျှအမြင့်သည် အမှန်တကယ် 14 လက်မအောက်ရှိမရှိဆုံးဖြတ်ရန် alpha အဆင့် 0.01 ကိုအသုံးပြု၍ တစ်ဖက်သတ်ယူဆချက်စမ်းသပ်မှုပြုလုပ်ပါ။
အဆင့် 1- အယူအဆများကို ဖော်ပြပါ။
null hypothesis (H0): μ≥ 14
အခြားယူဆချက်- (Ha): μ < ၁၄
အဆင့် 2- z-test ကိန်းဂဏန်းကို ရှာပါ။
စမ်းသပ်စာရင်းအင်း z = (x-μ) / (s/√n) = (13.5-14) / (2/√30) = -1.369
အဆင့် 3- Excel ကို အသုံးပြု၍ z-test ကိန်းဂဏန်း၏ p-တန်ဖိုးကို ရှာပါ။
z = -1.369 အတွက် p-value ကိုရှာရန်၊ Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုပါမည်- =NORM.DIST(-1.369, 0, 1, TRUE)
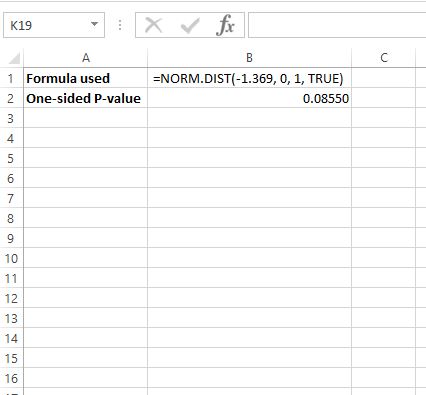
၎င်းသည် တစ်ဖက်သတ် p-value သည် 0.08550 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ကို ပြောပြသည်။
အဆင့် 4- null hypothesis ကို ငြင်းပယ်ခြင်း သို့မဟုတ် ငြင်းပယ်ခြင်းမပြုပါနှင့်။
0.08550 ၏ p-value သည် ရွေးချယ်ထားသော alpha အဆင့် 0.01 ထက် ကြီးသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ဤအပင်မျိုးစိတ်များ၏ ပျမ်းမျှအမြင့်သည် ၁၄ လက်မထက်နည်းသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားမရှိပါ။
Excel ရှိ စာရင်းအင်းဆိုင်ရာ သင်ခန်းစာများအတွက် နောက်ထပ်သင်ခန်းစာများအတွက်၊ ကျွန်ုပ်တို့၏ Excel လမ်းညွှန်များ စာရင်းအပြည့်အစုံကို စစ်ဆေးကြည့်ပါ ။