Excel- linear regression များစွာကိုလုပ်ဆောင်ရန် linest ကိုအသုံးပြုနည်း

များစွာသော linear regression model ကို data အစုတစ်ခုနှင့် ကိုက်ညီရန် Excel တွင် LINEST လုပ်ဆောင်ချက်ကို သင်အသုံးပြုနိုင်ပါသည်။

ဤလုပ်ဆောင်ချက်သည် အောက်ပါအခြေခံ syntax ကိုအသုံးပြုသည်-

 = LINEST ( known_y's, [known_x's], [const], [stats] )

ရွှေ-

• Know_y’s : သိထားသော y တန်ဖိုးများ array တစ်ခု
• Know_x’s : သိထားသော x တန်ဖိုးများ array တစ်ခု
• const : ရွေးချယ်နိုင်သော အကြောင်းပြချက်။ မှန်ပါက၊ ကိန်းသေ b ကို ပုံမှန်အတိုင်း လုပ်ဆောင်သည်။ မှားပါက၊ ကိန်းသေ b ကို 1 ဟု သတ်မှတ်သည်။
• ကိန်းဂဏာန်းများ – ရွေးချယ်နိုင်သော အကြောင်းပြချက်။ မှန်ပါက၊ ထပ်ဆင့်ဆုတ်ယုတ်မှုစာရင်းအင်းများကို ပြန်ပေးသည်။ မှားပါက၊ နောက်ထပ် ဆုတ်ယုတ်မှုစာရင်းအင်းများကို ပြန်ပေးမည်မဟုတ်ပါ။

အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့တွင် မည်သို့အသုံးပြုရမည်ကို ပြသထားသည်။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

ပထမဦးစွာ၊ Excel တွင်အောက်ပါဒေတာအစုံထည့်ကြပါစို့။

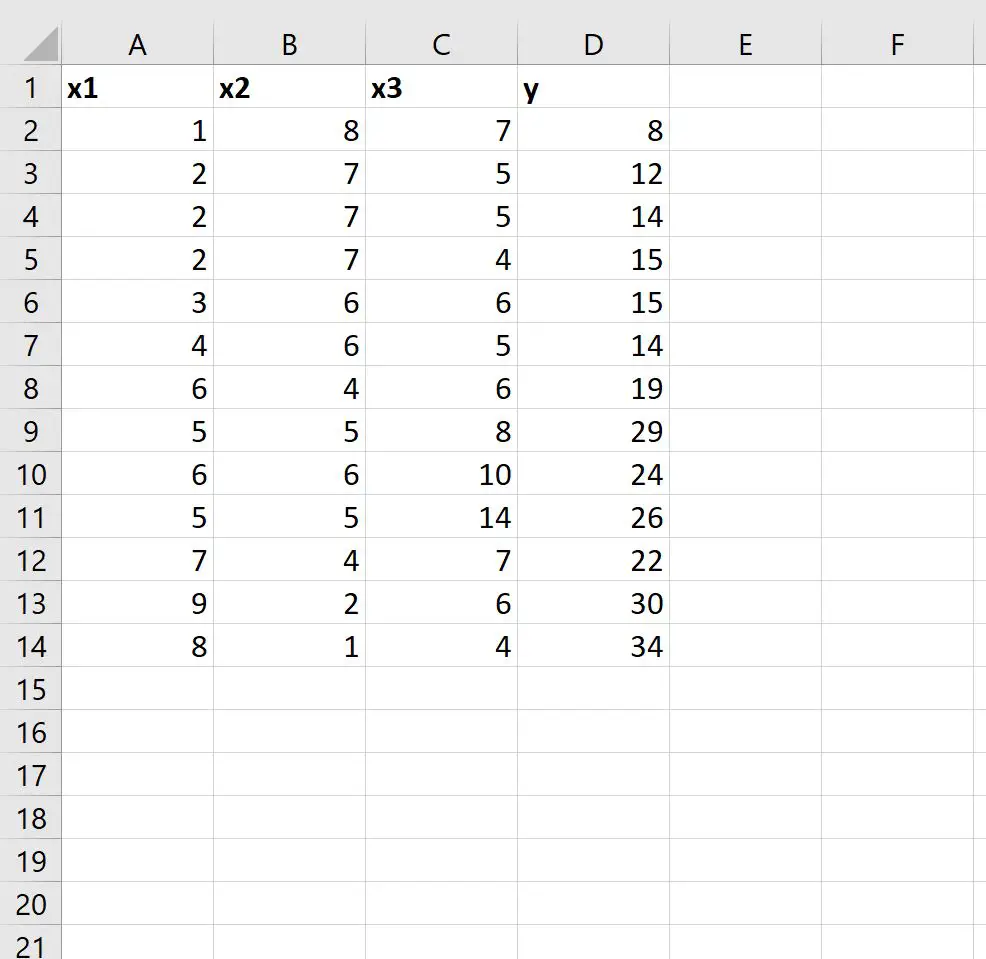
အဆင့် 2- မျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံမျိုးစုံကို အံဝင်ခွင်ကျဖြစ်အောင် LINEST ကိုသုံးပါ။

ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် y ကို တုံ့ပြန်မှုကိန်းရှင်အဖြစ် x1 ၊ x2 နှင့် x3 ကိုအသုံးပြု၍ များစွာသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံတစ်ခုကို ကျွန်ုပ်တို့ အံဝင်ခွင်ကျဖြစ်စေလိုသည်ဆိုပါစို့။

ဒါကိုလုပ်ဖို့၊ ဒီ multiple linear regression model နဲ့ကိုက်ညီအောင် အောက်ပါဖော်မြူလာကို ဘယ်ဆဲလ်ထဲမှာမဆို ရိုက်ထည့်နိုင်ပါတယ်။

 =LINEST( D2:D14 , A2:C14 )

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဖော်မြူလာကို လက်တွေ့တွင် အသုံးပြုနည်းကို ပြသသည်-

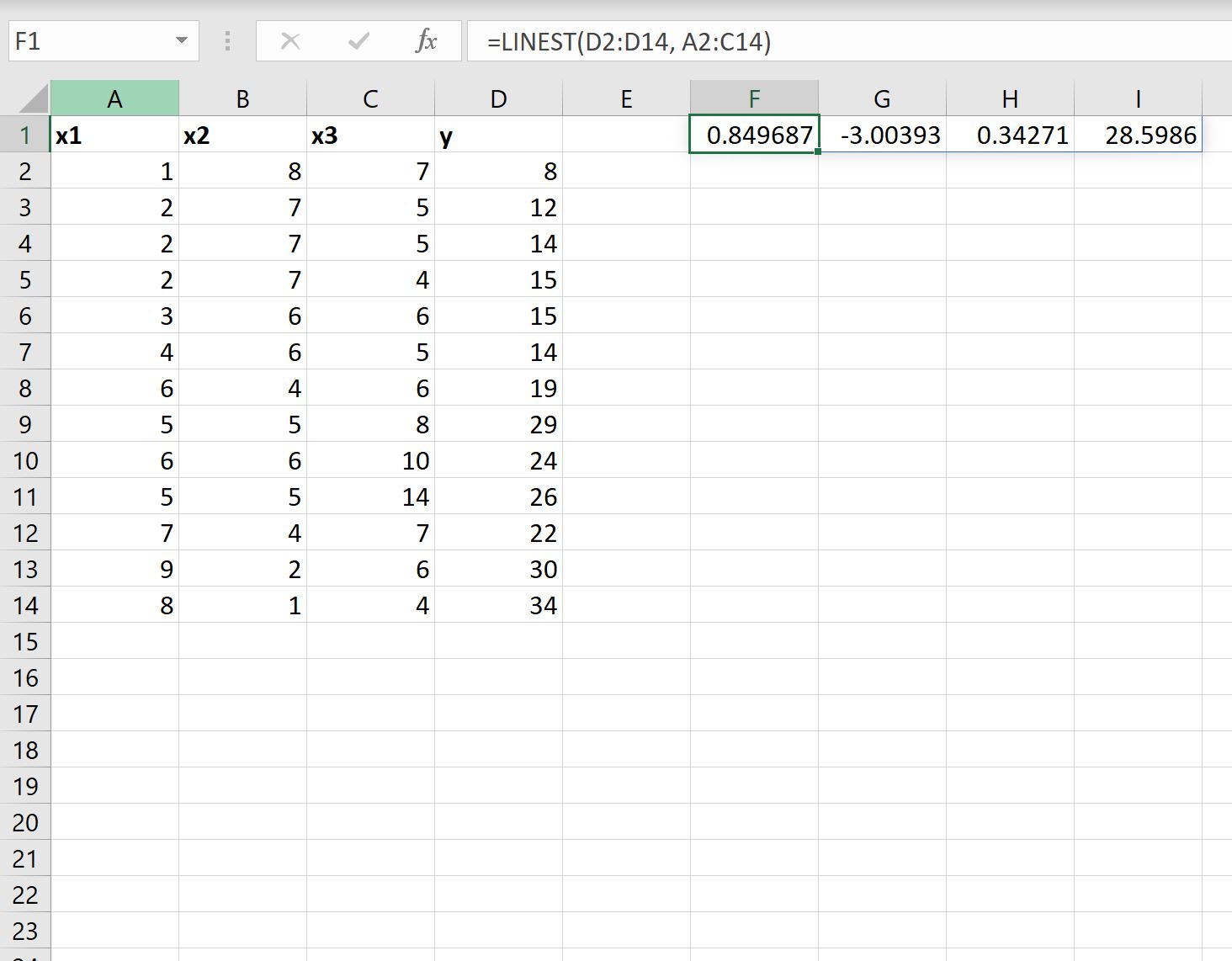
ဤသည်မှာ ရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

• ကြားဖြတ်၏ coefficient သည် 28.5986 ဖြစ်သည်။
• x1 အတွက် coefficient သည် 0.34271 ဖြစ်သည်။
• x2 အတွက် coefficient သည် -3.00393 ဖြစ်သည်။
• x3 အတွက် coefficient သည် 0.849687 ဖြစ်သည်။

ဤကိန်းဂဏန်းများကို အသုံးပြု၍ တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုညီမျှခြင်းအား အောက်ပါအတိုင်း ရေးသားနိုင်ပါသည်။

y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)

အဆင့် 3 (ချန်လှပ်ထားနိုင်သည်)- နောက်ထပ် ဆုတ်ယုတ်မှုစာရင်းအင်းများကို ကြည့်ပါ။

တပ်ဆင်ထားသော ဆုတ်ယုတ်မှု ညီမျှခြင်း အတွက် ထပ်လောင်းဆုတ်ယုတ်မှုကိန်းဂဏန်းများကိုပြသရန် LINEST လုပ်ဆောင်ချက်ရှိ ကိန်းဂဏန်း အငြင်းအခုံ၏တန်ဖိုးကိုလည်း သတ်မှတ်နိုင်သည်-

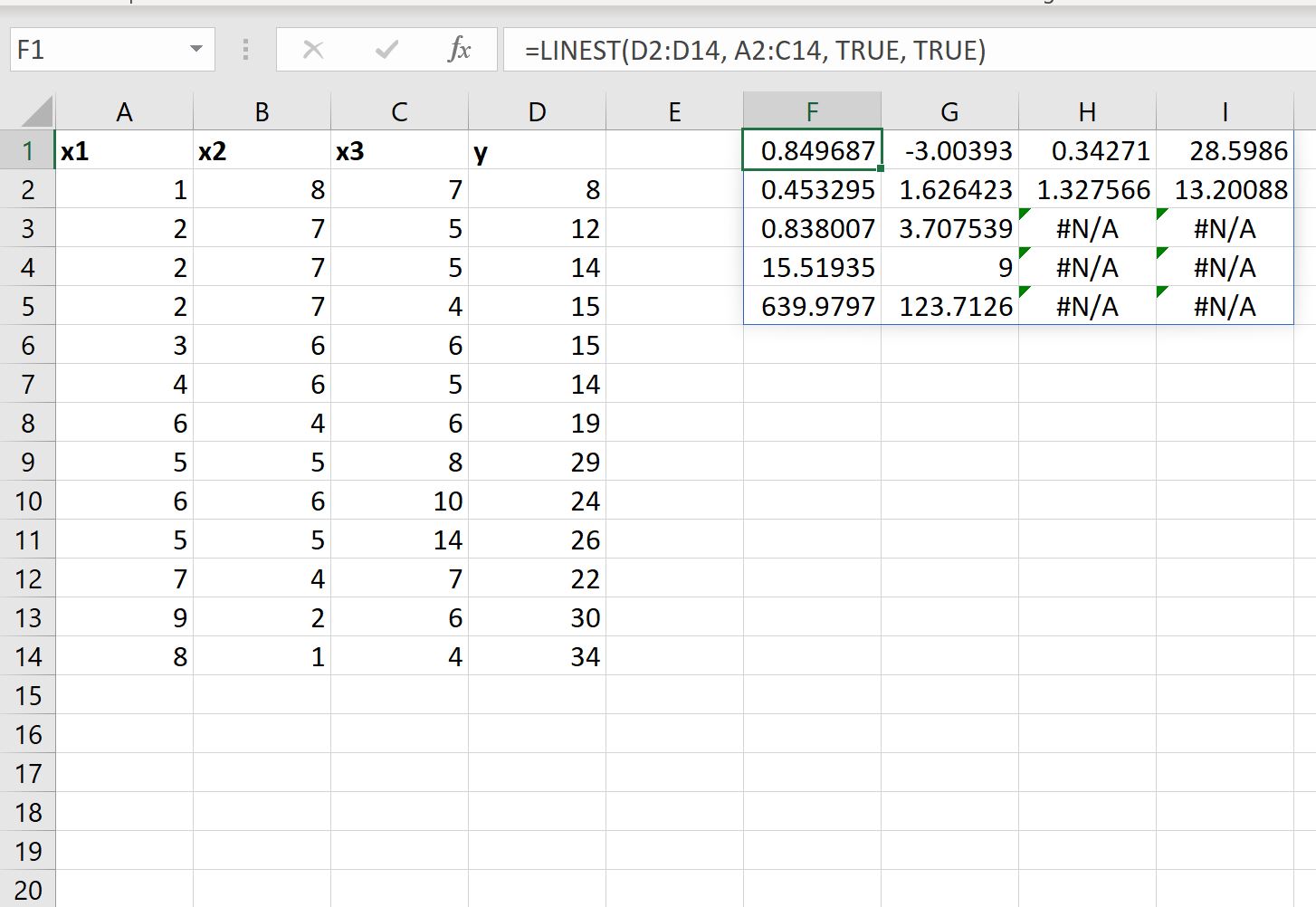
တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုညီမျှခြင်းသည် အတူတူပင်ဖြစ်သည်-

y = 28.5986 + 0.34271(x1) – 3.00393(x2) + 0.849687(x3)

ဤသည်မှာ ရလဒ်၏ အခြားတန်ဖိုးများကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည် ။

• x3 အတွက် standard error သည် 0.453295 ဖြစ်သည်။
• x2 အတွက် စံအမှားမှာ 1.626423 ဖြစ်သည်။
• x1 အတွက် စံအမှားမှာ 1.327566 ဖြစ်သည်။
• ကြားဖြတ်အတွက် စံအမှားမှာ 13.20088 ဖြစ်သည်။
• မော်ဒယ်၏ R ² သည် .838007 ဖြစ်သည်။
• y အတွက် ကျန်နေသော စံအမှားသည် 3.707539 ဖြစ်သည်။
• စုစုပေါင်း F ကိန်းဂဏန်းသည် 15.51925 ဖြစ်သည်။
• လွတ်လပ်မှု အဆင့် ၉ ။
• နှစ်ထပ်ကိန်းများ၏ ဆုတ်ယုတ်မှုပေါင်းလဒ်သည် 639.9797 ဖြစ်သည်။
• ကျန်ရှိသော စတုရန်း၏ပေါင်းလဒ်သည် 123.7126 ဖြစ်သည်။

ယေဘုယျအားဖြင့်၊ ဤနောက်ထပ်ကိန်းဂဏန်းစာရင်းဇယားများတွင် စိတ်ဝင်စားမှုအများဆုံးတိုင်းတာမှုမှာ ခန့်မှန်းသူကိန်းရှင်ဖြင့်ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်းရှင်၏ကွဲလွဲမှုအချိုးအစားကိုကိုယ်စားပြုသည့် R ² တန်ဖိုးဖြစ်သည်။

R ² ၏တန်ဖိုးသည် 0 မှ 1 အထိကွဲပြားနိုင်သည်။

ဤအထူးမော်ဒယ်၏ R ² သည် 0.838 ဖြစ်သောကြောင့်၊ ခန့်မှန်းသူကိန်းရှင်များသည် တုံ့ပြန်မှုကိန်းရှင် y ၏တန်ဖိုးကို ခန့်မှန်းရန် ကောင်းမွန်သောအလုပ်ဖြစ်ကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

ဆက်စပ်မှု- ကောင်းသော R-squared တန်ဖိုးဆိုသည်မှာ အဘယ်နည်း။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် အခြားသော ဘုံလုပ်ဆောင်ချက်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင် LOGEST လုပ်ဆောင်ချက်ကိုအသုံးပြုနည်း
Excel တွင် nonlinear regression လုပ်နည်း
Excel တွင် cubic regression လုပ်ဆောင်နည်း