Excel တွင် prediction interval ကိုဘယ်လိုတည်ဆောက်မလဲ။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်တစ်ခု၊ x နှင့် တုံ့ပြန်မှုကိန်းရှင် y တို့ကြား ဆက်နွယ်မှုကို ကိန်းဂဏန်းသတ်မှတ်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ကျွန်ုပ်တို့သည် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုတစ်ခုကိုလုပ်ဆောင်သောအခါ၊ ကျွန်ုပ်တို့သည် x နှင့် y အကြားဆက်နွယ်မှုကိုဖော်ပြသည့် “ အကောင်းဆုံးစာကြောင်း” ကိုရရှိသည်၊ ၎င်းသည် အောက်ပါအတိုင်းရေးသားနိုင်သည်။

ŷ = b ₀ + b ₁ x

ရွှေ-

• ŷ သည် တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုးဖြစ်သည်။
• b ₀ သည် y-ကြားဖြတ်ဖြစ်သည်။
• b ₁ သည် regression coefficient ဖြစ်သည်။
• x သည် ခန့်မှန်းသူကိန်းရှင်၏တန်ဖိုးဖြစ်သည်။

တစ်ခါတစ်ရံတွင် ကျွန်ုပ်တို့သည် ပေးထားသော x ₀ တန်ဖိုးအတွက် ခန့်မှန်းချက်ကြားကာလ တစ်ခုကို တည်ဆောက်ရန် အကောင်းဆုံးသော ဤမျဉ်းကြောင်းကို အသုံးပြုလိုသည်၊ ထိုသို့သော ခန့်မှန်းတန်ဖိုး ŷ ₀ ပတ်၀န်းကျင်ကြားကာလဖြစ်သည့် လူဦးရေတွင် y ၏ 95% ဖြစ်နိုင်ခြေအမှန်ရှိသည်ဟူသော ဖြစ်နိုင်ခြေရှိသည်။ x ₀ နှင့် သက်ဆိုင်သော ဤကြားကာလတွင် ပါဝင်သည်။

ပေးထားသောတန်ဖိုး x ₀ အတွက် ခန့်မှန်းကြားကာလကို တွက်ချက်ရန်အတွက် ဖော်မြူလာကို ရေးသားထားသည်-

ŷ ₀ +/- t _{α/2၊df=n-2} * se

ရွှေ-

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

ပုံသေနည်းသည် အနည်းငယ် ကြောက်စရာကောင်းပုံရသော်လည်း Excel တွင် တွက်ချက်ရန် အမှန်တကယ် ရိုးရှင်းပါသည်။ ထို့နောက် Excel တွင်ပေးထားသောတန်ဖိုးတစ်ခုအတွက် ခန့်မှန်းကာလတစ်ခုကို တွက်ချက်ရန် ဤဖော်မြူလာကိုအသုံးပြုခြင်း၏ ဥပမာတစ်ခုကို ကျွန်ုပ်တို့တွေ့ရပါမည်။

ဥပမာ- Excel တွင် Prediction Interval တစ်ခုကို တည်ဆောက်ပုံ

အောက်ဖော်ပြပါဒေတာအတွဲတွင် သင်ကြားသည့်နာရီအရေအတွက်နှင့် မတူညီသောကျောင်းသား ၁၅ ဦးမှရရှိသော စာမေးပွဲရမှတ်တို့ကို ပြသသည်-

တန်ဖိုး x ₀ = 3 အတွက် 95% ခန့်မှန်းကြားကာလကို ဖန်တီးလိုသည်ဆိုပါစို့။ ဆိုလိုသည်မှာ၊ လေ့လာနေသော ကျောင်းသားအတွက် စာမေးပွဲရမှတ်သည် ဤကြားကာလအတွင်း ဖြစ်နိုင်ခြေ 95% ရှိကြောင်း ကြားကာလတစ်ခုကို ဖန်တီးလိုပါသည်။ ၃ နာရီ။

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤခန့်မှန်းမှုကြားကာလကို ရရှိရန် လိုအပ်သည့် တန်ဖိုးအားလုံးကို တွက်ချက်ပုံကို ပြသထားသည်။

မှတ်ချက်- ကော်လံ F ရှိ ဖော်မြူလာများသည် ကော်လံ E ရှိ တန်ဖိုးများကို မည်ကဲ့သို့ တွက်ချက်ကြောင်း ပြသသည်။

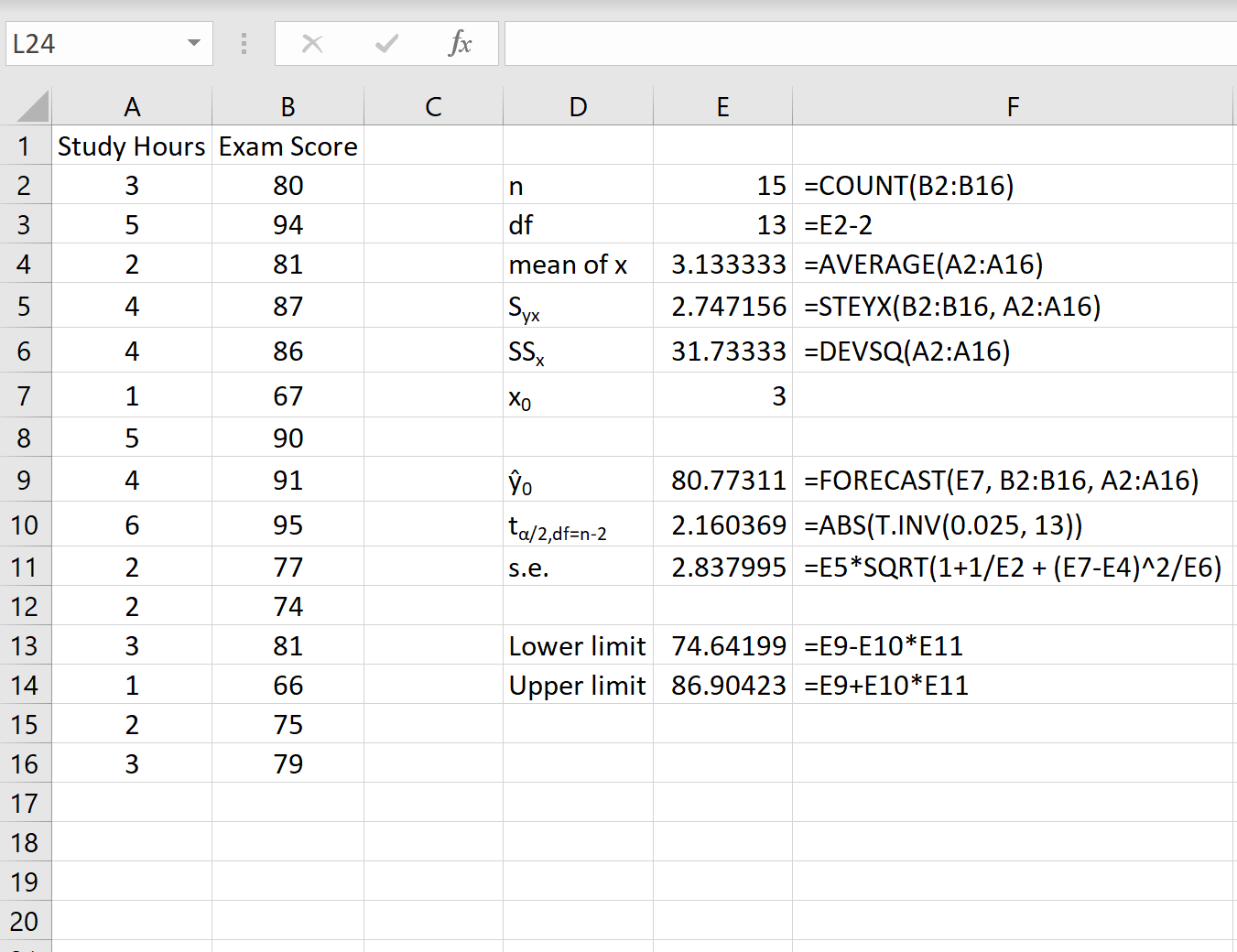
x ₀ = 3 တန်ဖိုးအတွက် 95% ခန့်မှန်းကြားကာလသည် (74.64၊ 86.90) ဖြစ်သည်။ ဆိုလိုသည်မှာ၊ ၃ နာရီကြာလေ့လာသော ကျောင်းသားသည် ၇၄.၆၄ နှင့် ၈၆.၉၀ ကြား ရမှတ်ရရှိရန် ဖြစ်နိုင်ခြေ 95% ဖြင့် ခန့်မှန်းပါသည်။

အသုံးပြုထားသော တွက်ချက်မှုဆိုင်ရာ မှတ်စုအချို့

• t _{α/2၊df=n-2} ၏ t-အရေးပါသောတန်ဖိုးကို တွက်ချက်ရန် ကျွန်ုပ်တို့သည် ခန့်မှန်းကာလ 95% ကို လိုချင်သောကြောင့် α/2 = 0.05/2 = 0.25 ကို အသုံးပြုခဲ့သည်။ ပိုမြင့်သော ခန့်မှန်းကာလများ (ဥပမာ၊ 99% ခန့်မှန်းသည့်ကြားကာလ) သည် ပိုကျယ်သော ကြားကာလများဆီသို့ ဦးတည်သွားမည်ကို သတိပြုပါ။ အပြန်အလှန်အားဖြင့်၊ သေးငယ်သော ခန့်မှန်းကာလ (ဥပမာ 90% ခန့်မှန်းသည့်ကြားကာလ) သည် ပိုကျဉ်းသော ကြားကာလကို ဦးတည်သွားမည်ဖြစ်သည်။
• ကျွန်ုပ်တို့သည် ŷ ₀ အတွက် ခန့်မှန်းတန်ဖိုးကိုရရှိရန် ဖော်မြူလာ =FORECAST() ကို အသုံးပြုခဲ့သော်လည်း ဖော်မြူလာ =FORECAST.LINEAR() သည် အတိအကျတူညီသောတန်ဖိုးကို ပြန်ပေးမည်ဖြစ်သည်။