Excel တွင် mean ၏ standard error တွက်ချက်နည်း

ပျမ်းမျှအမှား သည် ဒေတာအစုတစ်ခုအတွင်း တန်ဖိုးများ ဖြန့်ဖြူးမှုကို တိုင်းတာသည့်နည်းလမ်းဖြစ်သည်။ အောက်ပါအတိုင်း တွက်ချက်သည်။

စံအမှား = s / √n

ရွှေ-

• s : နမူနာစံသွေဖည်
• n : နမူနာအရွယ်အစား

အောက်ပါဖော်မြူလာကို အသုံးပြု၍ Excel ရှိ မည်သည့်ဒေတာသတ်မှတ်မှုမဆို ပျမ်းမျှအမှား၏ စံအမှားကို တွက်ချက်နိုင်သည်။

= STDEV (တန်ဖိုးများ အပိုင်းအခြား) / SQRT ( COUNT (တန်ဖိုးများ အပိုင်းအခြား))

အောက်ဖော်ပြပါ ဥပမာသည် ဤဖော်မြူလာကို အသုံးပြုနည်းကို ပြသထားသည်။

ဥပမာ- Excel တွင် ပုံမှန်အမှား

ကျွန်ုပ်တို့တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

အောက်ဖော်ပြပါ ဖန်သားပြင်ဓာတ်ပုံသည် ဤဒေတာအတွဲအတွက် ပျမ်းမျှအမှားကို တွက်ချက်နည်းကို ပြသသည်-

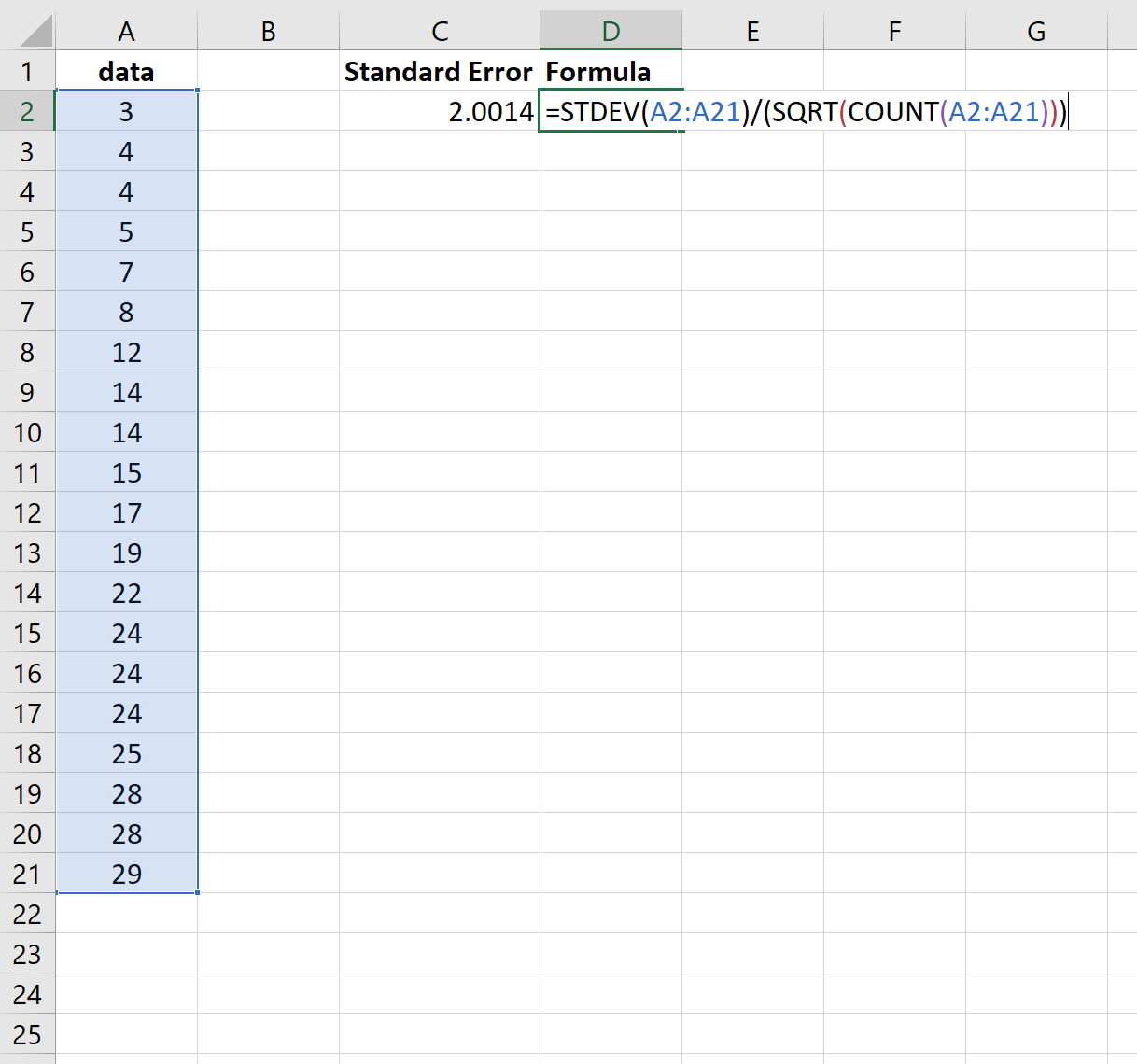
စံအမှားသည် 2.0014 ဖြစ်လာသည်။

=STDEV() လုပ်ဆောင်ချက်သည် Excel ရှိ =STDEV.S() လုပ်ဆောင်ချက်နှင့် ညီမျှသော နမူနာဆိုလိုချက်ကို တွက်ချက်ကြောင်း သတိပြုပါ။

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် တူညီသောရလဒ်များရရှိရန် အောက်ပါဖော်မြူလာကို အသုံးပြု၍ရနိုင်သည်-

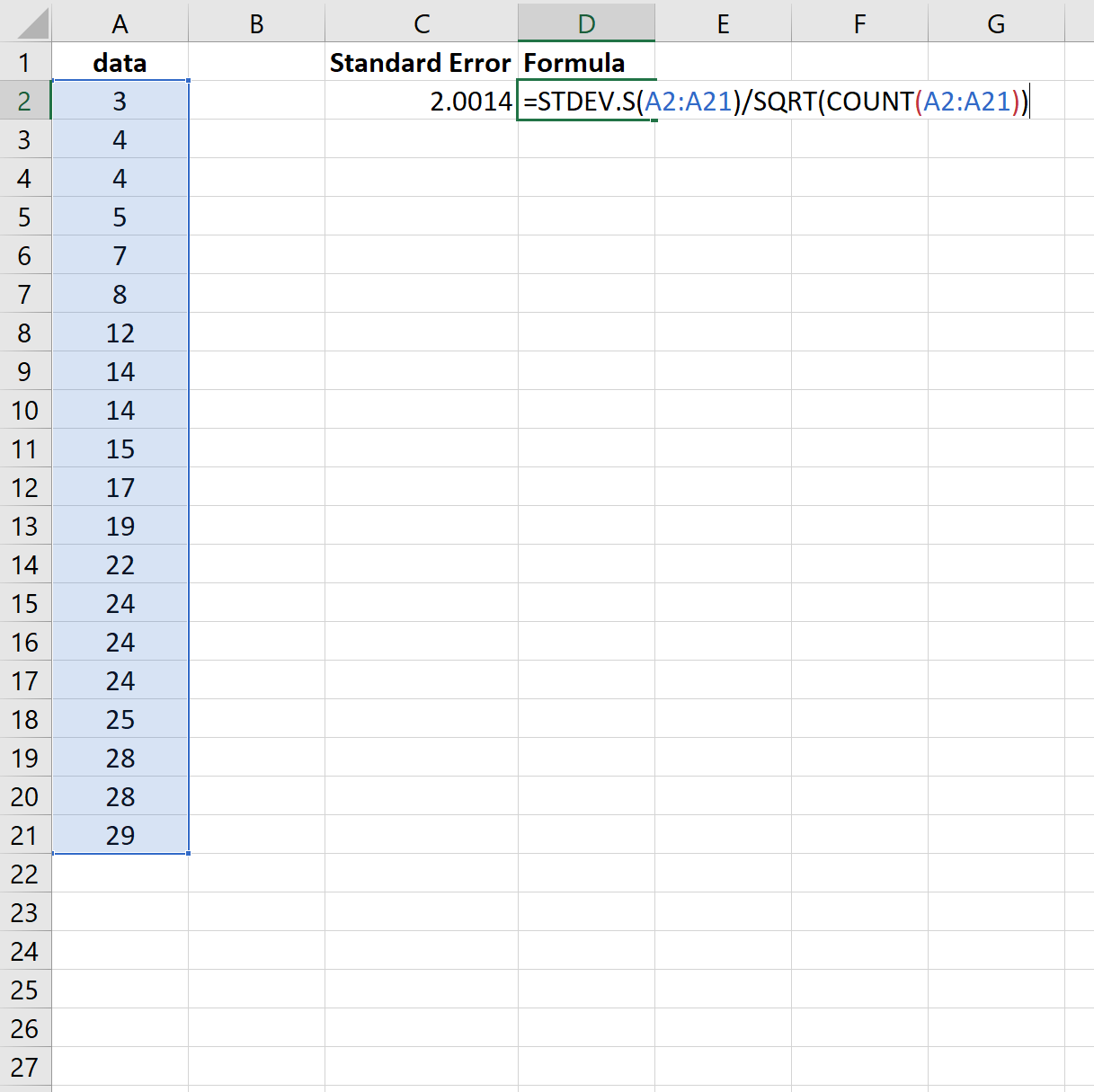
တစ်ဖန်၊ စံအမှားသည် 2.0014 ဖြစ်လာသည်။

ဆိုလိုရင်း၏ စံအမှားကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံ

ဆိုလိုရင်း၏ စံအမှားသည် ပျမ်းမျှအားဖြင့် တန်ဖိုးများ ပျံ့နှံ့မှုကို တိုင်းတာခြင်း ဖြစ်သည်။ ဆိုလိုရင်း၏ စံအမှားကို ဘာသာပြန်ရာတွင် သတိပြုရမည့်အချက် နှစ်ခုရှိသည်။

1. mean ၏ standard error ကြီးလေ၊ data set တစ်ခုတွင် mean ဝန်းကျင်တန်ဖိုးများ ပိုမိုပြန့်ကျဲလေဖြစ်သည်။

၎င်းကို သရုပ်ဖော်ရန်၊ ကျွန်ုပ်တို့သည် ယခင်ဒေတာအတွဲ၏ နောက်ဆုံးတန်ဖိုးကို ပိုမိုကြီးမားသော နံပါတ်ဖြင့် ပြောင်းလဲမည်ကို သုံးသပ်ပါ-

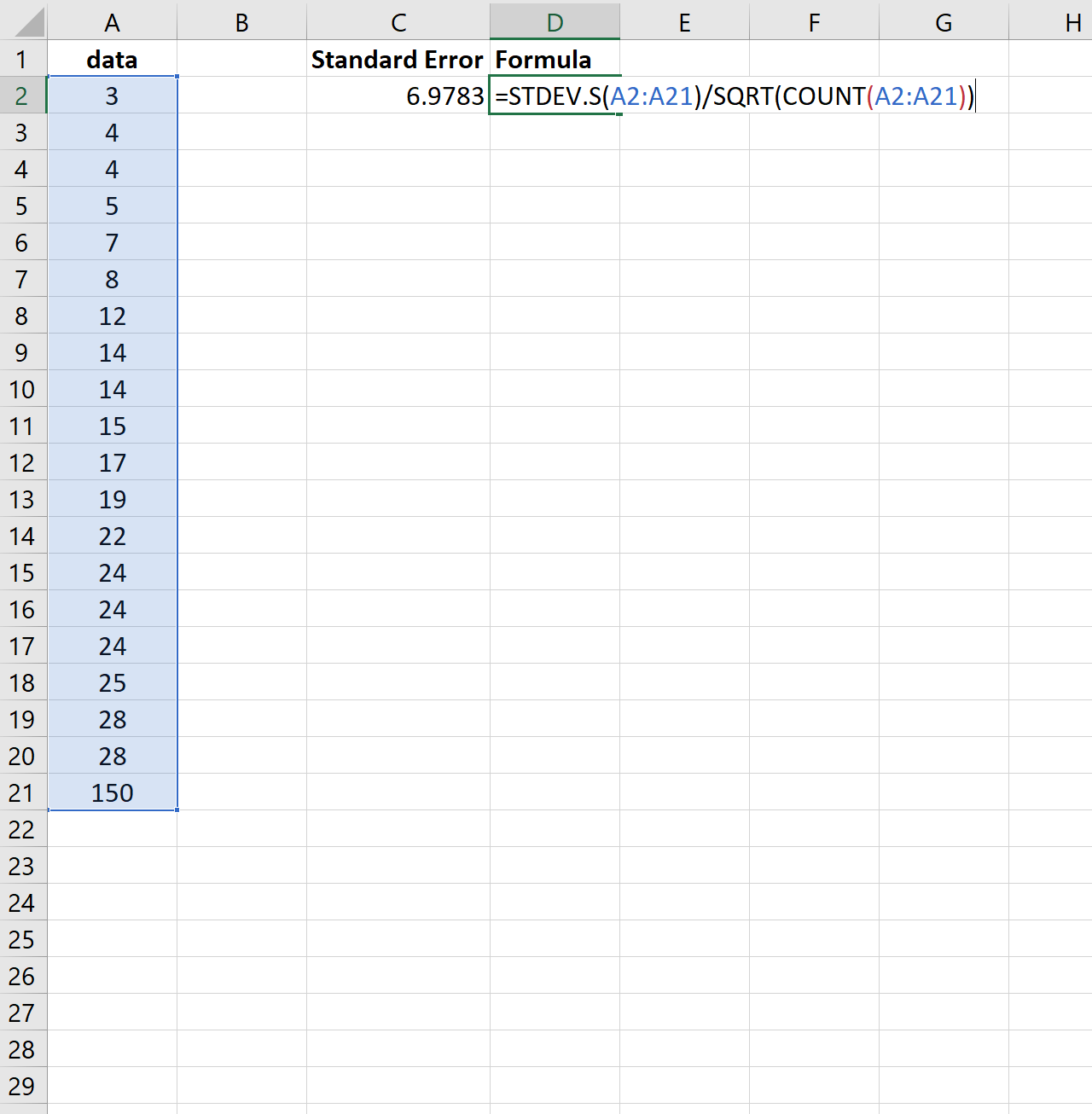
စံအမှားသည် 2.0014 မှ 6.9783 သို့ မည်သို့တိုးလာသည်ကို သတိပြုပါ။ ဤဒေတာအတွဲရှိ တန်ဖိုးများသည် ယခင်ဒေတာအတွဲနှင့် နှိုင်းယှဉ်ပါက ပျမ်းမျှတစ်ဝိုက်တွင် ပိုမိုဖြန့်ဝေကြောင်း ညွှန်ပြသည်။

2. နမူနာအရွယ်အစား တိုးလာသည်နှင့်အမျှ ဆိုလိုရင်း၏ စံအမှားသည် လျော့နည်းသွားတတ်သည်။

ယင်းကို သရုပ်ဖော်ရန်၊ အောက်ပါဒေတာနှစ်စုံအတွက် ဆိုလိုရင်း၏ စံအမှားကို သုံးသပ်ကြည့်ပါ-

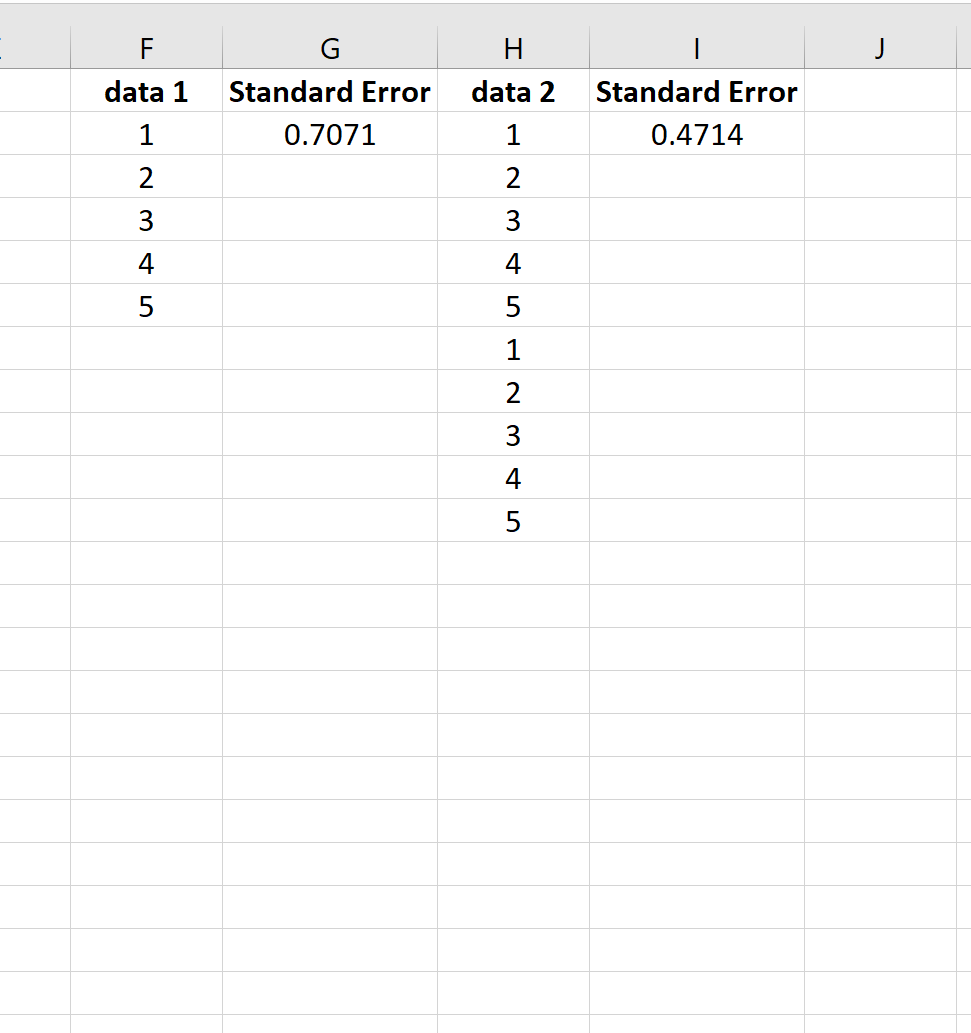
ဒုတိယဒေတာအတွဲသည် ပထမဒေတာအတွဲကို နှစ်ကြိမ်ထပ်ခါထပ်ခါပြုလုပ်ခြင်းဖြစ်သည်။ ထို့ကြောင့် ဒေတာအတွဲနှစ်ခုစလုံးသည် တူညီသောအဓိပ္ပာယ်ရှိသော်လည်း ဒုတိယဒေတာအတွဲသည် ပိုကြီးသောနမူနာအရွယ်အစားရှိပြီး ထို့ကြောင့် စံအမှားတစ်ခုရှိသည်။