Excel တွင် normalcdf probabilities ကို တွက်ချက်နည်း

TI-83 သို့မဟုတ် TI-84 ဂဏန်းတွက်စက်ပေါ်ရှိ NormalCDF လုပ်ဆောင်ချက်ကို ပုံမှန်ဖြန့်ဝေထားသော ကျပန်းကိန်းရှင်သည် အချို့သောအကွာအဝေးအတွင်း တန်ဖိုးတစ်ခုယူနိုင်သည့် ဖြစ်နိုင်ခြေကို ရှာဖွေရန် အသုံးပြုနိုင်သည်။

TI-83 သို့မဟုတ် TI-84 ဂဏန်းတွက်စက်တွင်၊ ဤလုပ်ဆောင်ချက်သည် အောက်ပါ syntax ကိုအသုံးပြုသည်။

normalcdf (အောက်၊ အထက်၊ μ၊ σ)

ရွှေ-

• lower = အပိုင်းအခြား၏ တန်ဖိုးနိမ့်
• upper = အပိုင်းအခြား၏ အထက်တန်ဖိုး
• µ = လူဦးရေကို ဆိုလိုသည်။
• σ = လူဦးရေစံသွေဖည်

ဥပမာအားဖြင့်၊ ကျပန်းကိန်းရှင်တစ်ခုအား ပုံမှန်အားဖြင့် ပျမ်းမျှအားဖြင့် 50 နှင့် 4 ၏ စံသွေဖည်မှုဖြင့် ဖြန့်ဝေသည် ဆိုပါစို့။ 48 နှင့် 52 ကြားတန်ဖိုးကိုယူပြီး ကျပန်းကိန်းရှင်၏ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

normalcdf(48၊ 52၊ 50၊ 4) = 0.3829

အောက်ပါ syntax ကိုအသုံးပြုသည့် NORM.DIST() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဤတုံ့ပြန်ချက်ကို Excel တွင် ပြန်လည်ထုတ်လုပ်နိုင်သည်-

NORM.DIST(x၊ σ၊ μ၊ စုစည်းမှု)

ရွှေ-

• x = တစ်ဦးချင်းဒေတာတန်ဖိုး
• µ = လူဦးရေကို ဆိုလိုသည်။
• σ = လူဦးရေစံသွေဖည်
• စုစည်းမှု = မှားယွင်းသော PDF တွက်ချက်မှု; TRUE သည် CDF ကို တွက်ချက်သည်။

အောက်ဖော်ပြပါ ဥပမာများသည် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

ဥပမာ 1- တန်ဖိုးနှစ်ခုကြားဖြစ်နိုင်ခြေ

ကျပန်း variable တစ်ခုကို ပုံမှန်အားဖြင့် mean of 50 နှင့် 4 ၏ standard deviation တစ်ခုဖြင့် ဖြန့်ဝေသည်ဆိုပါစို့။ 48 နှင့် 52 ကြား တန်ဖိုးကိုယူပြီး ကျပန်း variable ၏ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

အောက်ဖော်ပြပါပုံသည် Excel တွင်ဤတွက်ချက်နည်းကိုပြသသည်-

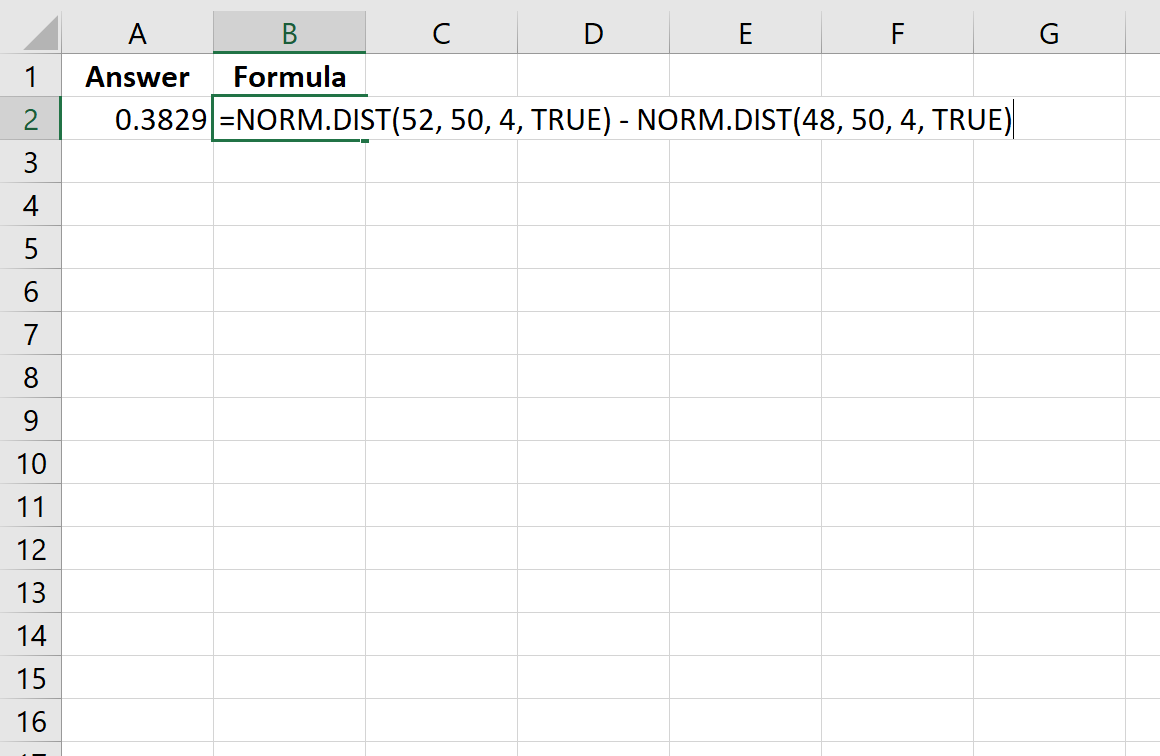
ဖြစ်နိုင်ခြေသည် 0.3829 ဖြစ်လာသည်။

ဥပမာ 2- တန်ဖိုးတစ်ခုထက်နည်းသော ဖြစ်နိုင်ခြေ

ကျပန်း variable တစ်ခုကို ပုံမှန်အားဖြင့် mean of 50 နှင့် 4 ၏ standard deviation ဖြင့် ဖြန့်ဝေသည်ဆိုပါစို့။ 48 ထက်နည်းသော value ကိုယူသော ကျပန်း variable ၏ ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

 =NORM. DIST (48, 50, 4, TRUE )

အောက်ဖော်ပြပါပုံသည် Excel တွင်ဤတွက်ချက်နည်းကိုပြသသည်-

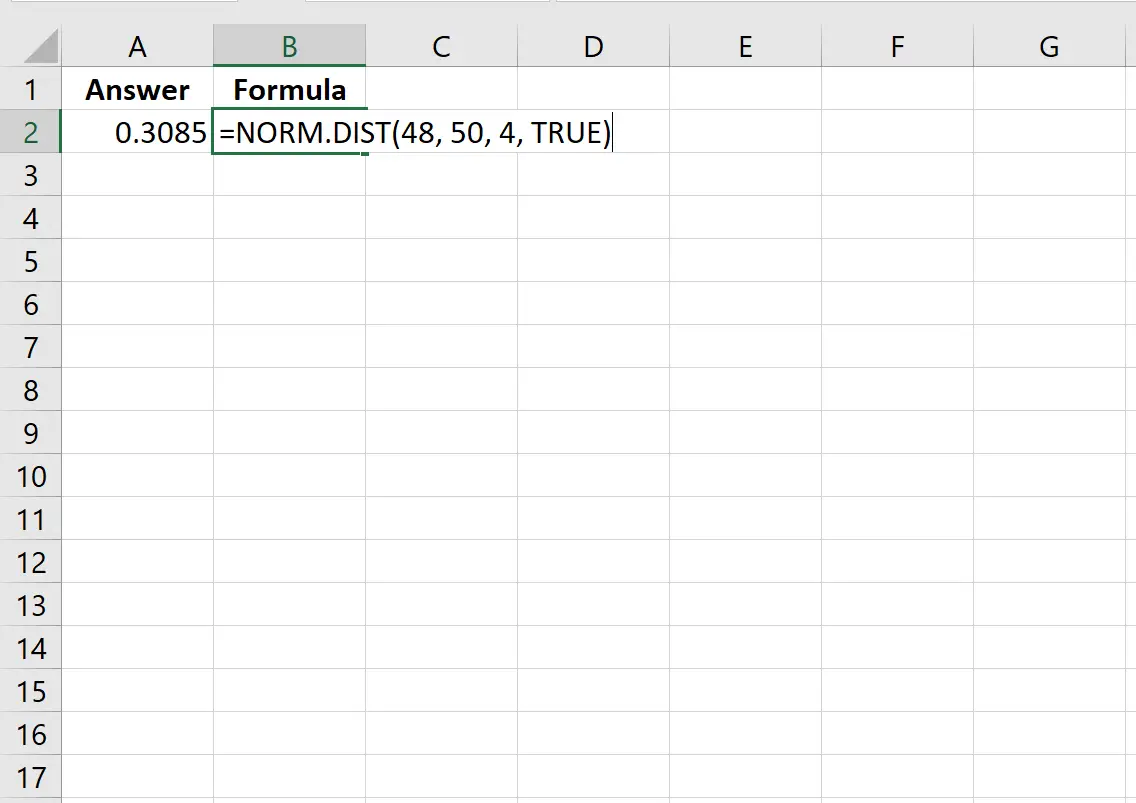
ဖြစ်နိုင်ခြေသည် 0.3085 ဖြစ်သွားသည်။

ဥပမာ 3- တန်ဖိုးထက် ဖြစ်နိုင်ခြေပိုများသည်။

ကျပန်းကိန်းရှင်တစ်ခုအား ပျမ်းမျှအားဖြင့် 50 နှင့် 4 ၏ စံသွေဖည်မှုဖြင့် ဖြန့်ဝေသည်ဆိုပါစို့။ 55 ထက်ကြီးသော တန်ဖိုးကိုယူသောကျပန်းကိန်းရှင်၏ဖြစ်နိုင်ခြေကို အောက်ပါအတိုင်းတွက်ချက်နိုင်ပါသည်။

 =1 - NORM. DIST (55, 50, 4, TRUE )

အောက်ဖော်ပြပါပုံသည် Excel တွင်ဤတွက်ချက်နည်းကိုပြသသည်-

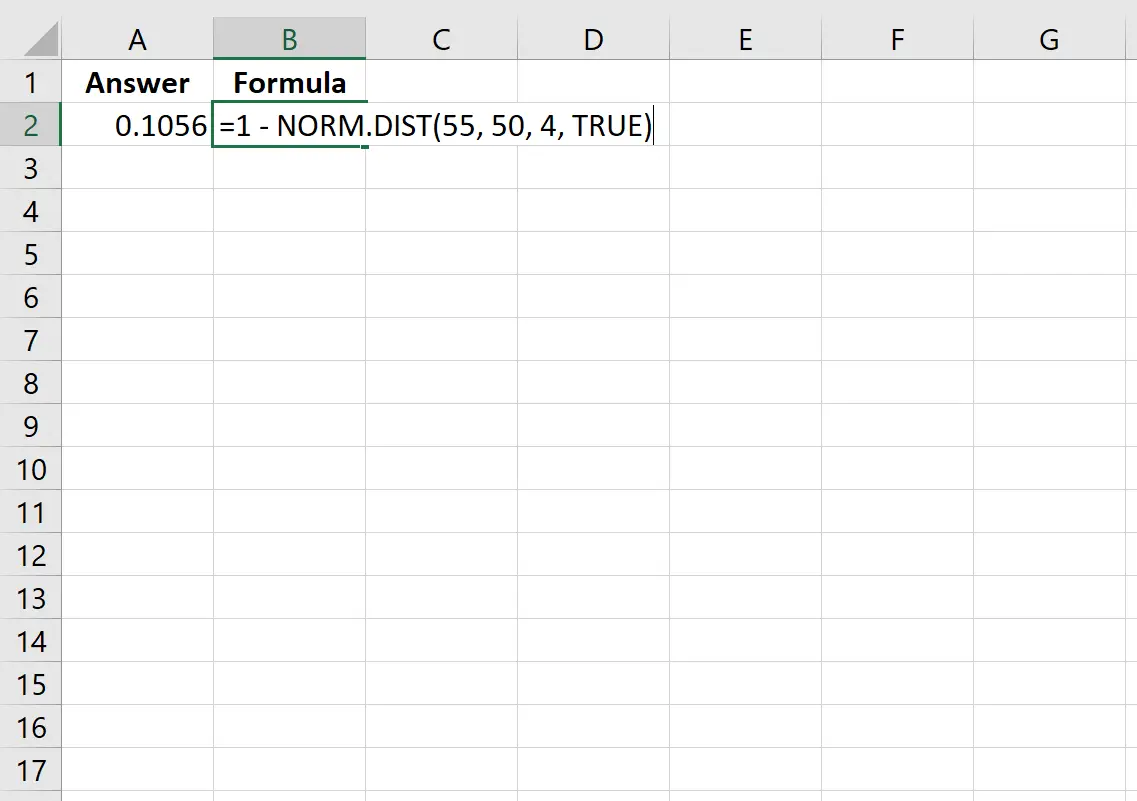
ဖြစ်နိုင်ခြေသည် 0.1056 ဖြစ်သွားသည်။

ထပ်လောင်းအရင်းအမြစ်များ

သင်သည် ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခုနှင့်ဆက်စပ်သော ဖြစ်နိုင်ခြေများကို အလိုအလျောက်ရှာဖွေရန် ဤ ပုံမှန် CDF ဂဏန်းတွက်စက် ကိုလည်း သင်အသုံးပြုနိုင်ပါသည်။