Excel တွင် exponential distribution ကိုအသုံးပြုနည်း

ကိန်းဂဏန်းဖြန့်ချီမှုသည် အချို့သောဖြစ်ရပ်တစ်ခုဖြစ်ပေါ်သည်အထိ ကျွန်ုပ်တို့စောင့်ဆိုင်းရမည့်အချိန်ကို နမူနာယူရန် အသုံးပြုသည့် ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ဤကဲ့သို့သော ဖြန့်ဝေမှုအား မေးခွန်းများဖြေဆိုရန်အတွက် အသုံးပြုနိုင်ပါသည်။

• လက်လီရောင်းချသူတစ်ဦးသည် ဖောက်သည်တစ်ဦး၏စတိုးဆိုင်သို့ ဝင်ရောက်ရန် အချိန်မည်မျှစောင့်သင့်သနည်း။
• ဘက်ထရီမသေဆုံးမီ အချိန်မည်မျှကြာအောင် ဆက်လက်လုပ်ဆောင်နိုင်မည်နည်း။
• ကွန်ပြူတာ မပြိုကွဲမီ အချိန်မည်မျှကြာအောင် ဆက်လက်လုပ်ဆောင်နိုင်မည်နည်း။

အခြေအနေတစ်ခုစီတွင်၊ အချို့သောဖြစ်ရပ်တစ်ခုဖြစ်ပေါ်လာသည်အထိ ကျွန်ုပ်တို့စောင့်ဆိုင်းရမည့်အချိန်ကို တွက်ချက်လိုပါသည်။ ထို့ကြောင့်၊ ဇာတ်ညွှန်းတစ်ခုစီကို ကိန်းဂဏန်းဖြန့်ချီမှုတစ်ခုကို အသုံးပြု၍ စံနမူနာယူနိုင်သည်။

ကျပန်းပြောင်းလဲနိုင်သော X သည် ကိန်းဂဏန်းဖြန့်ချီမှုတစ်ခုနောက်လိုက်ပါက၊ X ၏ စုစည်းသိပ်သည်းမှုလုပ်ဆောင်ချက်ကို ရေးသားနိုင်သည်-

F (x; λ) = 1 – e ^–λx

ရွှေ-

• λ- နှုန်းသတ်မှတ်ချက် (λ = 1/μ အဖြစ် တွက်ချက်)
• e- ခန့်မှန်းခြေ ကိန်းသေတစ်ခုသည် 2.718 နှင့် ညီမျှသည်။

Excel ရှိ exponential ဖြန့်ချီမှု၏ စုစည်းသိပ်သည်းဆ လုပ်ဆောင်မှုဆိုင်ရာ ဖြစ်နိုင်ခြေများကို တွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

 =EXPON.DIST(x, lambda, cumulative)

ရွှေ-

• x : ထပ်ကိန်းခွဲဝေထားသော ကျပန်းပြောင်းလဲနိုင်သောတန်ဖိုး
• lambda : နှုန်းသတ်မှတ်ချက်
• စုစည်းမှု – စုစည်းသိပ်သည်းမှု လုပ်ဆောင်ချက် (အမှန် သို့မဟုတ် မှား) ကို အသုံးပြုခြင်း ရှိ၊ မရှိ၊

အောက်ဖော်ပြပါ ဥပမာများသည် ဤဖော်မြူလာကို လက်တွေ့တွင် အသုံးပြုနည်းကို ပြသထားသည်။

ဥပမာ 1- နောက်ဖောက်သည် မရောက်မချင်း အချိန်

ဖောက်သည်အသစ်သည် ပျမ်းမျှအားဖြင့် နှစ်မိနစ်တိုင်း စတိုးဆိုင်သို့ ဝင်သည်။ ဖောက်သည်ရောက်လာပြီးနောက် တစ်မိနစ်အတွင်း ဖောက်သည်အသစ်ရောက်ရှိလာမည့် ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ပါ။

ဖြေရှင်းချက်- သုံးစွဲသူများကြား ပျမ်းမျှအချိန်သည် နှစ်မိနစ်ဖြစ်သည်။ ထို့ကြောင့် နှုန်းထားကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်။

• λ = 1/µ
• λ = 1/2
• λ = 0.5

ထို့ကြောင့်၊ တစ်မိနစ်အတွင်း ဖောက်သည်အသစ်ရောက်ရှိလာနိုင်ခြေကို တွက်ချက်ရန် Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်သည်။

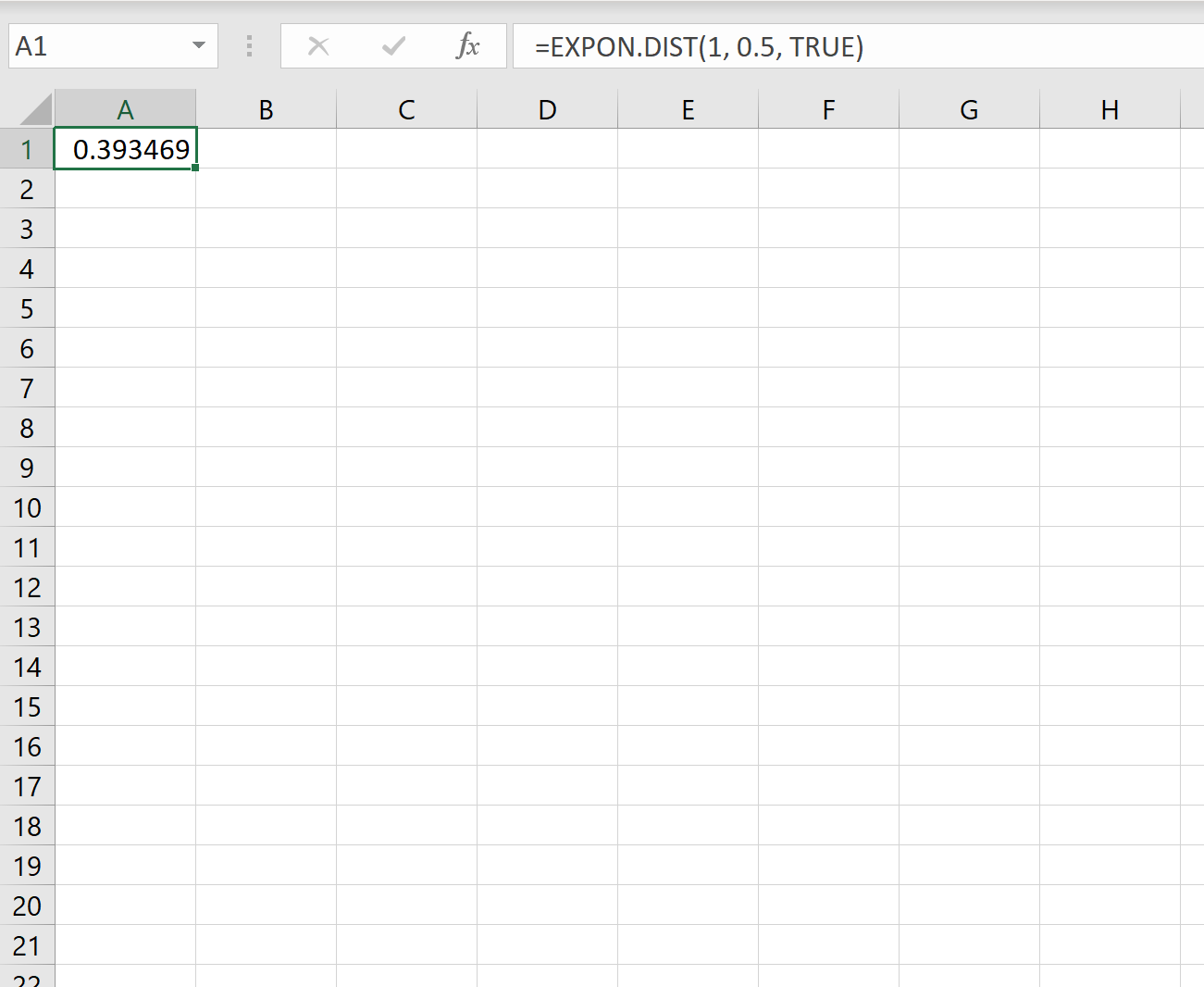
နောက်ထပ်ဝယ်ယူသူရောက်လာရန် တစ်မိနစ်ထက်မနည်း စောင့်ရရမည့်ဖြစ်နိုင်ခြေမှာ 0.393469 ဖြစ်သည်။

ဥပမာ 2- နောက်တစ်ကြိမ် ငလျင်လှုပ်မည့်အချိန်

နေရာဒေသတစ်ခုတွင် ရက်ပေါင်း 400 လျှင် ပျမ်းမျှ ငလျင်တစ်ခု ဖြစ်ပေါ်သည်ဆိုပါစို့။ ငလျင်လှုပ်ပြီးနောက် နောက်ငလျင်မလှုပ်မီ ရက်ပေါင်း 500 ထက် ပိုဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ပါ။

ဖြေရှင်းချက်- ငလျင်လှုပ်ခတ်မှုအကြား ပျမ်းမျှအချိန်သည် ရက်ပေါင်း ၄၀၀ ဖြစ်သည်။ ထို့ကြောင့် နှုန်းထားကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်။

• λ = 1/µ
• λ = 1/400
• λ = 0.0025

ထို့ကြောင့်၊ နောက်တစ်ကြိမ် ငလျင်ဖြစ်ပေါ်ရန် ရက်ပေါင်း 500 ထက်နည်းသော ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် Excel တွင် အောက်ပါပုံသေနည်းကို အသုံးပြုနိုင်ပါသည်။

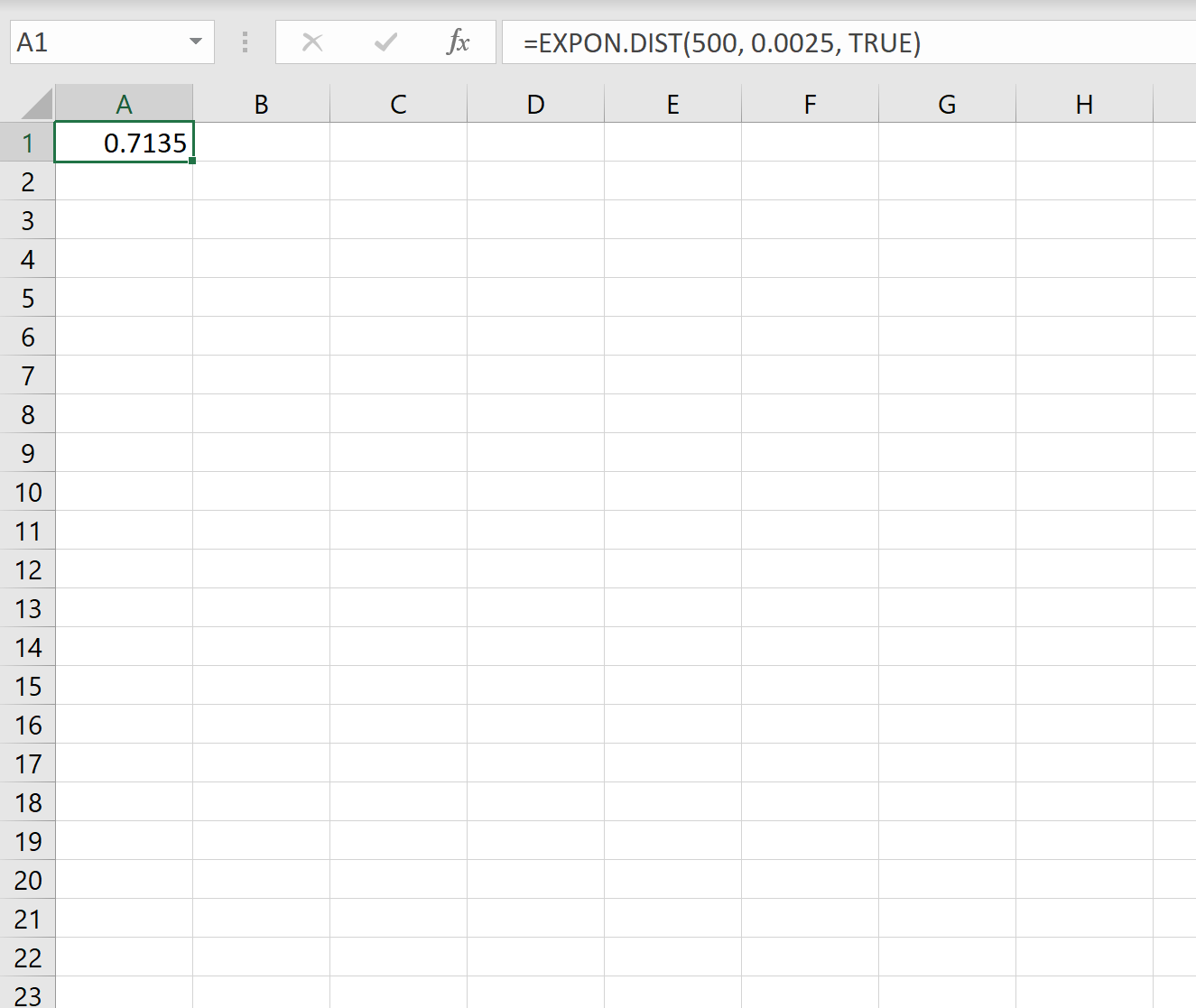
နောက်တစ်ကြိမ် ငလျင်မလှုပ်မီ ရက်ပေါင်း 500 ထက်နည်းသော ဖြစ်နိုင်ခြေမှာ 0.7135 ဖြစ်သည်။

ဒါကြောင့် နောက်တစ်ကြိမ် ငလျင်အတွက် ရက်ပေါင်း 500 ကျော် စောင့်ရမယ့် ဖြစ်နိုင်ခြေက 1 – 0.7135 = 0.2865 ဖြစ်ပါတယ်။

ဥပမာ 3- နောက်တစ်ကြိမ် ဖုန်းခေါ်ဆိုမှုအထိ အချိန်

ခေါ်ဆိုမှုစင်တာတစ်ခုသည် ပျမ်းမျှအားဖြင့် 10 မိနစ်တိုင်း ခေါ်ဆိုမှုအသစ်တစ်ခုရရှိသည်ဆိုပါစို့။ ဖောက်သည်တစ်ဦးဖုန်းခေါ်ဆိုပြီးနောက် 10 မိနစ်မှ 15 မိနစ်အတွင်း ဖောက်သည်အသစ်တစ်ဦးခေါ်ဆိုမည့်ဖြစ်နိုင်ခြေကို ဆုံးဖြတ်ပါ။

ဖြေရှင်းချက်- ဖုန်းခေါ်ဆိုမှုအကြား ပျမ်းမျှအချိန်သည် 10 မိနစ်ဖြစ်သည်။ ထို့ကြောင့် နှုန်းထားကို အောက်ပါအတိုင်း တွက်ချက်နိုင်သည်။

• λ = 1/µ
• λ = 1/10
• λ = 0.1

ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် 10 မှ 15 မိနစ်အတွင်း ခေါ်ဆိုမည့် ဖြစ်နိုင်ခြေကို တွက်ချက်ရန် Excel တွင် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

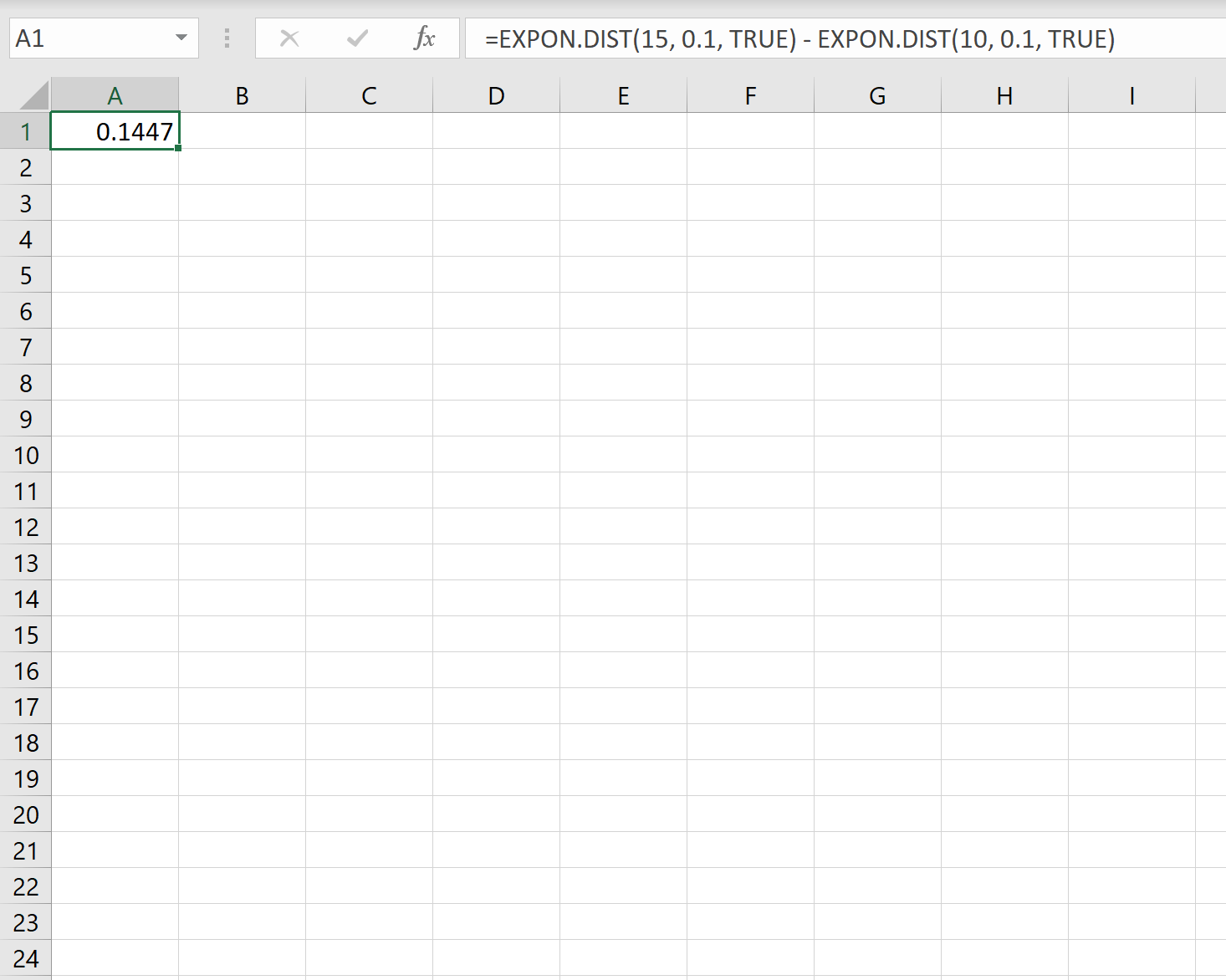
ဖောက်သည်အသစ်သည် 10-15 မိနစ်အတွင်း ဖုန်းခေါ်မည့်အလားအလာ။ 0.1447 ဖြစ်ပါတယ်။

ထပ်လောင်းအရင်းအမြစ်များ

Exponential Distribution နိဒါန်း
ကိန်းဂဏန်းဖြန့်ချီမှု၏ မှတ်ဉာဏ်မဲ့ပိုင်ဆိုင်မှု
R တွင် ကိန်းဂဏန်းဖြန့်ချီမှုတစ်ခုကို မည်သို့ဆွဲမည်နည်း။