F1 ရမှတ်နှင့် တိကျမှု- မည်သည့်အရာကို အသုံးပြုသင့်သနည်း။
စက်သင်ယူမှုတွင် အမျိုးအစားခွဲခြင်းပုံစံများကို အသုံးပြုသည့်အခါ၊ မော်ဒယ်အရည်အသွေးကို အကဲဖြတ်ရန် ကျွန်ုပ်တို့အသုံးပြုလေ့ရှိသည့် မက်ထရစ်နှစ်ခုမှာ F1 ရမှတ် နှင့် တိကျမှု ဖြစ်သည်။
မက်ထရစ်နှစ်ခုလုံးအတွက်၊ တန်ဖိုးပိုမြင့်လေ၊ လေ့လာမှုများကို အတန်းများအဖြစ် အမျိုးအစားခွဲခြားနိုင်သော မော်ဒယ်တစ်ခုသည် ပို၍လုပ်ဆောင်နိုင်လေဖြစ်သည်။
သို့ရာတွင်၊ မက်ထရစ်တစ်ခုစီကို မတူညီသောဖော်မြူလာတစ်ခုဖြင့် တွက်ချက်ထားပြီး ၎င်းကိုအသုံးပြုရာတွင် အားသာချက်များနှင့် အားနည်းချက်များရှိသည်။
အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့တွင် မက်ထရစ်တစ်ခုစီကို တွက်ချက်နည်းကို ပြသထားသည်။
ဥပမာ- F1 ရမှတ်နှင့် တိကျမှုကို တွက်ချက်ခြင်း။
မတူညီသောကောလိပ်ဘတ်စကက်ဘောကစားသမား 400 ကို NBA သို့ရေးဆွဲမည်လား မခန့်မှန်းရန် ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့အသုံးပြုသည်ဆိုပါစို့။
အောက်ဖော်ပြပါ ရှုပ်ထွေးမှု matrix သည် မော်ဒယ်မှ ပြုလုပ်သော ခန့်မှန်းချက်များကို အကျဉ်းချုပ်ဖော်ပြသည်-
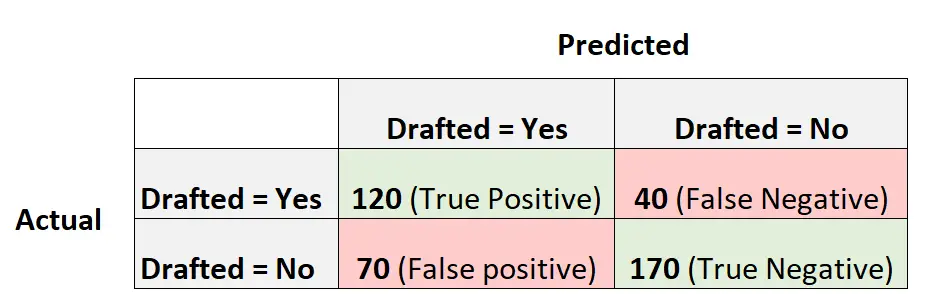
ဤသည်မှာ ရှုပ်ထွေးမှုမက်ထရစ်အတွက် အမျိုးမျိုးသော မက်ထရစ်များကို တွက်ချက်နည်းဖြစ်သည်။
တိကျမှု- စုစုပေါင်း အပြုသဘောဆောင်သော ခန့်မှန်းချက်များနှင့် ဆက်စပ်သော အပြုသဘောဆောင်သော ခန့်မှန်းချက်များ မှန်ကန်ပါသည်။
- တိကျမှု = True Positive / (True Positive + False Positive)
- တိကျမှု = 120/(120+70)၊
- တိကျမှု = 0.63
သတိပေးချက်- စုစုပေါင်းအမှန်တကယ် အပြုသဘောဆောင်မှုများနှင့် ပတ်သက်၍ အပြုသဘောဆောင်သော ခန့်မှန်းချက်များကို ပြင်ပါ။
- ပြန်လည်ခေါ်ဆိုခြင်း = စစ်မှန်သော အပြုသဘောဆောင်ခြင်း / (မှန်ကန်သော အပြုသဘော + မှားယွင်းသော အနုတ်လက္ခဏာ)
- မိသ = ၁၂၀/(၁၂၀+၄၀)၊
- ပြန်လည်သိမ်းဆည်းခြင်း = 0.75
တိကျမှု- လေ့လာတွေ့ရှိချက်အားလုံး၏ ရာခိုင်နှုန်းကို မှန်ကန်စွာ ခွဲခြားထားသည်။
- တိကျမှု = (အကောင်းမြင် + အစစ်အမှန် အနှုတ်) / (စုစုပေါင်း နမူနာအရွယ်အစား)
- တိကျမှု = (၁၂၀ + ၁၇၀) / (၄၀၀)၊
- တိကျမှု = 0.725
F1 ရမှတ်- တိကျမှုနှင့် ပြန်လည်သိမ်းဆည်းမှု၏ ဟာမိုနစ်ပျမ်းမျှ
- F1 ရမှတ် = 2 * (တိကျမှု * ပြန်လည်ခေါ်ယူခြင်း) / (တိကျမှု + ပြန်လည်ခေါ်ယူခြင်း)
- F1 ရမှတ် = 2 * (0.63 * 0.75) / (0.63 + 0.75)၊
- F1 ရမှတ် = 0.685
F1 ရမှတ်နှင့် တိကျမှုကို မည်သည့်အချိန်တွင် အသုံးပြုရမည်နည်း။
F1 ရမှတ်နှင့် တိကျမှုကို အသုံးပြုခြင်းတွင် ကောင်းကျိုးနှင့် ဆိုးကျိုးများ ရှိပါသည်။
တိကျမှု
Pro : ဘာသာပြန်ရန် လွယ်ကူသည်။ မော်ဒယ်တစ်ခုသည် 90% တိကျသည်ဟု ဆိုပါက၊ ၎င်းသည် လေ့လာတွေ့ရှိချက်များ၏ 90% ကို မှန်ကန်စွာ ခွဲခြားထားကြောင်း ကျွန်ုပ်တို့သိပါသည်။
အားနည်းချက် – ဒေတာဖြန့်ဝေပုံကို ထည့်မတွက်ပါ။ ဥပမာအားဖြင့်၊ ကစားသမားအားလုံး၏ 90% သည် NBA သို့မသတ်မှတ်ထားကြောင်း ယူဆကြပါစို့။ အကယ်၍ ကစားသမားတိုင်းသည် အကြမ်းမဖက်ဘဲနေမည်ဟု ရိုးရိုးရှင်းရှင်း ခန့်မှန်းထားသည့် မော်ဒယ်တစ်ခုရှိလျှင် မော်ဒယ်သည် ကစားသမားများ၏ 90% အတွက် ရလဒ်ကို မှန်ကန်စွာ ခန့်မှန်းပေးမည်ဖြစ်သည်။ ဤတန်ဖိုးသည် မြင့်မားပုံရသည်၊ သို့သော် မည်သည့်ကစားသမားများ ရေးဆွဲမည်ကို မှန်ကန်စွာ ခန့်မှန်း၍မရသော မော်ဒယ်ဖြစ်သည်။
F1 ရလဒ်များ
Pro : ဒေတာဖြန့်ဝေပုံကို သုံးသပ်ကြည့်ပါ။ ဥပမာအားဖြင့်၊ ဒေတာသည် အလွန်မျှတမှုမရှိပါက (ဥပမာ ကစားသမားအားလုံး၏ 90% သည် မရေးဆွဲရသေးဘဲ 10% ဖြစ်သည်)၊ ထို့နောက် F1 ရမှတ်သည် မော်ဒယ်၏စွမ်းဆောင်ရည်ကို ပိုမိုကောင်းမွန်စွာ အကဲဖြတ်ပေးမည်ဖြစ်ပါသည်။
အားနည်းချက် – အဓိပ္ပာယ်ဖွင့်ဆိုရန် ပိုခက်ခဲသည်။ F1 ရမှတ်သည် တိကျမှုနှင့် မော်ဒယ်ပြန်လည်သိမ်းဆည်းမှုတို့ ရောနှောထားသောကြောင့် အဓိပ္ပာယ်ဖွင့်ဆိုရန် အနည်းငယ်ပိုခက်ခဲစေသည်။
ယေဘုယျအားဖြင့်-
အတန်းများ မျှတပြီး မှားယွင်းသော အနုတ်လက္ခဏာများကို ခန့်မှန်းခြင်းအတွက် ကြီးကြီးမားမား အားနည်းချက်မရှိသည့်အခါ ကျွန်ုပ်တို့သည် တိကျမှုကို အသုံးပြုလေ့ရှိသည်။
အတန်းများ ဟန်ချက်မညီဘဲ မှားယွင်းသော အနုတ်လက္ခဏာများကို ခန့်မှန်းရာတွင် ဆိုးရွားသော အားနည်းချက်တစ်ခု ရှိနေသောအခါတွင် ကျွန်ုပ်တို့သည် F1 ရမှတ်ကို အသုံးပြုလေ့ရှိသည်။
ဥပမာအားဖြင့်၊ လူတစ်ဦးတွင် ကင်ဆာရှိ/မရှိကို ခန့်မှန်းရန် ထောက်ပံ့ပို့ဆောင်ရေးဆိုင်ရာ ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုပါက၊ မှားယွင်းသောအနုတ်လက္ခဏာများသည် အမှန်တကယ်ဆိုးရွားသည် (ဥပမာ- လူတစ်ဦးတွင် အမှန်တကယ်ကင်ဆာမရှိဟု ခန့်မှန်းခြင်း) ထို့ကြောင့် F1 ရမှတ်သည် မော်ဒယ်များကို အပြစ်ပေးမည်ဖြစ်သည်။ false negatives တွေ အရမ်းများတယ်။ တိကျမှုထက် ပိုပါတယ်။
ထပ်လောင်းအရင်းအမြစ်များ
ဆုတ်ယုတ်မှု vs. အမျိုးအစားခွဲခြားခြင်း- ကွာခြားချက်ကား အဘယ်နည်း။
Logistic Regression နိဒါန်း
R တွင် logistic regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း
Python တွင် Logistic Regression ကို မည်သို့လုပ်ဆောင်မည်နည်း။