Excel တွင် friedman test ကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။

Friedman စမ်းသပ်မှု သည် ANOVA ထပ်ခါတလဲလဲတိုင်းတာခြင်းအတွက် ပါရာမက်ထရစ်မဟုတ်သော အခြားရွေးချယ်စရာတစ်ခုဖြစ်သည်။ အုပ်စုတစ်ခုစီတွင် တူညီသောဘာသာရပ်များပေါ်လာသည့် အုပ်စုသုံးစု သို့မဟုတ် ထို့ထက်ပိုသောအုပ်စုများ၏နည်းလမ်းများကြားတွင် ကိန်းဂဏန်းအချက်အလတ်သိသာထင်ရှားသောခြားနားချက်ရှိမရှိ ဆုံးဖြတ်ရန် ၎င်းကိုအသုံးပြုသည်။

ဤသင်ခန်းစာသည် Excel တွင် Friedman စာမေးပွဲကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- Excel တွင် Friedman စာမေးပွဲ

Excel တွင် Friedman စမ်းသပ်မှုကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို လိုက်နာပါ။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

မတူညီသောဆေးဝါးသုံးမျိုးကို သောက်သုံးနေသည့် လူနာ ၁၀ ဦး၏ တုံ့ပြန်မှုအချိန် (စက္ကန့်ပိုင်းအတွင်း) ကိုပြသသည့် အောက်ပါအချက်အလက်များကို ထည့်သွင်းပါ။ လူနာတစ်ဦးစီသည် ဆေးဝါးသုံးမျိုးမှ တစ်ခုစီကို တိုင်းတာသောကြောင့်၊ ဆေးဝါးများကြား ပျမ်းမျှတုံ့ပြန်မှုအချိန်ကွာခြားခြင်းရှိမရှိ ဆုံးဖြတ်ရန် Friedman test ကို အသုံးပြုပါမည်။

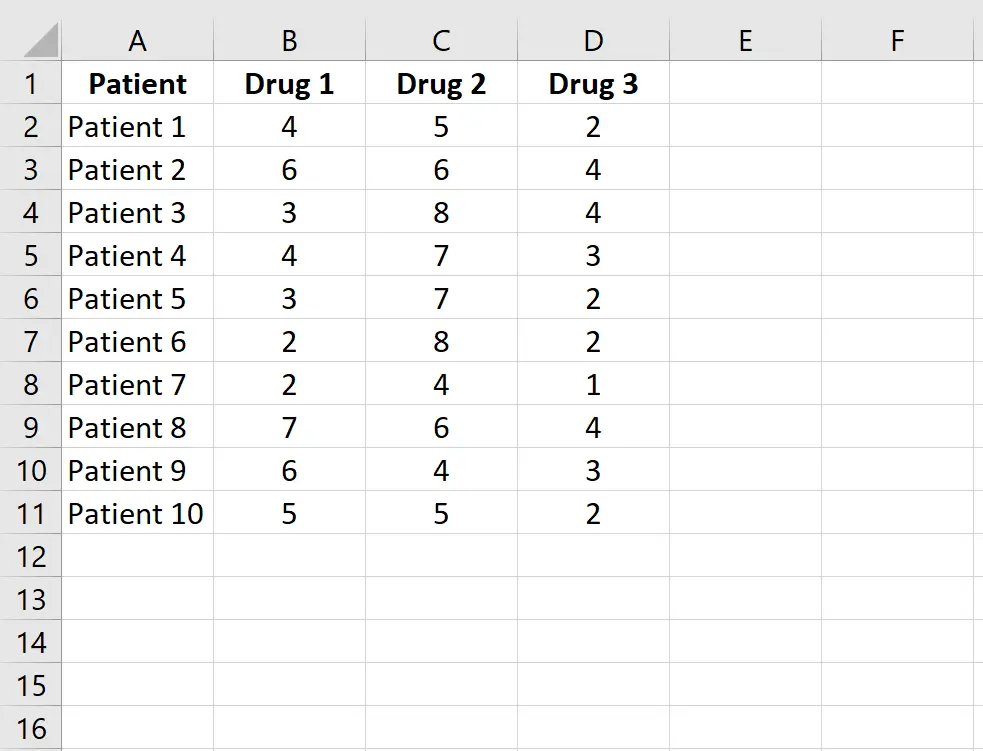
အဆင့် 2: ဒေတာကို အမျိုးအစားခွဲပါ။

ထို့နောက် =RANK.AVG() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ အတန်းတစ်ခုစီရှိ ဒေတာတန်ဖိုးများကို ငယ်စဉ်ကြီးလိုက် အဆင့်သတ်မှတ်ပါ။ အောက်ပါဖော်မြူလာသည် ဆေး 1 ကို လူနာ 1 ၏တုံ့ပြန်မှုအချိန်ကို တွက်ချက်နည်းကို ပြသသည်-

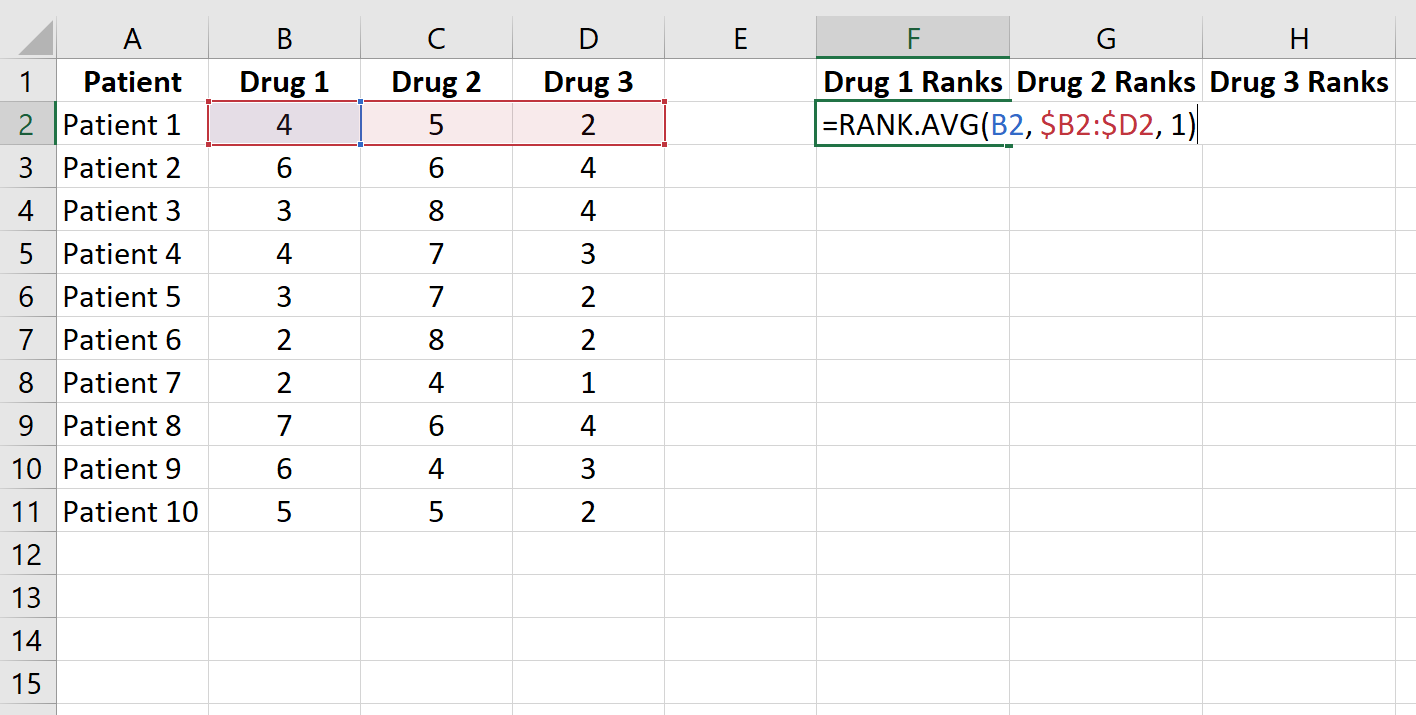
ဤဖော်မြူလာကို ကျန်ဆဲလ်များသို့ ကူးယူပါ-

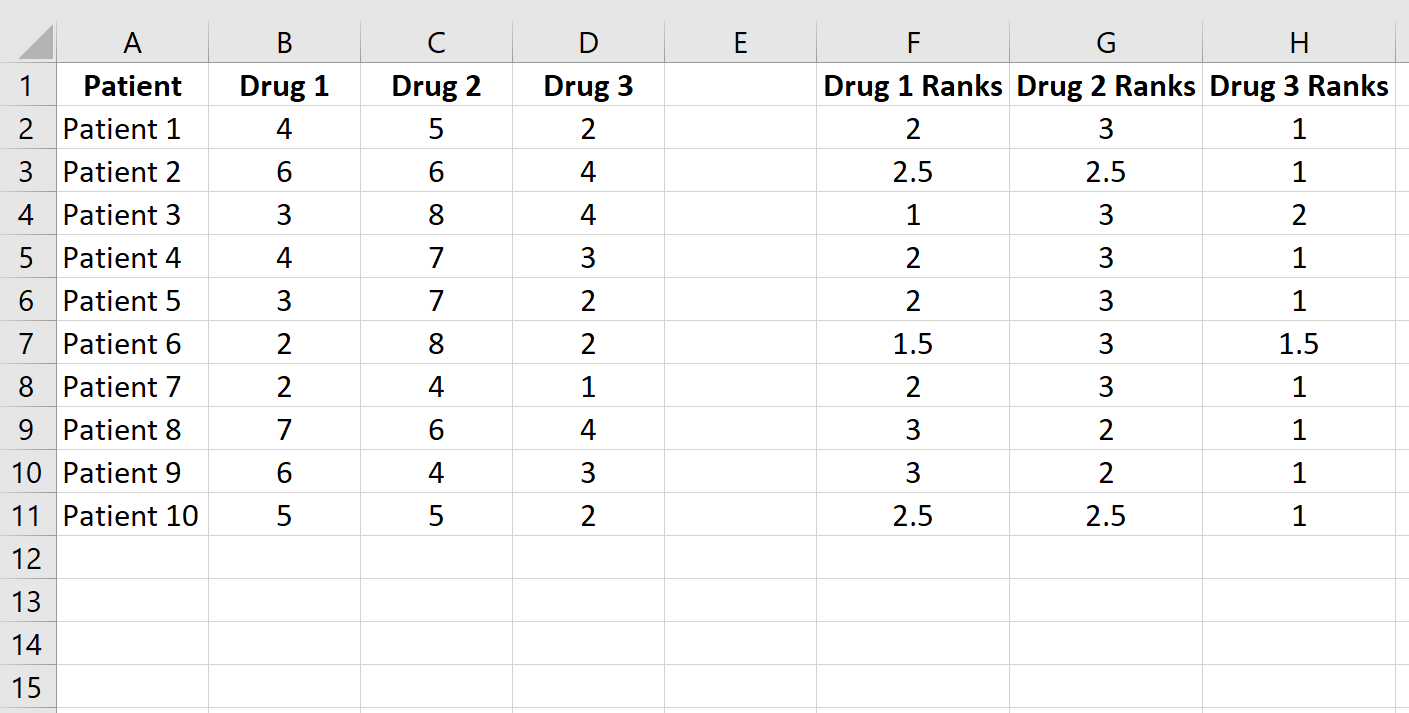
ထို့နောက်၊ ကော်လံတစ်ခုစီအတွက် အဆင့်များပေါင်းလဒ်နှင့် အဆင့်များ၏ နှစ်ထပ်ကိန်းပေါင်းကို တွက်ချက်ပါ-

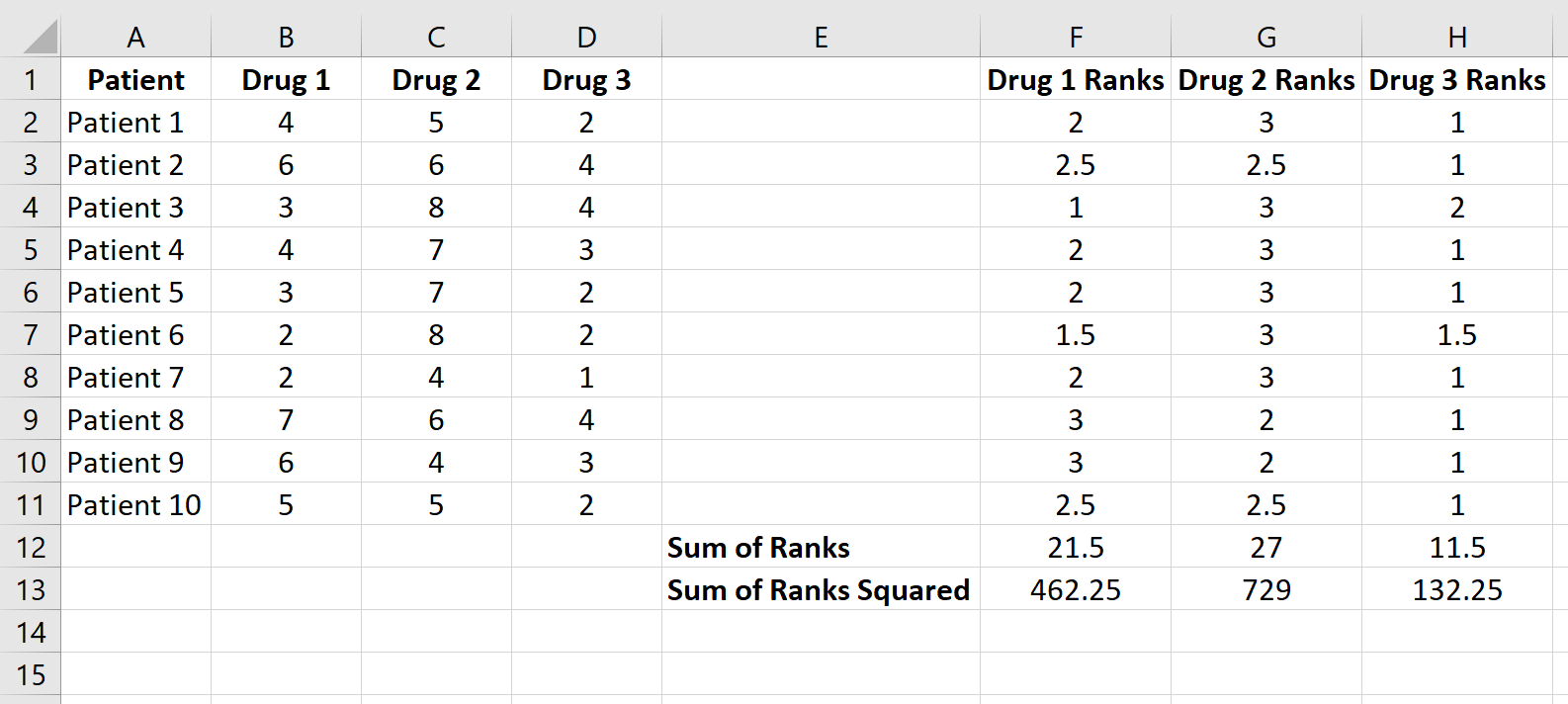
အဆင့် 3- စမ်းသပ်စာရင်းအင်းနှင့် သက်ဆိုင်ရာ p-value ကို တွက်ချက်ပါ။

စစ်ဆေးမှုစာရင်းအင်းကို အောက်ပါအတိုင်း သတ်မှတ်သည်။

Q = 12/nk(k+1) * ΣR _j ² – 3n(k+1)

ရွှေ-

• n = လူနာအရေအတွက်
• k = ကုသမှုအုပ်စုအရေအတွက်
• R _j ² = ^jth အုပ်စုအတွက် အဆင့်များ ပေါင်းခြင်း။

null hypothesis အောက်တွင်၊ Q သည် လွတ်လပ်မှု k-1 ဒီဂရီဖြင့် chi-square ဖြန့်ဖြူးမှုကို လိုက်နာသည်။

အောက်ပါ screenshot သည် စမ်းသပ်စာရင်းအင်း၊ Q နှင့် သက်ဆိုင်ရာ p-value ကို တွက်ချက်ရန် အသုံးပြုသည့် ဖော်မြူလာများကို ပြသသည်-

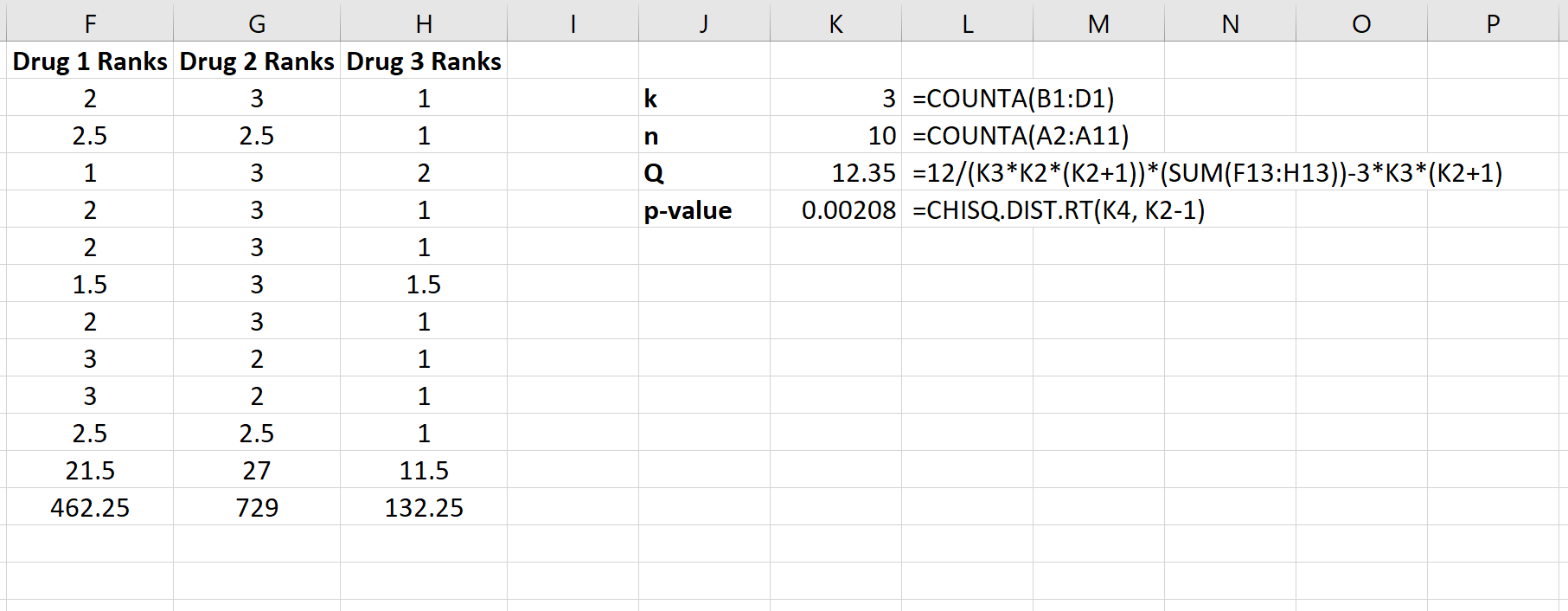
စမ်းသပ်စာရင်းအင်းသည် Q = 12.35 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value မှာ p = 0.00208 ဖြစ်သည်။ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ဆေးဝါးသုံးမျိုးလုံးအတွက် ပျမ်းမျှတုံ့ပြန်ချိန်သည် တူညီသည်ဟူသော null hypothesis ကို ငြင်းပယ်နိုင်ပါသည်။ အသုံးပြုသည့်ဆေးဝါးအမျိုးအစားသည် တုံ့ပြန်မှုအချိန်အတွင်း ကိန်းဂဏန်းအချက်အလတ်ပိုင်းခြားနားချက်များကို ဖြစ်ပေါ်စေကြောင်း ကောက်ချက်ချရန် လုံလောက်သောအထောက်အထားရှိသည်။

အဆင့် 4- ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးအနေနဲ့ စာမေးပွဲရလဒ်တွေကို အစီရင်ခံချင်ပါတယ်။ ဤသည်မှာ ဤအရာကို ပြုလုပ်ပုံ၏ ဥပမာတစ်ခုဖြစ်သည်။

Friedman test သည် လူနာ ၁၀ ဦးတွင် တုံ့ပြန်ချိန်ပေါ် မတူညီသော ဆေးဝါးသုံးမျိုး၏ အကျိုးသက်ရောက်မှုကို စစ်ဆေးရန် ပြုလုပ်ခဲ့သည်။ လူနာတစ်ဦးစီသည် ဆေးတစ်ကြိမ်စီသုံးသည်။

ရလဒ်များက အသုံးပြုသော ဆေးအမျိုးအစားသည် တုံ့ပြန်ချိန်အတွင်း ကိန်းဂဏန်းသိသိသာသာ ကွဲပြားမှုများ ဖြစ်ပေါ်ခဲ့သည် (Q = 12.35၊ p = 0.00208)။