Gamma ဖြန့်ဖြူးခြင်း။

အားဖြင့် Benjamin Anderson ဩဂုတ် 3, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် gamma ဖြန့်ဖြူးမှုမှာ အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့ကြောင့်၊ gamma ဖြန့်ဖြူးမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ ၎င်း၏ဂုဏ်သတ္တိများနှင့် ၎င်း၏ဂရပ်ဖစ်ကိုယ်စားပြုပုံသဏ္ဍာန်တို့ကို သင်တွေ့လိမ့်မည်။

ဂမ်မာဖြန့်ဖြူးမှုဆိုတာဘာလဲ။

gamma ဖြန့်ဖြူးမှုသည် α နှင့် λ တို့၏ လက္ခဏာရပ်ဘောင်နှစ်ခုဖြင့် သတ်မှတ်ထားသော ဆက်တိုက်ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။ တစ်နည်းဆိုရသော်၊ gamma ဖြန့်ဝေမှုသည် ၎င်း၏ ကန့်သတ်ဘောင်နှစ်ခု၏ တန်ဖိုးပေါ်တွင် မူတည်သည်- α သည် ပုံသဏ္ဍာန် ဘောင်ဖြစ်ပြီး λ သည် အတိုင်းအတာ ကန့်သတ်ချက်ဖြစ်သည်။

gamma ဖြန့်ဖြူးမှုအတွက် သင်္ကေတသည် ဂရိစာလုံး Γ ဖြစ်သည်။ ထို့ကြောင့် ကျပန်း variable သည် gamma ဖြန့်ဝေမှုကို လိုက်နာပါက၊ ၎င်းကို အောက်ပါအတိုင်း ရေးသားထားသည်။

$X\sim \Gamma(\alpha,\lambda)$

ပုံသဏ္ဍာန်ဘောင် k = α နှင့် ပြောင်းပြန်စကေး ဘောင် θ = 1/λ တို့ကို အသုံးပြု၍ ဂမ်မာဖြန့်ဖြူးမှုကိုလည်း ကန့်သတ်သတ်မှတ်နိုင်သည်။ ကိစ္စရပ်တိုင်းတွင်၊ gamma ဖြန့်ဖြူးမှုကို သတ်မှတ်သည့် ဘောင်နှစ်ခုသည် အပြုသဘောဆောင်သော ကိန်းဂဏန်းများဖြစ်သည်။

ပုံမှန်အားဖြင့်၊ ဂရပ်ဖစ်၏ ဘယ်ဘက်ခြမ်းရှိ ဒေတာများ ပိုမိုစူးစိုက်မှုရှိစေရန် ညာဘက်မှစောင်းနေသော ဒေတာအတွဲများကို ပုံစံထုတ်ရန်အတွက် gamma ဖြန့်ဖြူးမှုကို အသုံးပြုသည်။ ဥပမာအားဖြင့်၊ ဂမ်မာဖြန့်ဖြူးမှုကို လျှပ်စစ်အစိတ်အပိုင်းများ၏ ယုံကြည်စိတ်ချရမှုကို နမူနာယူရန် အသုံးပြုသည်။

Gamma ဖြန့်ဖြူးမှု ပုံကြမ်း

gamma ဖြန့်ဖြူးမှု၏ဂရပ်သည် ၎င်း၏ဝိသေသဘောင်များတန်ဖိုးများပေါ်တွင်မူတည်သည်။ ပုံသဏ္ဍာန်ဘောင်နှင့် စကေးပါရာမီတာပေါ်မူတည်၍ ဂမ်မာဖြန့်ဖြူးမှု၏သိပ်သည်းဆလုပ်ဆောင်ပုံကို အောက်တွင် ကြည့်ရှုနိုင်ပါသည်။

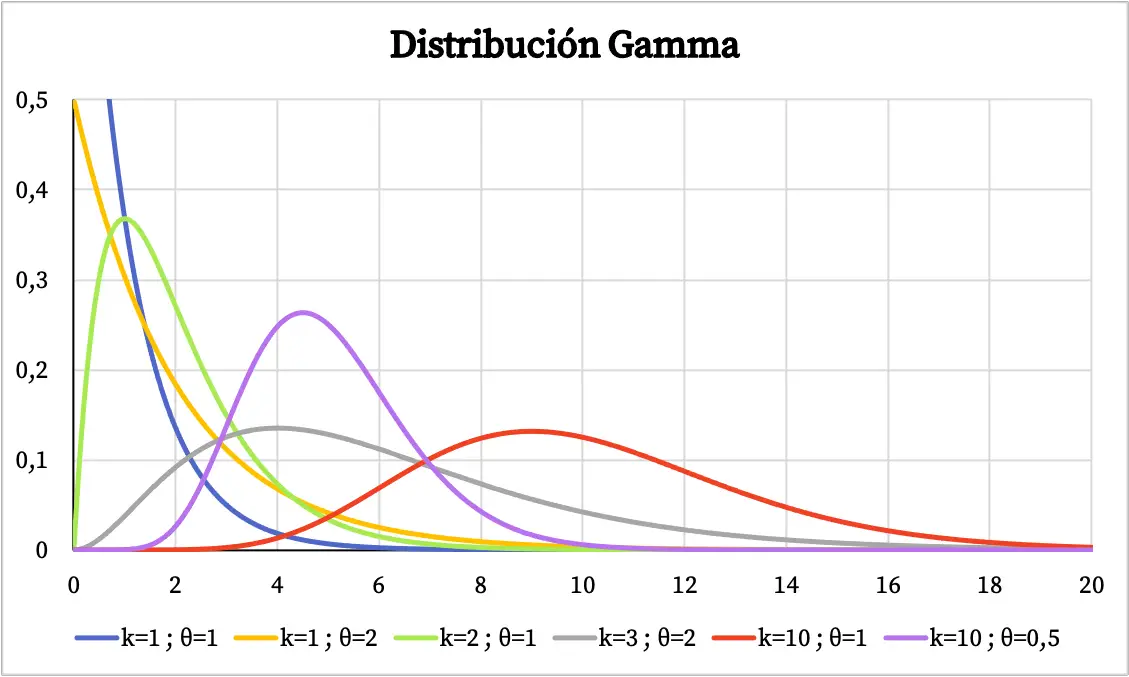
အခြားတစ်ဖက်တွင်၊ အောက်ဖော်ပြပါ gamma ဖြန့်ဖြူးမှု၏ စုစည်းဖြစ်နိုင်ခြေဆိုင်ရာ ဂရပ်ကို သင်တွေ့မြင်နိုင်သည်-

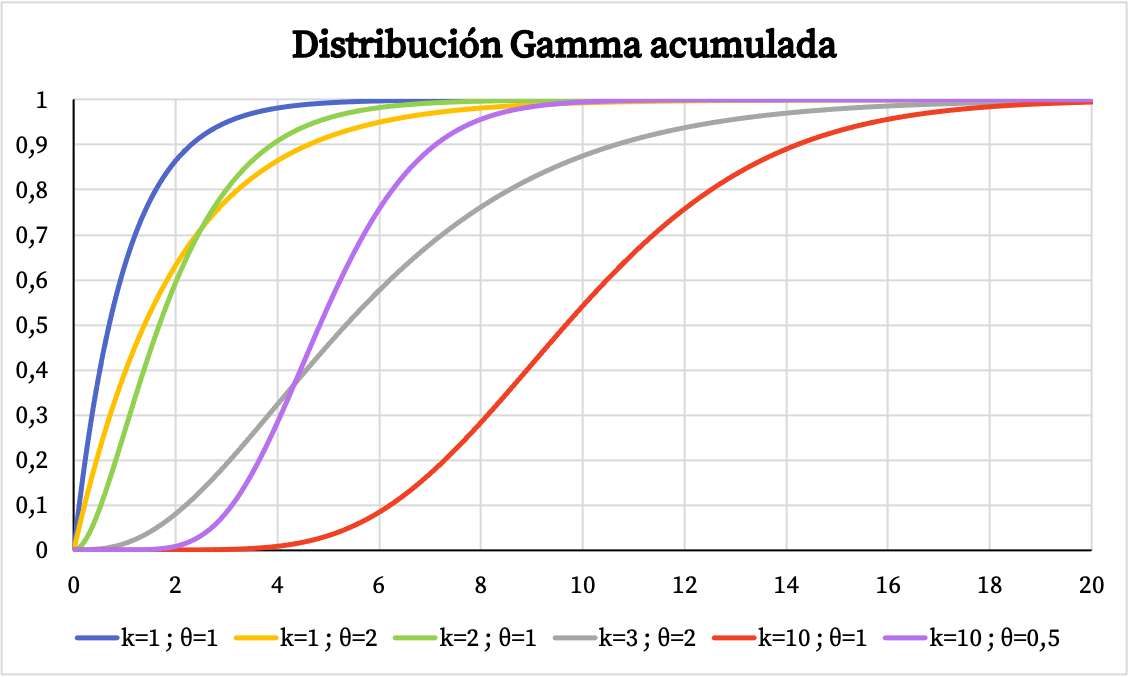
Gamm ဖြန့်ဖြူးမှု၏ စုစည်းဖြစ်နိုင်ခြေ လုပ်ဆောင်ချက်၏ ဂရပ်

ဂမ်မာဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

ထို့နောက် ဂမ်မာဖြန့်ဖြူးခြင်း၏ လက္ခဏာရပ်များကို ကြည့်ပါမည်။

gamma ဖြန့်ဝေမှု၏ ဂရပ်ကို ၎င်း၏ လက္ခဏာ ဘောင်နှစ်ခုဖြင့် လုံးလုံးလျားလျား သတ်မှတ်သည်- α သည် ပုံသဏ္ဍာန် ဘောင်နှင့် λ သည် အတိုင်းအတာ ကန့်သတ်ချက် ဖြစ်သည်။

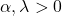
$\alpha , \lambda >0″ title=” Rendered by QuickLaTeX.com” height=” 16″ width=” 62″ style=” vertical-align: -4px;” ></p> </p> <ul> <li> ဂမ်မာဖြန့်ဖြူးမှု၏ ဒိုမိန်းကို အပြုသဘောဆောင်သော ဂဏန်းများဖြင့်သာ ဖွဲ့စည်းထားသည်။</li> </ul> <p class=$ $x\in (0,+\infty)$

ဂမ်မာဖြန့်ဖြူးမှု၏ပျမ်းမျှသည် ပုံသဏ္ဍာန်ဘောင်နှင့် စကေးကန့်သတ်ဘောင်ကြားရှိ အချိုးအစားဖြစ်သည့် α/λ ဖြစ်သည်။

$E[X]=\cfrac{\alpha}{\lambda}$

gamma ဖြန့်ဖြူးမှု၏ကွဲလွဲမှုသည် စကေးပါရာမီတာ၏ နှစ်ထပ်ကိန်းဖြင့် ပိုင်းခြားထားသော ပုံသဏ္ဍာန်ဘောင်နှင့် ညီမျှသည်။

$Var(X)=\cfrac{\alpha}{\lambda^2}$

1 ထက်နည်းသော α တန်ဖိုးများအတွက်၊ မုဒ်သည် 0 ဖြစ်သည်။ သို့သော် α သည် 1 နှင့် ညီမျှခြင်း သို့မဟုတ် ကြီးပါက၊ gamma ဖြန့်ဖြူးမှုမုဒ်ကို အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်နိုင်သည်-

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

gamma ဖြန့်ဖြူးမှု၏ သိပ်သည်းဆလုပ်ဆောင်မှုအတွက် ဖော်မြူလာမှာ-

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Γ သည် gamma function ဖြစ်ပြီး၊

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

ဂမ်မာဖြန့်ဖြူးမှုဖြင့်သတ်မှတ်ထားသော ကျပန်းကိန်းရှင်တစ်ခု၏ စုစည်းဖြန့်ဝေမှုအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်-

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

ပုံသဏ္ဍာန်ဘောင် α သည် 1 နှင့် ညီမျှပါက၊ ထို့နောက် ဂမ်မာဖြန့်ဝေမှုသည် တူညီသောစကေးပါရာမီတာ λ ရှိသော ထပ်ကိန်းခွဲဝေမှုတစ်ခုနှင့် ညီမျှသည်။

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

စကေးပါရာမီတာ λ သည် ပျမ်းမျှဖြစ်သောအခါ၊ gamma ဖြန့်ဝေမှုသည် chi-square ဖြန့်ဖြူးမှု ၏ အထူးကိစ္စရပ်ဖြစ်သည်။

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။

ဂမ်မာဖြန့်ဖြူးမှုဆိုတာဘာလဲ။

Gamma ဖြန့်ဖြူးမှု ပုံကြမ်း

ဂမ်မာဖြန့်ဖြူးခြင်း၏လက္ခဏာများ

စာရေးသူအကြောင်း

Benjamin Anderson

မှတ်ချက်တစ်ခုထည့်ပါ။