Gini အညွှန်းကိန်း (သို့မဟုတ် gini coefficient)

ဤဆောင်းပါးတွင် Gini အညွှန်းကိန်းကို Gini coefficient ဟုလည်းခေါ်ပြီး ၎င်းကိုအသုံးပြုသည့်အရာအား ရှင်းပြထားသည်။ ထို့အပြင်၊ Gini အညွှန်းကိန်းကိုရှာဖွေနည်းကိုဖြေရှင်းထားသောလေ့ကျင့်ခန်းကိုသင်တွေ့လိမ့်မည်။ နောက်ဆုံးတွင်၊ ဤစာရင်းအင်းမက်ထရစ်၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်နှင့် Gini အညွှန်းကိန်းနှင့် Lorenz မျဉ်းကွေးကြားရှိဆက်ဆံရေးကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။

Gini အညွှန်းကိန်းကဘာလဲ။

Gini အညွှန်းကိန်း ( Gini coefficient) သည် နယ်မြေတစ်ခု၏ ၀င်ငွေမညီမျှမှုကို တိုင်းတာရန်အတွက် အသုံးပြုသည့် ကိန်းဂဏန်းတန်ဖိုးတစ်ခုဖြစ်သည်။ တစ်နည်းဆိုရသော် Gini အညွှန်းကိန်းသည် ၎င်း၏လူဦးရေအကြား ဝင်ငွေခွဲဝေမှုတွင် နယ်မြေတစ်ခု မည်မျှ ညီမျှသည်ကို ဖော်ပြသည်။

Gini အညွှန်းကိန်းသည် 0 နှင့် 1 အကြားရှိ နံပါတ်တစ်ခုဖြစ်သည်။ Gini အညွှန်းကိန်းသည် 0 ဖြစ်ပါက၊ ဆိုလိုသည်မှာ ရပ်ကွက်အတွင်း ဝင်ငွေခွဲဝေမှုသည် တတ်နိုင်သမျှ မျှမျှတတ (ပြီးပြည့်စုံသော တန်းတူညီမျှမှု) သို့မဟုတ် တစ်နည်းအားဖြင့် နေထိုင်သူအားလုံးတွင် တူညီသောဝင်ငွေရှိသည်။ အခြားတစ်ဖက်တွင်၊ Gini coefficient သည် 1 ဖြစ်သောအခါ၊ ၎င်းသည် ပြီးပြည့်စုံသောမညီမျှမှုနှင့် သက်ဆိုင်သည်၊ ဆိုလိုသည်မှာ လူတစ်ဦးသည် ရပ်ကွက်၏ ၀င်ငွေအားလုံးရှိပြီး အခြားသူများမှာ ဘာမျှမရရှိဟု ဆိုလိုသည်။

Gini အညွှန်းကိန်းကို သာတူညီမျှဆုံးနိုင်ငံများနှင့် နှိုင်းယှဉ်ပါက ဝင်ငွေခွဲဝေမှုအရ တန်းတူညီမျှမှုအရှိဆုံးနိုင်ငံများကို နှိုင်းယှဉ်ရန်ဖြစ်နိုင်သောကြောင့် ကမ္ဘာပေါ်ရှိ ကွဲပြားခြားနားသောနိုင်ငံများအကြား စီးပွားရေးအခြေအနေကို နှိုင်းယှဉ်ရန်အတွက် အသုံးပြုပါသည်။

Gini အညွှန်းကိန်းကို နာမည်ကျော် စာရင်းအင်းပညာရှင် Corrado Gini မှ တီထွင်ခဲ့ခြင်းကြောင့် ၎င်း၏အမည်ကို ရရှိခဲ့သည်။

Gini အညွှန်းကိန်းဘယ်လိုတွက်ရမလဲ

Gini အညွှန်းကိန်း (သို့မဟုတ် Gini coefficient) ၏အဓိပ္ပာယ်ဖွင့်ဆိုချက်သည် ဤစာရင်းအင်းတိုင်းတာမှုအား တွက်ချက်ပုံဖြစ်သည်။

Gini အညွှန်းကိန်း (သို့မဟုတ် Gini coefficient) အတွက် ဖော်မြူလာ မှာ အောက်ပါအတိုင်းဖြစ်သည်-

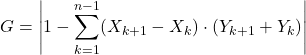
ရွှေ-

• 

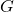
  Gini အညွှန်းကိန်းဖြစ်သည်။

• 

  ပြောင်းလဲနိုင်သော လူဦးရေ၏ တိုးပွားလာသော အချိုးအစားဖြစ်သည်။

• 

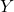
  ဝင်ငွေကိန်းဂဏန်းသည် ပြောင်းလဲနိုင်သော အချိုးအစားဖြစ်သည်။

Gini အညွှန်းကို မည်သို့ဆုံးဖြတ်သည်ကို အတိအကျမြင်နိုင်စေရန်၊ အောက်တွင် အဆင့်ဆင့် ဥပမာကို ဖြေရှင်းပြီးပါပြီ-

• အောက်ပါဇယားတွင်ဖော်ပြထားသောဝင်ငွေရှိသောလူဦးရေ၏ Gini အညွှန်းကိုတွက်ချက်ပါ။

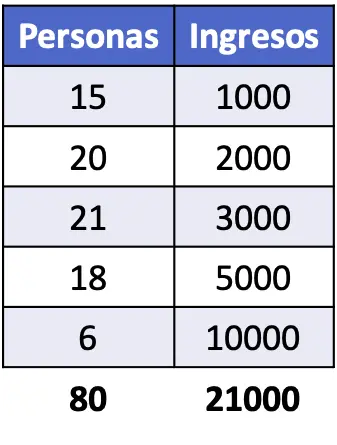
Gini coefficient ကိုရှာရန်အတွက်၊ ကျွန်ုပ်တို့သည် ဝင်ငွေအဆင့်တစ်ခုစီ၏အချိုးအစားနှင့် တိုးပွားလာသောအချိုးအစားကို ဆုံးဖြတ်ရန် လိုအပ်ပါသည်။ ထို့အပြင်၊ ဖော်မြူလာတွင်ပေးထားသော တွက်ချက်မှုများကို Gini အညွှန်းကိန်း၏တန်ဖိုးကိုရှာဖွေရန် လုပ်ဆောင်ရမည်ဖြစ်သည်။

အတိုချုပ်အားဖြင့်၊ အောက်ပါကော်လံများကို ဒေတာဇယားသို့ ထည့်သင့်သည်-

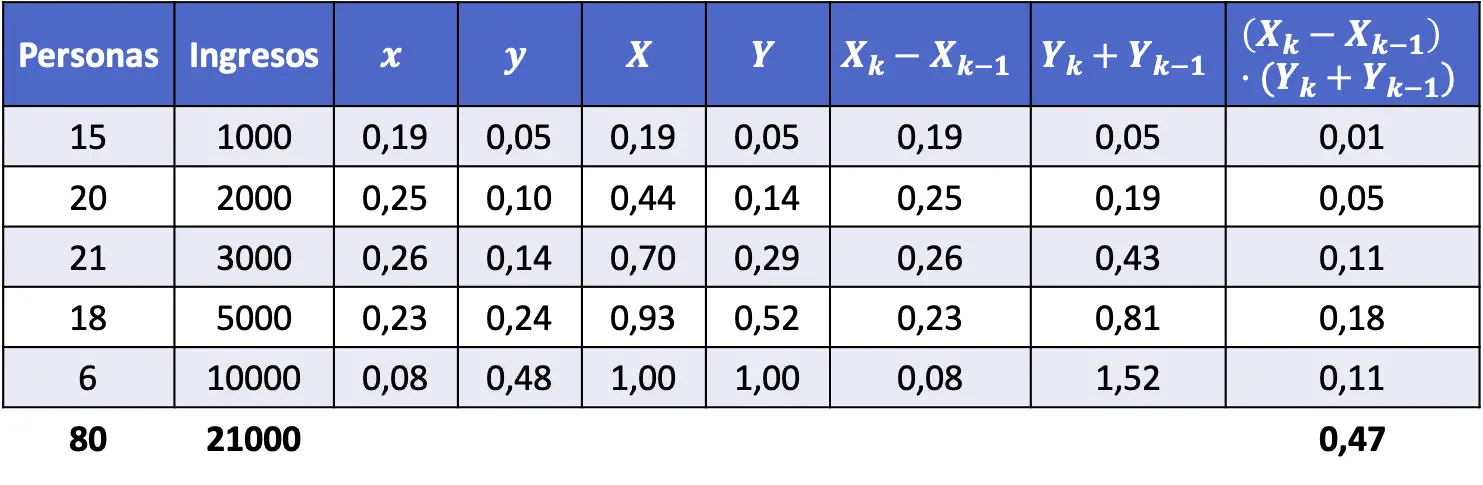
ယခု ကျွန်ုပ်တို့သည် Gini အညွှန်းကိန်းဖော်မြူလာကို အသုံးပြုသည်-

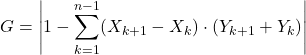
နောက်ဆုံးအနေနှင့်၊ ကျွန်ုပ်တို့သည် ဒေတာကို အက္ခရာသင်္ချာအညွှန်းဖြင့် အစားထိုးပြီး Gini coefficient ကို တွက်ချက်သည်-

Gini အညွှန်းကိန်းနှင့် Lorenz မျဉ်းကွေးကြား ဆက်စပ်မှု

ဤအပိုင်းတွင်၊ Gini အညွှန်းကိန်း၊ Gini coefficient ဟုလည်းလူသိများသော၊ နှင့် Lorenz မျဉ်းကွေးတို့ မည်သို့ဆက်စပ်သည်ကို ကျွန်ုပ်တို့ကြည့်ရှုပါမည်။

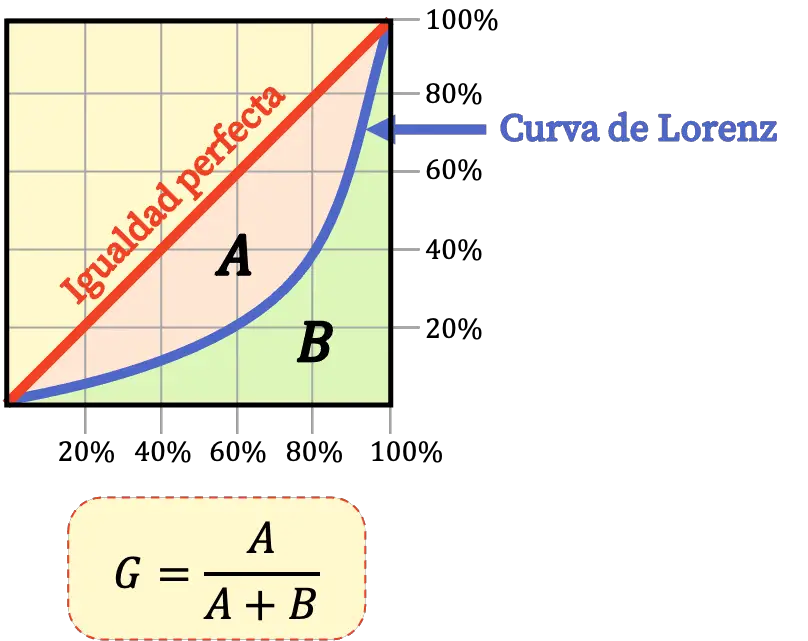
Lorenz မျဉ်းကွေး သည် နယ်မြေတစ်ခု၏ လူဦးရေ၏ စီးပွားရေးမညီမျှမှုများကို ဂရပ်ဖစ်ဖော်ပြသည်။ ထို့ကြောင့် Lorenz မျဉ်းကွေးသည် လူဦးရေ၏ စီးပွားရေးမညီမျှမှုကို အမြင်အားဖြင့် ညွှန်ပြသည်။

အခြားတစ်ဖက်တွင်၊ ကျွန်ုပ်တို့မြင်ခဲ့ရသည့်အတိုင်း၊ Gini အညွှန်းကိန်းသည် လူဦးရေ၏မညီမျှမှုများကို ကိန်းဂဏာန်းဖော်ပြရန် အသုံးပြုသည့်တန်ဖိုးတစ်ခုဖြစ်သည်။

ထို့ကြောင့် Gini အညွှန်းကိန်းနှင့် Lorenz မျဉ်းကွေးသည် တူညီသော ရည်ရွယ်ချက် ရှိသည် – နှစ်ခုလုံးကို နယ်မြေအတွင်း နေထိုင်သူများအကြား စီးပွားရေးမညီမျှမှုများကို ဆုံးဖြတ်ရန် အသုံးပြုသည်။ သို့သော်၊ Gini အညွှန်းကိန်းသည် ဝင်ငွေမညီမျှမှုကို ကိန်းဂဏန်းများဖြင့် အကဲဖြတ်ပြီး Lorenz မျဉ်းကွေးသည် စီးပွားရေးမညီမျှမှုကို ဂရပ်ဖစ်ဖြင့် ပိုင်းခြားထားသည်။

ထို့အပြင်၊ Gini အညွှန်းကိန်းကို အောက်ပါဖော်မြူလာအရ Lorenz မျဉ်းကွေးဖြင့် ကန့်သတ်ထားသော ဧရိယာများမှ တွက်ချက်နိုင်သည်-

Gini အညွှန်းကိန်း၏စကားပြန်

Gini အညွှန်းကိန်း၏တန်ဖိုးသည် 0 မှ 1 အထိ၊ နှစ်ခုလုံးပါဝင်နိုင်သည်။ Gini coefficient ၏တန်ဖိုးသည် 0 နှင့် ပိုနီးစပ်လေ၊ ဆိုလိုသည်မှာ နယ်မြေတွင် စီးပွားရေးအရ တန်းတူညီမျှမှု ပိုရှိလာခြင်းဖြစ်သည်။ အခြားတစ်ဖက်တွင်၊ Gini အညွှန်းကိန်းတန်ဖိုး မြင့်မားလေ၊ ရပ်ကွက်တစ်ခု၏မြို့သူမြို့သားများအကြား ဝင်ငွေခွဲဝေမှုတွင် မညီမျှမှုများ ပိုများလာလေဖြစ်သည်။

ထို့ကြောင့် Gini အညွှန်းကိန်းသည် မြို့သူမြို့သားအားလုံး အတိအကျတူညီသော ဝင်ငွေရှိသည့် အကောင်းဆုံးအခြေအနေတွင် သုညနှင့် ညီမျှမည်ဖြစ်သည်။ ဆန့်ကျင်ဘက်အနေနှင့်၊ နယ်မြေသည် ပြီးပြည့်စုံသောမညီမျှမှုကိုတင်ပြသောအခါတွင် Gini အညွှန်းကိန်းသည် 1 နှင့်တန်ဖိုးရှိလိမ့်မည်၊ ဆိုလိုသည်မှာ မြို့သူမြို့သားတစ်ဦးသည် ဝင်ငွေအားလုံးကိုရရှိပြီး ကျန်နေထိုင်သူများမှာ ဝင်ငွေမရှိဟုဆိုလိုသည်။

ထို့ကြောင့် ဝင်ငွေ တန်းတူညီမျှသော နိုင်ငံများသည် Gini အညွှန်းကိန်း နိမ့်ကျသူများ ဖြစ်သည်။ မညီမျှဆုံးနိုင်ငံများတွင် အလွန်မြင့်မားသော Gini အညွှန်းကိန်းရှိသည်။

ကျွန်ုပ်တို့မြင်ခဲ့သည့်အတိုင်း၊ Gini အညွှန်းသည် Lorenz မျဉ်းကွေးနှင့် ချိတ်ဆက်ထားသည်။ ထို့ကြောင့်၊ Gini အညွှန်းကိန်းနိမ့်လေ၊ Lorenz မျဉ်းကွေးသည် ပြီးပြည့်စုံသော တန်းတူညီမျှမှုမျဉ်းသို့ နီးကပ်လေဖြစ်သည်။ Gini အညွှန်းကိန်း မြင့်နေချိန်တွင်၊ Gini မျဉ်းကွေးသည် ကွေးညွှတ်မှု ပိုများလာမည်ဖြစ်ပြီး ထို့ကြောင့်၊ ပြီးပြည့်စုံသော တန်းတူညီမျှမှုကို ကိုယ်စားပြုသည့် မျဉ်းကြောင်းမှ ပိုမိုများပြားလာမည်ဖြစ်သည်။