Histograms များကို နှိုင်းယှဉ်နည်း (ဥပမာများနှင့်)

ဟီစတိုဂရမ် ဆိုသည်မှာ ဒေတာအစုတစ်ခုတွင် တန်ဖိုးများ ဖြန့်ဖြူးမှုကို မြင်သာအောင် မြင်နိုင်စေသည့် ဇယားအမျိုးအစားတစ်ခုဖြစ်သည်။

X-axis သည် dataset ၏တန်ဖိုးများကိုပြသပြီး Y-axis သည်တန်ဖိုးတစ်ခုစီ၏ကြိမ်နှုန်းကိုပြသသည်။

Histograms များသည် ဒေတာအစုံတွင် တန်ဖိုးများ ဖြန့်ဝေမှုကို လျင်မြန်စွာ နားလည်နိုင်သောကြောင့် ၎င်းတို့သည် အသုံးဝင်ပါသည်။ ၎င်းတို့သည် မတူညီသော ဒေတာအတွဲနှစ်ခုကို နှိုင်းယှဉ်ရန်အတွက်လည်း အသုံးဝင်ပါသည်။

နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ဟီစတိုဂရမ်များကို နှိုင်းယှဉ်သောအခါ၊ ကျွန်ုပ်တို့သည် မတူညီသော မေးခွန်းသုံးခုကို ဖြေနိုင်သည်-

1. အလယ်အလတ်တန်ဖိုးများကို မည်သို့နှိုင်းယှဉ်သနည်း။

ဖြန့်ဖြူးမှု၏ ပျမ်းမျှတန်ဖိုးများကို နှိုင်းယှဉ်နိုင်စေမည့် ပျမ်းမျှသည် ဟီစတိုဂရမ်တစ်ခုစီ၏ အလယ်အနီးတွင် ရှိနေကြောင်း အကြမ်းဖျင်း ခန့်မှန်းနိုင်သည်။

2. ပြန့်ကျဲမှု မည်ကဲ့သို့ နှိုင်းယှဉ်သနည်း။

ဘယ် Histogram က ပိုပြန့်ကားသလဲဆိုတာကို ကျွန်ုပ်တို့ မြင်သာထင်သာမြင်နိုင်ပြီး၊ ဘယ်ဖြန့်ဖြူးမှုမှာ ပိုကွဲကွာတဲ့တန်ဖိုးတွေရှိလဲဆိုတဲ့ အတွေးအမြင်ကို ပေးစွမ်းနိုင်ပါတယ်။

3. အချိုးမညီမှုကို မည်သို့နှိုင်းယှဉ်သနည်း။

ဟစ်စတိုဂရမ်တစ်ခု၏ ဘယ်ဘက်အခြမ်းတွင် “ အမြီး” ပါရှိပါက၊ ၎င်းအား အနုတ်လက္ခဏာ လှည့်ပတ်သည်ဟု ဆိုသည်။ အပြန်အလှန်အားဖြင့်၊ ဟစ်စတိုဂရမ်တစ်ခုသည် ကွက်ကွက်၏ညာဘက်ခြမ်းတွင် “ အမြီး” ရှိပါက၊ ၎င်းကို အပြုသဘောဖြင့် လှည့်ကြည့်သည်ဟု ဆိုသည်။ မှုန်ဝါးခြင်း နှိုင်းယှဉ်ရန် histogram တစ်ခုစီကို အမြင်အာရုံဖြင့် စစ်ဆေးနိုင်ပါသည်။

အောက်ဖော်ပြပါ ဥပမာသည် မတူညီသော histogram နှစ်ခုကို နှိုင်းယှဉ်ပြီး ဤမေးခွန်းသုံးခုကိုဖြေဆိုနည်းကို ပြသထားသည်။

ဥပမာ- ဟစ်စတိုဂရမ်များကို နှိုင်းယှဉ်ခြင်း။

ကျောင်းသား 200 သည် စာမေးပွဲအတွက် ပြင်ဆင်ရန် လေ့လာမှုနည်းလမ်းတစ်ခုကို အသုံးပြုပြီး အခြားကျောင်းသား 200 သည် တူညီသောစာမေးပွဲအတွက် ပြင်ဆင်ရန်အတွက် မတူညီသောလေ့လာမှုနည်းလမ်းကို အသုံးပြုသည်ဟု ယူဆသည်။

ကျောင်းသားအုပ်စုတစ်ခုစီ၏ စာမေးပွဲရလဒ်များကို နှိုင်းယှဉ်ရန် အောက်ပါ ဟီစတိုဂရမ်များကို ဖန်တီးသည်ဆိုပါစို့။

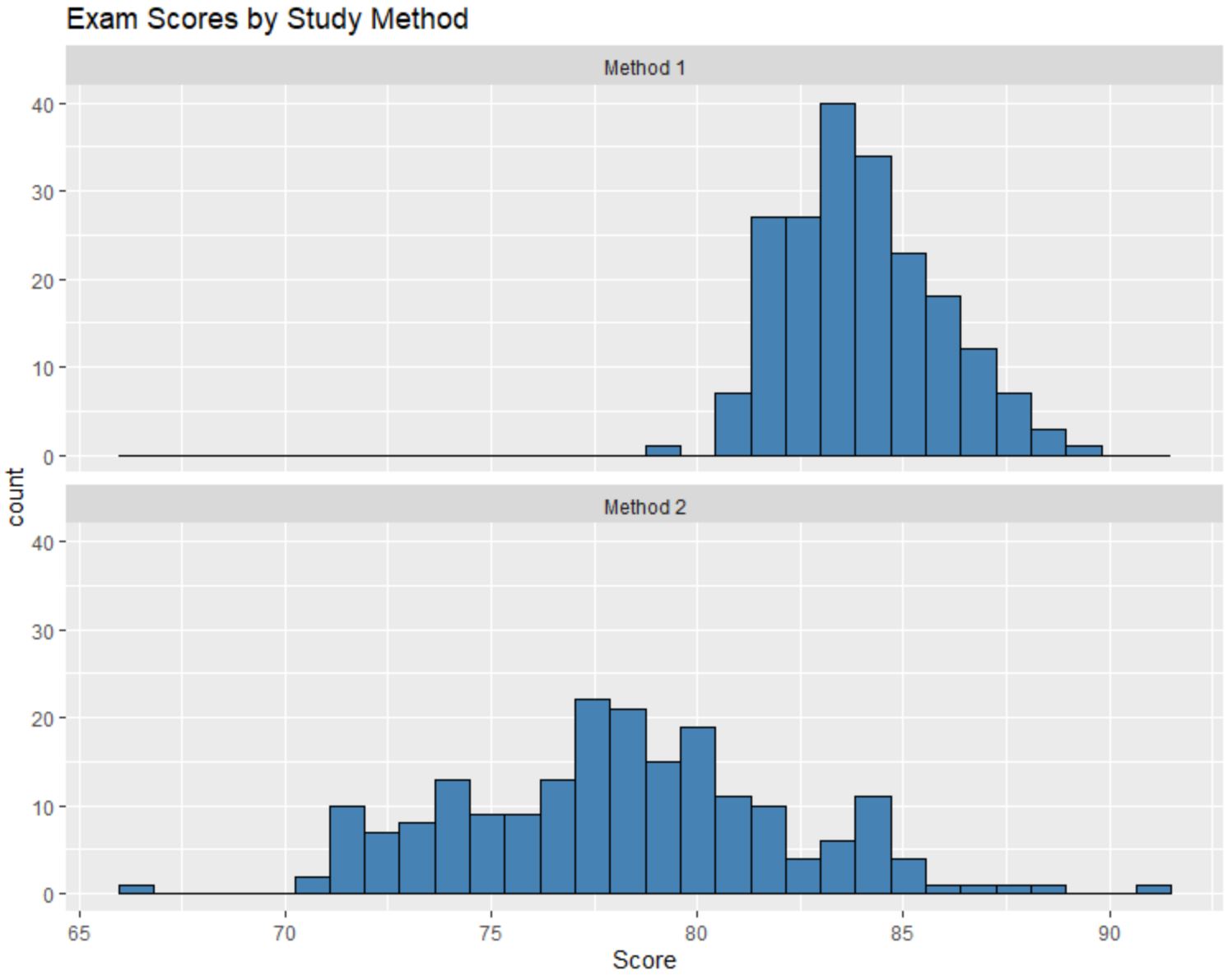
ဤဟစ်စတိုဂရမ်များကို နှိုင်းယှဉ်ပြီး အောက်ပါမေးခွန်းသုံးခုကို ဖြေနိုင်သည်-

1. အလယ်အလတ်တန်ဖိုးများကို မည်သို့နှိုင်းယှဉ်သနည်း။

ဖြန့်ဖြူးမှုတစ်ခုစီ၏ ပျမ်းမျှတန်ဖိုးများကို ကျွန်ုပ်တို့မသိသော်လည်း Method 1 ကိုအသုံးပြုသော ကျောင်းသားများ၏ ပျမ်းမျှစာမေးပွဲရမှတ်သည် Method 1 ကိုအသုံးပြုသော ကျောင်းသားများ၏ ပျမ်းမျှစာမေးပွဲရမှတ်ထက် ပိုများကြောင်း ထင်ရှားပါသည်။ နည်းလမ်း ၂။

နည်းလမ်း 1 အတွက် ပျမ်းမျှတန်ဖိုးသည် 84 ဝန်းကျင်ဖြစ်ပြီး နည်းလမ်း 2 အတွက် ပျမ်းမျှတန်ဖိုးမှာ 78 ဝန်းကျင်ဖြစ်ကြောင်း ကျွန်ုပ်တို့ ခန့်မှန်းနိုင်ပါသည်။

2. ပြန့်ကျဲမှု မည်ကဲ့သို့ နှိုင်းယှဉ်သနည်း။

Method 2 အတွက် ဟီစတိုဂရမ်တန်ဖိုးများသည် Method 1 အတွက်ထက် များစွာပို၍ ကွဲလွဲနေပြီး Method 2 ကိုအသုံးပြုသော ကျောင်းသားများအတွက် စာမေးပွဲရလဒ်များတွင် ကွဲလွဲမှုများစွာ ရှိနေကြောင်း ပြောပြသည်။

3. အချိုးမညီမှုကို မည်သို့နှိုင်းယှဉ်သနည်း။

ဟီစတိုဂရမ်များကိုကြည့်လျှင် Method 1 အတွက် စာမေးပွဲရမှတ်များ ခွဲဝေမှုသည် ဟီစတိုဂရမ်၏ ညာဘက်သို့ ဖြန့်ထားသော “ အမြီး” မှ ညွှန်ပြထားသည့်အတိုင်း ညာဘက်သို့ အနည်းငယ် စောင်းနေပုံပေါ်သည်။

သို့သော်၊ နည်းလမ်း 2 အတွက် စာမေးပွဲရလဒ်များ ဖြန့်ဝေမှုတွင် “ အမြီး” ရှိပုံမပေါ်ပါ၊ ၎င်းသည် ကျွန်ုပ်တို့အား ဖြန့်ဝေမှုသည် အနည်းငယ် သို့မဟုတ် မလွဲမသွေဖြစ်ကြောင်း ပြောပြသည်။

ဘောနပ်စ် – ဤဟစ်စတိုဂရမ်နှစ်ခုကို ဖန်တီးရန် R တွင် ကျွန်ုပ်တို့အသုံးပြုခဲ့သည့် ကုဒ်ဖြစ်ပါသည်-

 library (ggplot2)

#make this example reproducible
set. seeds (0)

#create data frame
df <- data. frame (method=rep(c(' Method 1 ', ' Method 2 '), each= 200 ),
                 Score=c(rnorm( 200 , mean= 84 , sd= 2 ),
                         rnorm( 200 , mean= 78 , sd= 4 )))

#create histogram of scores for each method
ggplot(df, aes(x=Score)) +
  geom_histogram(fill=' steelblue ', color=' black ') +
  facet_wrap(.~method, nrow= 2 ) +
  labs(title=' Exam Scores by Study Method ')

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် histograms ဖြင့် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

ဟစ်စတိုဂရမ်တစ်ခု၏ ပျမ်းမျှနှင့် ပျမ်းမျှအား ခန့်မှန်းနည်း
မည်သည့် histogram ၏ စံသွေဖည်မှုကို ခန့်မှန်းနည်း
ဟစ်စတိုဂရမ်ပုံသဏ္ဍာန်ကို ဘယ်လိုဖော်ပြမလဲ။